
- •Высшая математика конспект лекций
- •1 Курс, 2 семестр
- •Содержание
- •Тема 6 «Функции нескольких переменных» 7
- •Тема 7 «Комплексные числа. Многочлены» 13
- •Тема 8 «Неопределённый интеграл» 19
- •Тема 9 «Определенный интеграл» 38
- •Тема 10 «Приложения определенного интеграла» 43
- •Тема 11 «Дифференциальные уравнения» 48
- •Введение
- •Тематический план
- •Предел функции двух переменных.
- •Частные производные первого порядка
- •Градиент функции. Производная по направлению вектора.
- •Вопросы для самоконтроля
- •Тема 7 «Комплексные числа. Многочлены» Основные понятия
- •Действия с комплексными числами
- •Рациональные дроби. Краткие сведения из теории многочленов.
- •Рациональные дроби.
- •Вопросы для самоконтроля
- •Тема 8 «Неопределённый интеграл» Первообразная функция. Основная теорема о первообразных
- •Понятие неопределенного интеграла
- •Основные свойства неопределенного интеграла
- •Инвариантность формул интегрирования
- •Метод непосредственного интегрирования
- •Метод замены переменной (способ подстановки)
- •Интегрирование по частям
- •Интегралы от некоторых функций, содержащих квадратный трехчлен
- •Интегрирования рациональных дробей
- •Интегрирование тригонометрических функций
- •Интегрирование иррациональных функций
- •Интегралы от дифференциальных биномов
- •Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок
- •Вопросы для самоконтроля
- •Тема 9 «Определенный интеграл» Понятие определённого интеграла.
- •Основные свойства определённого интеграла.
- •Вопросы для самоконтроля
- •Тема 10 «Приложения определенного интеграла» Вычисление площадей плоских фигур
- •Вычисление объема тела
- •Обыкновенные дифференциальные уравнения 1-го порядка.
- •Условие (5) называется начальным условием.
- •Дифференциальные уравнения с разделяющимися переменными.
- •Однородные дифференциальные уравнения 1-го порядка
- •Линейные дифференциальные уравнения 1-го порядка
- •Нетрудно заметить, что уравнение (21) представляет собой уравнение с разделяющимися переменными, метод решения которого изложен в лекции 1.
- •Уравнение Бернулли Уравнением Бернулли называется уравнение вида:
- •Геометрические задачи.
- •Пример 7.
- •Решение
- •Дифференциальные уравнения высших порядков.
- •Дифференциальные уравнения высших порядков, допускающие понижение порядка
- •Решить дифференциальное уравнение:
- •Пример 10.
- •Линейные дифференциальные уравнения порядка n
- •Решение линейных неоднородных уравнений
- •Решение однородных уравнений.
- •Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами.
- •Укажем частные решения , соответствующие различным простейшим случаям специальной правой части:
- •Пример. (Задача типа 61-70).
- •Решение
- •Вопросы для самоконтроля
- •Литература
Пример 7.
Кривая проходит через точку А (2; -1) и обладает тем свойством, что угловой коэффициент касательной в любой ее точке пропорционален квадрату ординаты точки касания с коэффициентом пропорциональности равным 3. Найти уравнение этой кривой.
Решение
Пусть у = у (х) – искомое уравнения кривой. Выразим все упомянутые в задаче величины через х, у, у/. Тогда данное в условии соотношение будет представлять собой дифференциальное уравнение, из которого можно найти функцию у(х).
Пусть М (х, у) – произвольная точка искомой кривой (рис. 2).
Согласно геометрическому смыслу производной, угловой коэффициент k касательной в точке М (х, у) определяется по формуле:
k=у/(х) (37)
По условию задачи: k = 3у2. Откуда, с учетом (37) получаем следующее дифференциальное уравнение: у/ = 3у2 (38)
Уравнение
(38) представляет собой уравнение с
разделяющимися переменными. Решим его
(см. лекция 1):
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]() .
(39)
.
(39)
Так
как искомая кривая проходит через точку
А (2; -1), т.е. у (2) = -1, то подставив в общее
решение (39) уравнения (38) это начальное
условие , определим значение параметра
С:
![]()
![]() ;
;
![]() .
.
Таким
образом, уравнение искомой кривой имеет
вид:
![]() (40)
(40)
Кривая
(40) представляет собой гиперболу с
центром симметрии в точке
![]() ,
асимптотами которой служат прямые
,
асимптотами которой служат прямые
![]() и у = 0 (ось Ох).
и у = 0 (ось Ох).
Дифференциальные уравнения высших порядков.
Основные понятия
Дифференциальные уравнения высших порядков имеют большое значение в прикладных задачах. Так, например уравнения 2-го порядка – в теории колебаний, теории электрических цепей, в задачах механики.
Согласно данному в лекции 1 определению, самый общий вид обыкновенного дифференциального уравнения n – го порядка (n ≥ 2) следующий:
![]() ,
(41)
,
(41)
где F – известная функция своих аргументов;
х – независимая переменная;
у – неизвестная искомая функция, зависящая от х.
В данном курсе ограничимся рассмотрением уравнений n – го порядка, разрешенных относительно старшей производной, т.е. имеющих вид:
![]() ,
(42)
,
(42)
где f – известная функция своих аргументов.
Решением
дифференциального уравнения (42) (или
(41)) называется всякая n
– раз дифференцируемая функция
![]() ,
которая обращает указанное уравнение
в тождество (лекция 1, пример 1).
,
которая обращает указанное уравнение
в тождество (лекция 1, пример 1).
Задача Коши для дифференциального уравнения n – го порядка (n ≥ 2) состоит в том, чтобы найти решение этого уравнения, удовлетворяющее условиям:
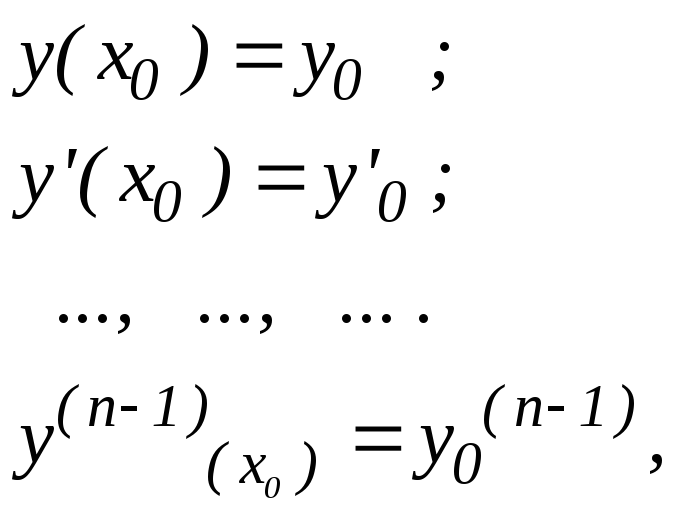 (43)
(43)
где
![]() - заданные действительные числа.
- заданные действительные числа.
Условия (43) называются начальными условиями.
Для
дифференциального уравнения 2-го порядка
начальные условия (43) имеют вид:
![]() ;
;
![]() ,
,
а геометрическая интерпретация задачи Коши заключается в следующем: среди интегральных кривых отыскать такие, которые проходят через точку М0 (х0, у0) плоскости Оху и имеют в этой точке касательную с угловым коэффициентом k равным у/0 (т.е. k = у/0).
Общим решением дифференциального уравнения n – го порядка называется n – параметрическое семейство функций:
![]() ,
(44)
,
(44)
удовлетворяющее следующим условиям:
а) при подстановке функции (44) в уравнение последнее обращается в тождество относительно х при любых допустимых значениях произвольных постоянных С1, С2,. Сn..
б)
при любых допустимых начальных условиях
(43) найдутся такие значения С10,
С20,.
Сn0
постоянных
С1,
С2,.
Сn,
что функция
![]() будет удовлетворять этим начальным
условиям.
будет удовлетворять этим начальным
условиям.
Общее
решение дифференциального уравнения
(50) (или (49)), найденное неявно в виде:
![]() (х, у, С1,
С2,
, Сn)
= 0 называется общим
интегралом
этого уравнения.
(х, у, С1,
С2,
, Сn)
= 0 называется общим
интегралом
этого уравнения.
Всякое
решение
![]() ,
получаемое из общего решения (44) при
конкретном вполне определенном наборе
значений
,
получаемое из общего решения (44) при
конкретном вполне определенном наборе
значений
![]() постоянных
постоянных
![]() ,
называется частным
решением.
,
называется частным
решением.
Интегрирование дифференциальных уравнений n – го порядка точным аналитическим методом (в квадратурах) удается произвести только в некоторых частных случаях, которые и рассматриваются в следующих параграфах.
