- •Министерство образования и науки Российской Федерации
- •Лабораторная работа по теме «Матричные операции в Excel»
- •Матричные операции в Excel
- •Задания для самостоятельной работы
- •Лабораторная работа по теме: « Методы решения систем линейных алгебраических уравнений (слау)»
- •Метод Крамера
- •Матричный способ решения слау
- •1) Решение слау по формулам Крамера (рис.1).
- •2) Решение слау с матричным методом. (рис.2).
- •Литература
Задания для самостоятельной работы
Выполнить действия над матрицами:
3AB+(A-B)(A+2BT), где
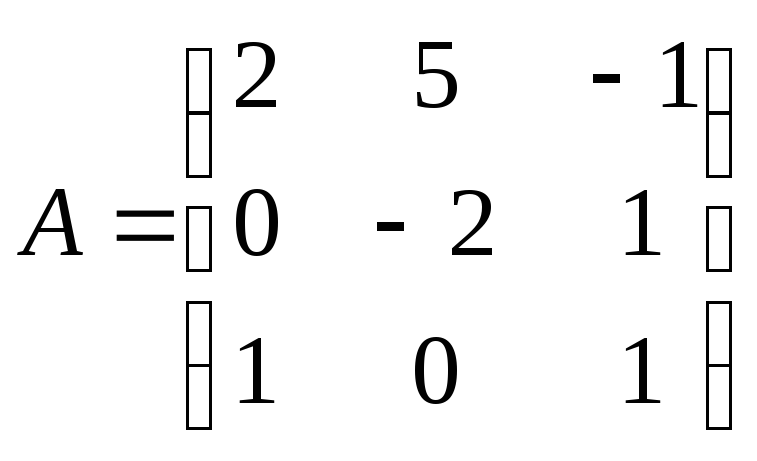 ,
,
 .
.3B(A+B)-|A|(A-1+2BT), где
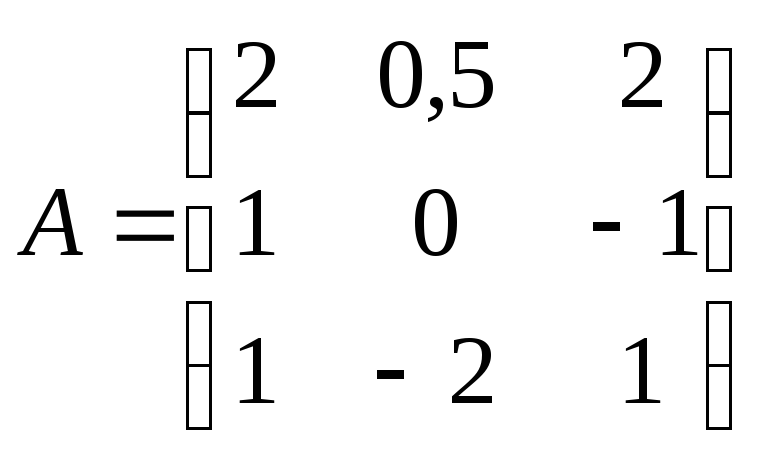 ,
,
 .
.3BT(A-B)+|B|(4AT+B-1), где
 ,
,
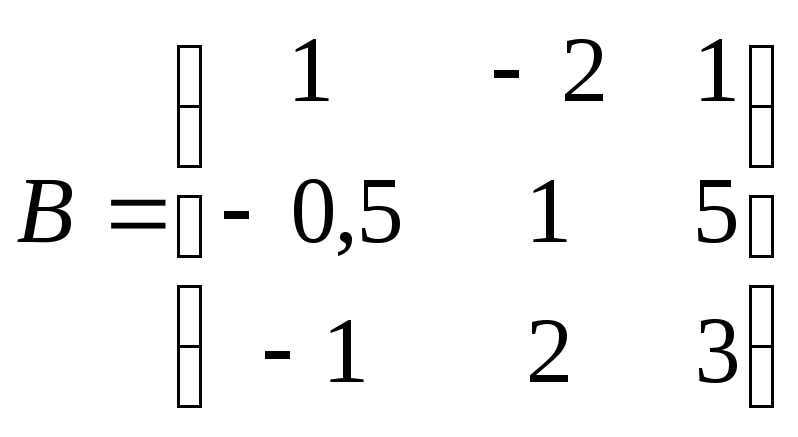 .
.
Прим.: |A| – опеделитель матрицы A. |В| – опеделитель матрицы В.
Лабораторная работа по теме: « Методы решения систем линейных алгебраических уравнений (слау)»
Цель работы: изучить методы решения СЛАУ (формулы Крамера и матричный метод) и их реализация в MS Excel.
Метод Крамера
Метод Крамера является одним из способов решения систем линейных алгебраических уравнений. Создан Габриэлем Крамером в 1750 году.
Пусть
дана система ![]() линейных алгебраических уравнений с
линейных алгебраических уравнений с ![]() неизвестными:
неизвестными:  (1)
(1)
Если определитель системы
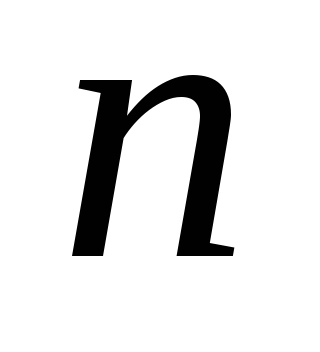 -го
порядка
-го
порядка
 не
равен нулю, то система (1) имеет единственное
решение:
не
равен нулю, то система (1) имеет единственное
решение: ![]() где
где ![]() –определитель
полученный из
–определитель
полученный из ![]() заменой
заменой ![]() -ого
столбца на столбец свободных членов
системы (1) (см.[1], стр.18, теорема 4).
-ого
столбца на столбец свободных членов
системы (1) (см.[1], стр.18, теорема 4).
Например:
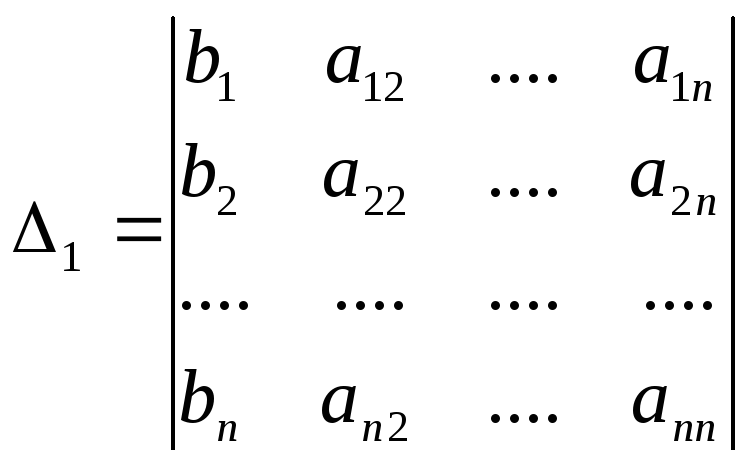 .
.
Таким
образом, суть решения СЛАУ методом
Крамера сводится к вычислению ![]() определителя и нахождению решения
системы по формулам Крамера.
определителя и нахождению решения
системы по формулам Крамера.
Матричный способ решения слау
Пусть
дана система
![]() уравнений с
уравнений с![]() неизвестными:
неизвестными:
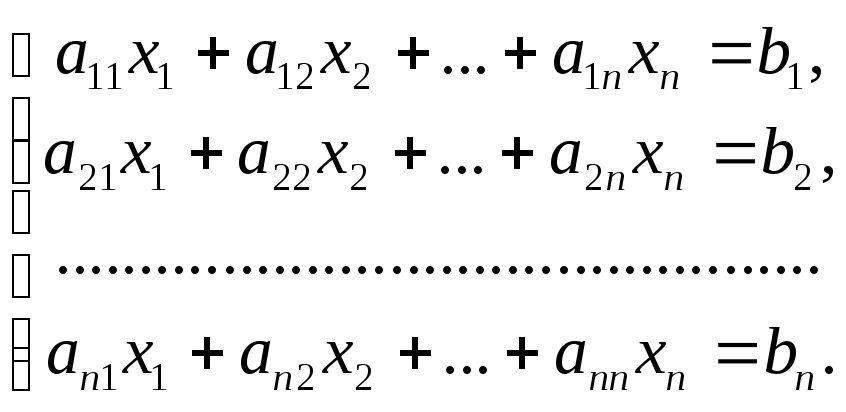 (1)
(1)
Используя
понятие произведения матриц, можно
переписать систему (1) в виде: ![]() ,
где A=
,
где A= – матрица, состоящая из коэффициентов
при неизвестных системы (1), которая
называется матрицей системы;
– матрица, состоящая из коэффициентов
при неизвестных системы (1), которая
называется матрицей системы;
х
= ![]() –
вектор-столбец, составленный из
неизвестных системы;
–
вектор-столбец, составленный из
неизвестных системы;
b
= ![]() –
вектор-столбец, составленный из свободных
членов системы.
–
вектор-столбец, составленный из свободных
членов системы.
Если
матрица А
системы линейных уравнений невырожденная,
т.е. ее определитель отличен от нуля, то
матрица А
имеет обратную. Тогда решение системы
линейных алгебраических уравнений
сводится к нахождению обратной к матрице
A,
и умножением полученной A-1
на матрицу b,
т.е. ![]() .
.
|
Задание 1. |
Решить систему линейных алгебраических уравнений двумя способами: 1) по формулам Крамера. 2) матричным способом.
|
Образец выполнения.
1) Решение слау по формулам Крамера (рис.1).
1 шаг. В ячейку А1 ввести надпись «Матрица А», в ячейку D1 ввести надпись «вектор b», в ячейку F1 внести надпись «Определитель:». Предварительно набрать в MS Word c помощью редактора Microsoft Equation данную СЛАУ. В ячейку H1 из редактора MS Word скопировать СЛАУ.
В
ячейки А2:D5
вносим матрицу коэффициентов системы
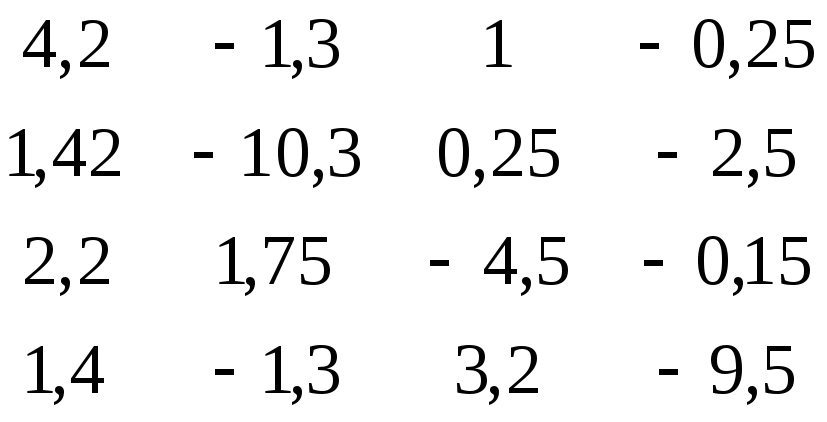 ;
в ячейкиE2:E5
вносим вектор правых частей системы:
;
в ячейкиE2:E5
вносим вектор правых частей системы:
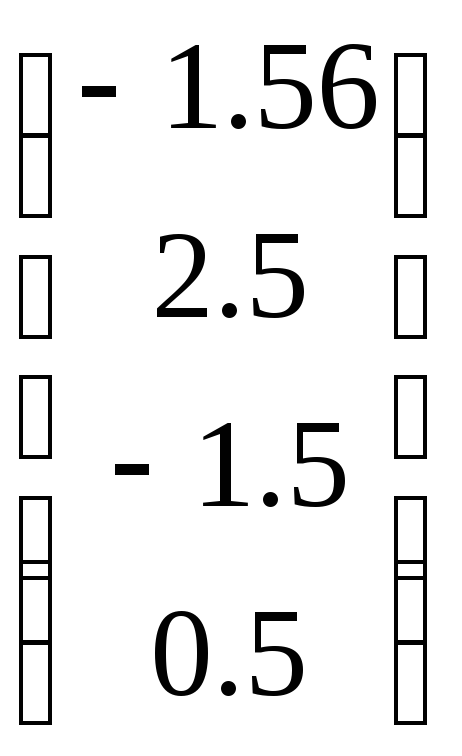 .
.
2 шаг. В ячейке G2 найдем определитель основной матрицы, для этого в основном меню выбрать: ВставкаФункцияМатематические МОПРЕД В появившемся диалоговом окне ввести диапазон A2:D5 (для этого выделить диапазон A2:D5 с помощью мышки), нажать Enter. В ячейке G2 появится посчитанный определитель матрицы -1996,46.
3
шаг. Для
подсчета ![]() ячейках А7:D10
запишем в матрице А,
заменим первый столбец столбцом сводных
членов. Для этого:
ячейках А7:D10
запишем в матрице А,
заменим первый столбец столбцом сводных
членов. Для этого:
Внесем ячейку А7:=Е2, В7:=В2, С7:=С2, D7:=D2;
Выделим диапазон А7:D7 и откопируем значения до 10-й строки.
В ячейке F7 найдем определитель полученной матрицы: ВставкаФункцияМатематическиеМОПРЕД В появившемся диалоговом окне при помощи мышки ввести диапазон A7:D10 Enter, в ячейке F7 появится посчитанный определитель матрицы 927,3689.
4
шаг. Для
подсчета ![]() в ячейках А12:D15
запишем матрицу, полученную из матрицы
А,
заменой второго столбца столбцом
свободных членов. Для этого:
в ячейках А12:D15
запишем матрицу, полученную из матрицы
А,
заменой второго столбца столбцом
свободных членов. Для этого:
Внесем ячейку А12:=А2, В12:=Е2, С12:=С2, D12:=D2;
Выделим диапазон А12:D12 и откопируем значения до 15-й строки.
В ячейке F12 найдем определитель полученной матрицы: ВставкаФункцияМатематическиеМОПРЕД В появившемся диалоговом окне при помощи мышки ввести диапазон A12:D15 Enter, в ячейке F12 появится посчитанный определитель матрицы 572,4787.
5
шаг. Для
подсчета ![]() в ячейках А17:D20
запишем матрицу чисел из диапазона
A2:D5,
полученную из матрицы А,
заменой третьего столбца вектором
свободных членов. Для этого:
в ячейках А17:D20
запишем матрицу чисел из диапазона
A2:D5,
полученную из матрицы А,
заменой третьего столбца вектором
свободных членов. Для этого:
Внесем ячейку А17:=А2, В17:=В2, С17:=Е2, D17:=D2;
Выделим диапазон А17:D17 и откопируем значения до 20-й строки.
В ячейке G17 найдем определитель полученной матрицы: ВставкаФункцияМатематическиеМОПРЕД. В появившемся диалоговом окне при помощи мышки ввести диапазон A17:D20 Enter, в ячейке G17 появится посчитанный определитель матрицы 5,0217.
6
шаг. Для
подсчета ![]() ячейках А22:D25
запишем матрицу чисел из диапазона
A2:D5,
полученную из матрицы А,
заменой четвертого столбца вектором
правых частей системы. Для этого:
ячейках А22:D25
запишем матрицу чисел из диапазона
A2:D5,
полученную из матрицы А,
заменой четвертого столбца вектором
правых частей системы. Для этого:

Внесем ячейку А22:=А2, В22:=В2, С22:=С2, D22:=Е2;
Выделим диапазон А22:D22 и откопируем значения до 25-й строки.
В ячейке G22 найдем определитель полученной матрицы: ВставкаФункцияМатематическиеМОПРЕД В появившемся диалоговом окне при помощи мышки ввести диапазон A22:D25 Enter, в ячейке G22 появится посчитанный определитель матрицы 165,094.
7 шаг. Найдем корни и сделаем проверку.
В ячейку А27 внести надпись «Проверка», в ячейку А28 внести надпись «Матрица А», в ячейку E28 внести надпись «вектор х», в ячейку F28 внести надпись «вектор b».
Внесем ячейку А29:=А2, В29:=В2, С29:=С2, D29:=D2; выделим диапазон А29:D29 и откопируем до 32 строчки.
Внесем
ячейку E29:=G6/$G$2,
E30:=G10/$G$2,
E31:=G14/$G$2,
E32:=G22/$G$2.
Получим искомый вектор 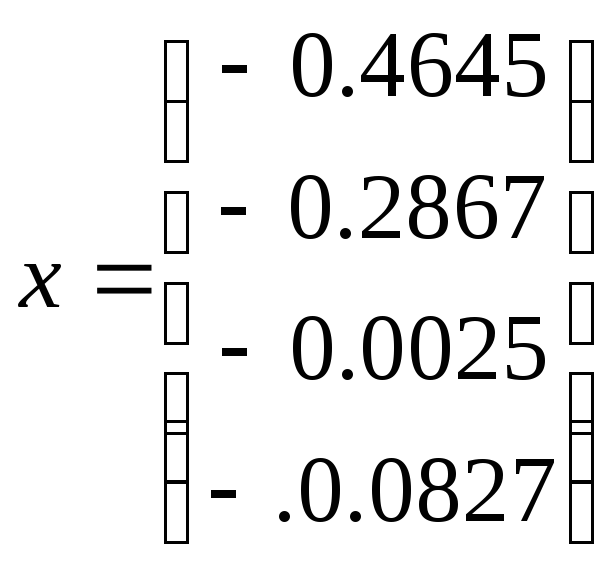 .
.
Выделим
диапазон F29:F32.
Внесем ячейку
F29:=
МУМНОЖ(А29:D32;E29:E32)
Ctrl+Shift+Enter.
Появится вектор 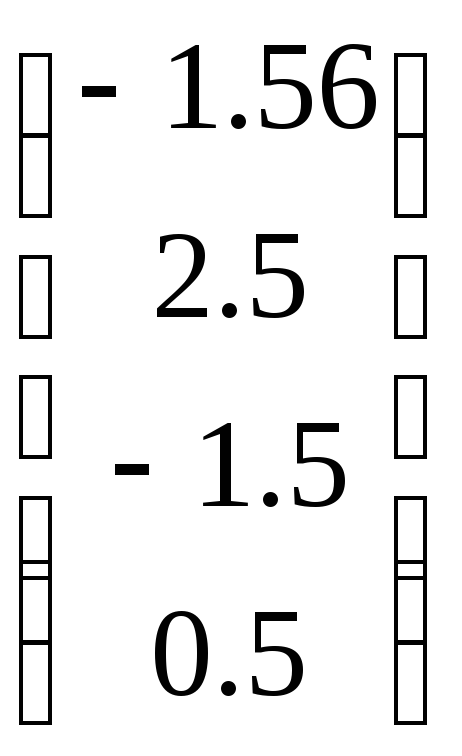 ,
равный вектору b.
,
равный вектору b.
Ответ:
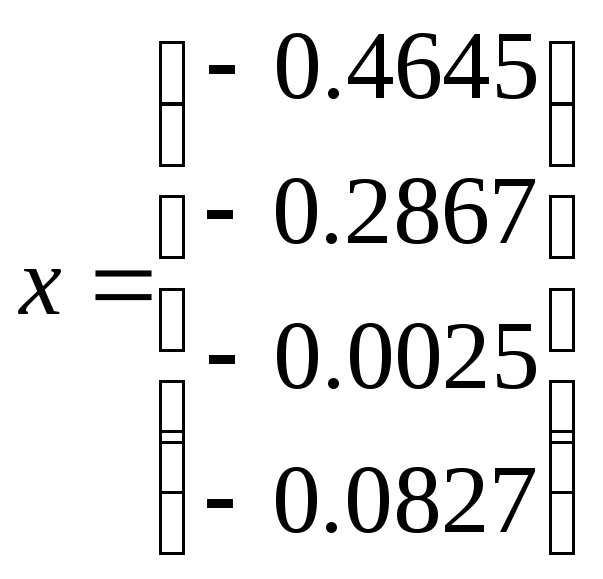 .
.