
Shpory_1
.doc
|
20 Линейные системы. Общие свойства линейных систем.
Рассмотрим
системы вида
Будем
использовать обозначения:
Дополним
систему условием:
Общие свойства линейных систем:
Пусть
система
|
21. Определитель Вронского для системы векторных функций. Теорема.ФСР
Пусть рассматривается
система векторных функций
Система линейно
независимых решений системы
Функции ФСР получаются при решении задачи Коши.
Пусть
Чтобы получить общее решение системы достаточно построить ФСР этой системы. В общем случае переменных коэффициентов общего метода построения ФСР в элементарных функциях нет. В случае постоянных коэффициентов ФСР системы можно получить всегда.
22. Решение однородных линейных систем с постоянными коэффициентами
Рассмотрим
систему уравнений
|
Можно
предложить ещё один способ решения
систем уравнений с постоянными
коэффициентами. Он позволяет решать
и неоднородные системы
23. Теорема о общем решении неоднородной линейной системы.
24 Решения неоднородных линейных систем. Метод вариации постоянных. Матрица Коши.
Рассмотрим
неоднородную систему
Пусть
Общее
решение неоднородной системы
Решить
неоднородную систему
Пусть
уже построена ФСР соответствующей
однородной системы. Тогда её общее
решение имеет вид
|
|
25 Понятие устойчивости по Ляпунову. Асимптотическая устойчивость. Точки покоя.
Рассмотрим
систему дифференциальных уравнений
Решение
Решение
Решение
Решение
Обычно
исследование на устойчивость
произвольного решения
Исследуем
на устойчивость
Все
предыдущие определения легко переносятся
в фазовые пространства. В этом случае
можно говорить об устойчивых точках
покоя, асимптотически устойчивых
точках покоя, неустойчивых точках
покоя. Если надо исследовать при
|
26.Простейшие типы точек покоя на плоскости
Будем
рассматривать систему
27. Случай комплексных корней хар. ур-ия
28 Простейшие типы точек покоя на плоскости. (Случай кратных корней)
Эта
картина получается из первого случая
Отметим,
что из условия
Проведённый анализ позволяет утверждать следующее:
Во втором случае второе собственное значение может быть нулевым. В остальных случаях требуется дополнительное условие. Приведённые утверждения остаются справедливыми, если порядок системы равен n.
|
29Исследование на устойчивость по первому приближению
Рассмотрим
произвольную нелинейную систему
Система первого приближения называется стационарной, если матрица A постоянна.
Точка
покоя
Будем
говорить, что система
В
случае, когда система
Пусть
Эти теоремы не охватывают все возможные случаи. Так, они не работают, если у матрицы A все собственные значения с неположительной вещественной частью и есть собственное значение с нулевой вещественной частью. Такой случай называется критическим. В критическом случае исследование на устойчивость по первому приближению невозможно.
На
неустойчивость либо неустойчивость
точки покоя
|

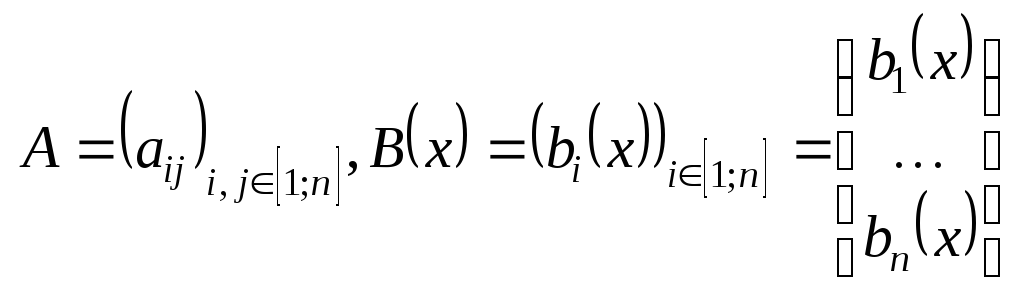 .
Будем полагать, что
.
Будем полагать, что

 .
Заметим, что
.
Заметим, что
 .
Интегрируя, получаем:
.
Интегрируя, получаем:
 ,
где
,
где
 ,
где
,
где
 – общее решение соответствующей
однородной системы, а
– общее решение соответствующей
однородной системы, а
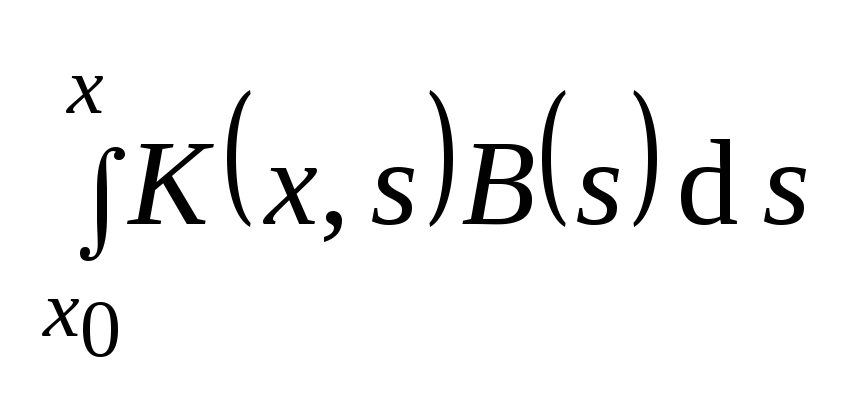 – частное решение неоднородной
системы.
– частное решение неоднородной
системы. в векторной форме:
в векторной форме:

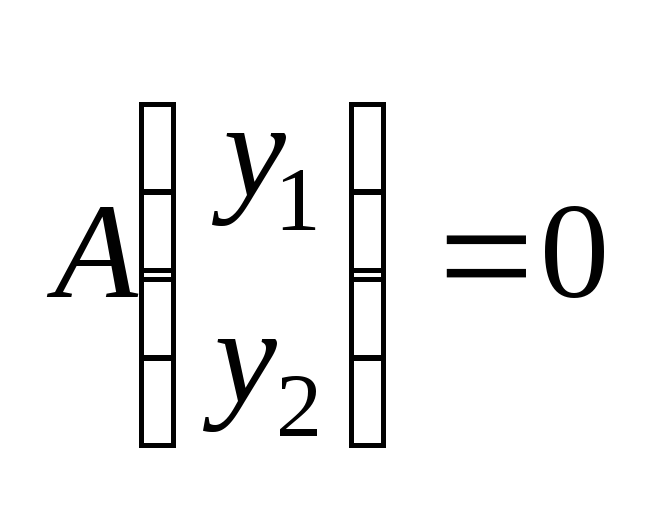 .
Если
.
Если
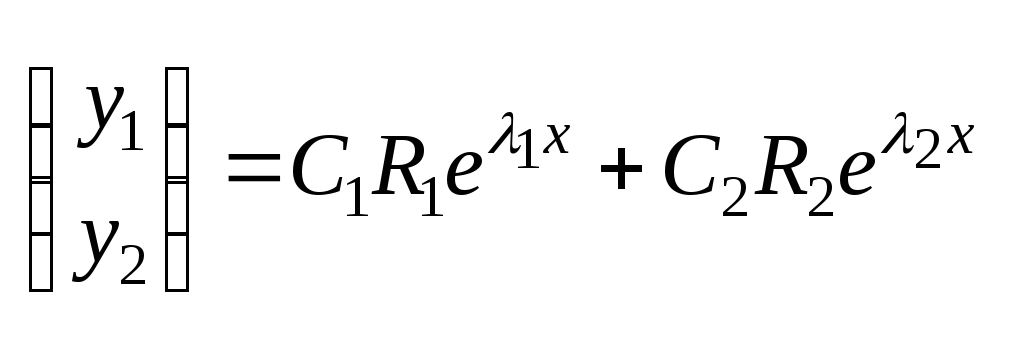 .
.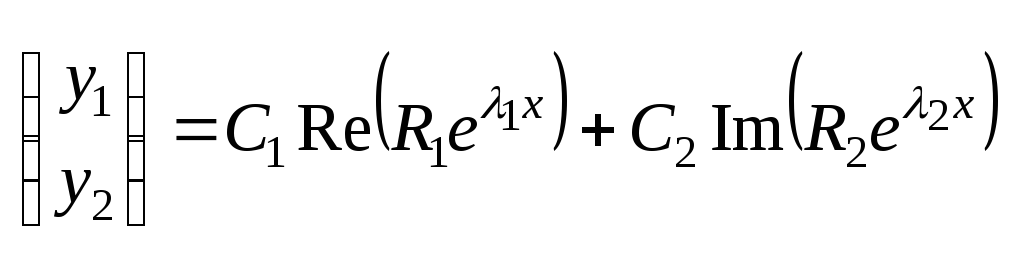 .
Удобнее записать его несколько иначе:
.
Удобнее записать его несколько иначе:
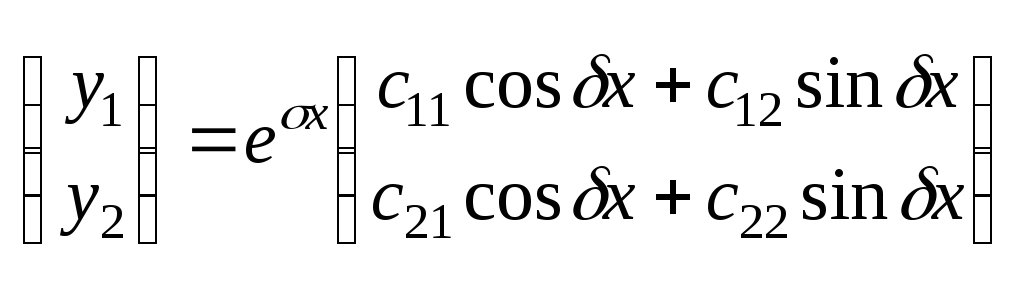 (здесь
(здесь
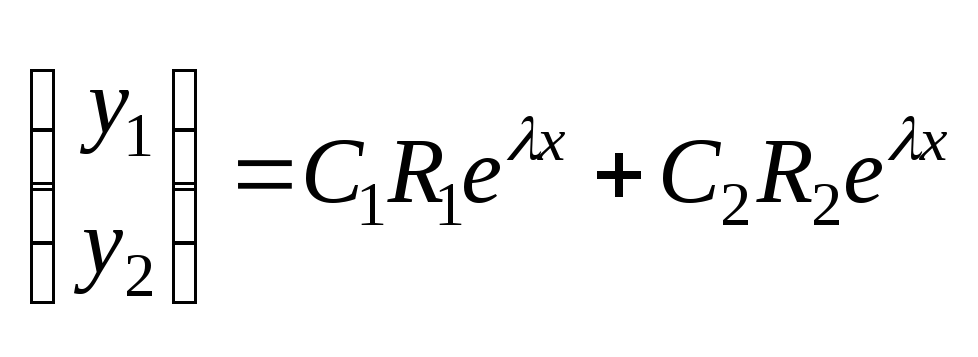 .
Все фазовые траектории прямолинейны.
При
.
Все фазовые траектории прямолинейны.
При
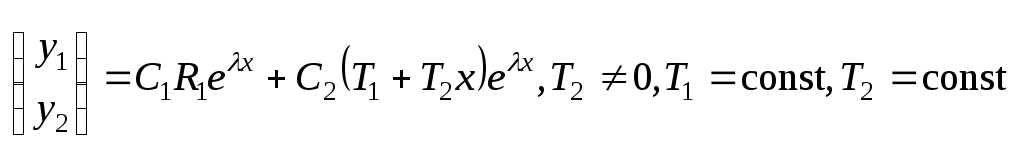 .
Модно считать, что
.
Модно считать, что