1

1.Гидравлическое сопротивление аппаратов и трубопроводов

При движении жидкости в аппаратах и трубопроводах возникают потери энергии, связанные с вязкостью жидкости (ламинарный режим) и с вихреобразованиями, перемешиванием определенных её объемов (турбулентный режим), а также потери энергии, обусловленные резким изменением конфигурации потока (резкое изменение живого сечения потока и направления потока). Потери первого типа связывают с длиной участка аппарата или трубопровода и называют их гидравлическими потерями по длине и обозначают как , второго типа – местными потерями и обозначают как . Для удобства (упрощения) расчетов считают их независимыми друг от друга и для определения общей потери напора их арифметически суммируют:

. (2.27)

Далее рассмотрим вопросы, связанные с определением и .

Ламинарное движение жидкости в трубах

Пусть жидкость входит в круглую трубу из резервуара большого размера (рис.). Во входном поперечном сечении скорости во всех точках будут одинаковы и равны . По мере удаления от входа, вследствие трения у стенок, слои жидкости, прилежащие к стенкам, начинают затормаживаться; толщина этого слоя  постепенно увеличивается, а движение, наоборот, замедляется. Центральная часть потока (ядро течения), ещё не захваченная трением, продолжает двигаться как целое. Поскольку расход жидкости – величина постоянная, уменьшение скорости в пограничном слое приведет к увеличению скорости в ядре потока. Таким образом, в середине трубы, в ядре, скорость течения всё время возрастает, а у стенок, в растущем пограничном слое , уменьшается. Это происходит до тех пор, пока пограничный слой не захватит всего сечения потока, и ядро не будет сведено к нулю. При этом 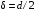. На этом формирование профиля скоростей заканчивается, в дальнейшем профиль не меняется и принимает форму, характерную для ламинарного режима течения жидкости.

. Схема развития начального участка в круглой трубе

Участок трубы, на котором происходит стабилизация профиля скоростей, называется начальным участком или участком гидродинамической стабилизации, дальнейший участок – гидродинамически стабилизированным участком. На стабилизированном участке параметры потока не меняются.

Приближенное уравнение пограничного слоя и уравнение неразрывности в цилиндрической системе координат для этого случая имеют вид:

(2.28)

Решение системы уравнений проведено многими авторами, и результаты представлены в виде:

, (2.29)

где

Для в зависимости от методов решения получены несколько разные результаты: – Буссинеск, – Тарг, – Шиллер, 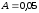– Лыков.

Необходимо отметить, что потери напора на начальном участке больше, чем на соответствующей длине стабилизированного участка. Это особенно заметно для коротких труб, длина которых меньше начального участка, т.е. .

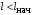Рассмотрим гидродинамически стабилизированный участок трубы (рис. 2.15).

Запишем уравнение Навье – Стокса для оси x в цилиндрических координатах r, , x:

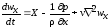. (2.30)

Рис. . Течение жидкости в круглой трубе

Заметим, что для горизонтальной трубы , течение осесимметричное, т.е. dw_x/d = 0; примем, что инерционные силы по сравнению с остальными незначительны: . Тогда из (2.30) получим:

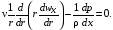(2.31)

При выводе уравнения Навье – Стокса градиенты давления по осям принимались положительными, а реально давление с ростом x уменьшается. Поэтому можно записать:

Тогда уравнение (2.31) примет вид:

(2.32)

Запишем граничные условия: при –конечная величина

Дважды проинтегрировав уравнение (2.32), получим:

(2.33)

Так как всюду должна иметь конечное значение, а при выражение (2.33) дает , то физически реальный результат получим лишь при . Для определения воспользуемся граничным условием:

Тогда получим:

(2.34)

Таким образом, распределение скоростей по сечению круглой трубы будет параболическим. Максимальное значение скорости получим при , т.е. на оси трубы:

(2.35)

Определим среднее значение скорости . Как известно:

(2.36)

Найдем . Через элементарное кольцо шириной будет проходить количество жидкости, равное (рис. 2.16):

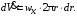(2.37)

Рис. 2.16. Расход через элементарную площадку

Полный расход через живое сечение трубы будет равен:

(2.38)

Интегрирование (2.38) с учетом (2.34) даст:

(2.39)

Найдем среднее значение скорости , подставляя в (2.36) выражение для расхода :

(2.40)

Сравнивая (2.35) и (2.40), находим, что 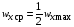. Из (2.40) определим перепад (потери) давления :

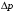(2.41)

Формула (2.41) носит название «формула Пуазейля». Этот закон Пуазейлем был установлен экспериментально.

2.Турбулентное течение жидкости в трубах

Мгновенное значение скорости можно выразить:

– осредненная по времени скорость по направлению x, – пульсационная скорость по этому же направлению

Рассмотрим поведение турбулентного потока жидкости около твердой стенки (рис. 2.17).

Рис. 2.17. Распределение скорости около твердой стенки

В ядре потока за счет пульсационных скоростей происходит непрерывное перемешивание жидкости. У твердых стенок поперечные движения частиц жидкости невозможны.

Около твердой стенки жидкость течет в ламинарном режиме. Между ламинарным пограничным слоем и ядром потока существует переходная зона.

Движение жидкости при турбулентном режиме всегда сопровождается значительно большей затратой энергии, чем при ламинарном. При ламинарном режиме энергия расходуется на вязкое трение между слоями жидкости; при турбулентном же режиме, помимо этого, значительная часть энергии затрачивается на процесс перемешивания, вызывающий в жидкости дополнительные касательные напряжения.

Для определения напряжения сил трения в турбулентном потоке используется формула:

(2.43)

где – напряжение вязкого течения, – турбулентное напряжение, вызванное перемешиванием. Как известно, 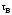определяется законом вязкого трения Ньютона:

(2.44)

_в

Следуя полуэмпирической теории турбулентности Прандтля, принимая, что величина поперечных пульсаций скорости имеет в среднем один и тот же порядок, что и продольные пульсации, можно записать:

. (2.45)

Здесь  – плотность жидкости, l – длина пути перемешивания, – градиент осредненной скорости.

Величина l, характеризующая средний путь пробега частиц жидкости в поперечном направлении, обусловлена турбулентными пульсациями. По гипотезе Прандтля, длина пути перемешивания l пропорциональна расстоянию частицы от стенки:

(2.46)

где  – универсальная постоянная Прандтля.

В турбулентном потоке в трубе толщина гидродинамического пограничного слоя растет значительно быстрее, чем для ламинарного. Это приводит к уменьшению длины начального участка. В инженерной практике обычно принимают:

(2.47)

Поэтому довольно часто влиянием начального участка на гидродинамические характеристики потока пренебрегают.

Далее рассмотрим стабилизированный участок горизонтальной круглой трубы.

Рассмотрим распределение осредненной скорости по сечению трубы. Примем касательное напряжение в турбулентном потоке постоянным и равным напряжению в стенке . Тогда после интегрирования уравнения (2.44) получим:

. (2.48)

Здесь – величина, имеющая размерность скорости, поэтому называется динамической скоростью.

Выражение (2.48) представляет собой логарифмический закон распределения осредненных скоростей для ядра турбулентного потока.

Путем несложных преобразований формулу (2.48) можно привести к следующему безразмерному виду:

(2.49)

где – безразмерное расстояние от стенки; M – константа.

Как показывают опыты,  имеет одинаковое значение для всех случаев турбулентного течения . Значение M было определено опытами Никурадзе: 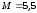. Итак, имеем:

(2.50)

В качестве безразмерного параметра, характеризующего толщину соответствующих зон, используется комплекс :

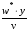вязкий ламинарный подслой: ,

переходная зона: ,

турбулентное ядро: .

При турбулентом режиме отношение осредненной скорости к максимальной осевой составляет от 0,75 до 0,9.

Зная закон распределения скоростей (рис. 2.18), можно найти величину гидравлических сопротивлений. Однако для определения гидравлических сопротивлений можно использовать более простое соотношение, а именно: критериальное уравнение движения вязкой жидкости, полученное ранее, в первой части дисциплины.

Рис. 2.18. Распределение скоростей в трубе

при ламинарном и турбулентном режимах

Для горизонтальной прямой трубы в случае напорного течения вязкой жидкости критериальное уравнение имеет вид:

(2.51)

где – геометрические комплексы, – критерий Рейнольдса, – критерий Эйлера. Они определяются как:

где ∆ – абсолютная шероховатость трубы, l – длина трубопровода, d – внутренний диаметр трубы. Из опыта известно, что потери давления прямо пропорциональны . Поэтому можно записать:

(2.52)

Далее обозначим неизвестную функцию 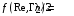, распишем критерий Эйлера . Тогда из уравнения (2.52) для потери давления получим:

(2.53)

где  – коэффициент гидравлического трения, w – средняя скорость потока.

Полученное уравнение носит название уравнение Дарси – Вейсбаха. Уравнение (2.53) может быть представлено в виде потери напора:

(2.54)

Таким образом, расчет потери давления 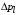или напора сводится к определению коэффициента гидравлического трения .

3. График Никурадзе

Среди многочисленных работ по исследованию зависимости выберем работу Никурадзе. Никурадзе подробно исследовал эту зависимость для труб с равномерно-зернистой поверхностью, созданной искусственно (рис. 2.19).

.

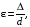
Рис. 2.19. График Никурадзе

Значение коэффициента определяется по эмпирическим формулам, полученным для различных областей сопротивления по кривым Никурадзе.

1. Для ламинарного режима течения, т.е. при , коэффициент  для всех труб независимо от их шероховатости определяется из точного решения задачи о ламинарном течении жидкости в прямой круглой трубе по формуле Пуазейля:

(2.55)

2. В узкой области наблюдается скачкообразный рост коэффициента сопротивления. Эта область перехода от ламинарного режима к турбулентному характеризуется неустойчивым характером течения. Здесь наиболее вероятен на практике турбулентный режим и правильнее всего пользоваться формулами для зоны 3. Можно также применить эмпирическую формулу:

(2.56)

3. В области гидравлически гладких труб при толщина ламинарного слоя у стенки  больше абсолютной шероховатости стенок , влияние выступов шероховатости, омываемых безотрывным потоком, практически не сказывается, и коэффициент сопротивления вычисляется здесь на основе обобщения опытных данных по эмпирическим соотношениям, например по формуле Блаузиуса:

(2.57)

4. В диапазоне чисел Рейнольдса наблюдается переходная область от гидравлически гладких труб к шероховатым. В этой области (частично шероховатых труб), когда , т.е. выступы шероховатости с высотой, меньшей средней величины , продолжают оставаться в пределах ламинарного слоя, а выступы с высотой, большей средней, оказываются в турбулентной области потока, проявляется тормозящее действие шероховатости. Коэффициент  в этом случае подсчитывается также из эмпирических соотношений, например по формуле Альштуля:

(2.58)

5. При толщина ламинарного слоя у стенки  достигает своего минимального значения, т.е. и не меняется с дальнейшим ростом числа Re. Поэтому  не зависит от числа Re, а зависит лишь от . В этой области (шероховатых труб или области квадратичного сопротивления) для нахождения коэффициента может быть рекомендована, например, формула Шифринсона:

(2.59)

В этой зоне значение  находится в пределах .

Были проведены исследования для определения  с естественной шероховатостью. Для этих труб вторая зона не определяется. Для расчета  обычно предлагаются вышеуказанные формулы.

Способы уменьшения гидравлических сопротивлений

Использование полимерных добавок и добавок поверхностно-активных веществ (ПАВ).

Как показывают эксперименты, добавка малых доз полимера или ПАВ в турбулентный поток жидкости существенно (до 60–80 ) снижает гидродинамическое сопротивление. Действие добавок при снижении проявляется в увеличении толщины ламинарного подслоя и промежуточной зоны. Макромолекулы, попадая в область больших градиентов скорости, которые имеют место в пристенной области, выпрямляются по направлению течения и создают анизотропию вязкости, увеличивая поперечную составляющую по сравнению с продольной: Увеличение вязкости в непосредственной близости от стенки приводит к утолщению ламинарного подслоя. Как следствие, снижаются в несколько раз пристеночные поперечные пульсации скоростей и давлений. Наибольший эффект снижения дают полимеры с линейно вытянутыми молекулами, без больших боковых цепей, большими молекулярными массами и хорошо растворимыми в перекачиваемой жидкости. Как показывают эксперименты, для каждого полимера имеется оптимальный диапазон изменения его концентраций; для каждой концентрации полимера имеется своё пороговое число (рис. 2.20).

Рис. 2.20. График изменения коэффициента сопротивления 

для водных растворов полиакриламида

Другие способы снижения . Влияние на поток может быть достигнуто отсосом или сдувом пограничного слоя, колебанием обтекаемой поверхности. Амплитуда таких колебаний не должна превышать толщину ламинарного подслоя.

Эффект уменьшения может быть достигнут нагревом стенок трубы с целью уменьшения молекулярной вязкости около стенки.

Необходимо отметить, что все способы уменьшения реализуются только при турбулентном режиме течения жидкости по трубопроводу.

4. Местные гидравлические сопротивления.

Местные гидравлические потери возникают при резкой деформации живого сечения потока и его направления. В зоне местных сопротивлений (рис. 2.21) происходит обтекание местных препятствий с образованием водоворотных зон и интенсивным обменом частицами жидкости основного потока и этих зон; транзитный поток отрывается от стенок, и возникают вихреобразования.

Рис. Примеры местных сопротивлений:

1 – расширение; 2 – сужение; 3 – диафрагма; 4 – вход в трубу;

5 – вход в резервуар; 6 – задвижка; 7–8 – повороты; 9 – тройник

Расчетную формулу для местного сопротивления, как формулу Дарси – Вейсбаха, получим из критериального уравнения движения вязкой жидкости:

Как известно, критерий Эйлера определяется как:

Обозначим неизвестную функции как:

В результате для расчета потери давления на местном сопротивлении получим:

(2.60)

Для потери напора можно записать:

где  – коэффициент местного сопротивления. Коэффициент  показывает, какая часть динамического давления 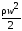теряется на данном местном сопротивлении или, если , сколько теряется на данном местном сопротивлении.

Рассмотрим  более подробно. В общем случае можно записать:

(2.61)

где – потеря напора, обусловленная вязкостным трением на данном местном сопротивлении, – потери, связанные с отрывом и вихреобразованием. С учетом уравнений Дарси – Вейсбаха и (2.60) можно записать:

или (2.62)

Как показывают экспериментальные исследования, для турбулентного режима первый член правого уравнения вырождается. Поэтому для турбулентного потока принимают . Поскольку в технологических установках в большинстве случаев реализуется турбулентный режим, поэтому в справочниках приводится именно .

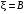Значение  обычно определяют экспериментально, и его значение зависит от конфигурации местного сопротивления. Для одного случая, для внезапного расширения потока, значение  может быть определено теоретическим путем:

(2.63)

где и – соответственно, площадь потока до и после расширения, – скорость потока до расширения. Формула (2.63) называется формулой Бордо.

6. Классификация трубопроводов.

Простым называется трубопровод, состоящий из одной линии труб, с одним расходом, хотя и из разного диаметра. Все остальные трубопроводы называются сложными. На рис представлены (из множества возможных) наиболее распространенные схемы сложных трубопроводов. Однако эти схемы необходимо рассматривать как элементы ещё более сложных схем. Например, обеспечение водой жилого дома выглядит так: разветвленная сеть в подвале дома (в каждый подъезд), разветвленная сеть в подъезд (в каждую квартиру) и разветвление в самой квартире.

Трубопроводные схемы жилых районов города и промышленных предприятий выглядят достаточно сложно.

Расчет простых трубопроводов

На рис. 2.23 представлена схема простого трубопровода постоянного диаметра. На схеме определим два характерных сечения и для них напишем уравнение Бернулли. В нашем случае таковыми являются сечения 0–0 и 1–1:

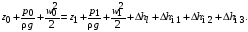(2.65)

Рис. 2.23. Схема простого трубопровода

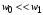Рассмотрим члены уравнения (2.65). Обозначим давления , – скорость опускания уровня жидкости в резервуаре и – скорость движения жидкости в трубопроводе. Тогда можно записать:

(2.66)

Уравнение (2.66) можно представить в виде:

(2.67)

где Следовательно, напор Н идет на создание кинетической энергии потока (первый член правой части уравнения (2.67)) жидкости и на преодоление гидравлических сопротивлений потока.

7. Определение оптимального диаметра трубопровода

При проектировании трубопроводных систем часто возникают проблемы определения оптимального диаметра трубопровода . Предположим, что известны Расчетные формулы:

(2.100)

Для ламинарного режима:

Для турбулентного режима:

Потребный напор системы:

(2.101)

Мощность потока:

Мощность насоса:

(2.102)

где 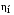– КПД насоса, – КПД электродвигателя.

Оптимальный (наиболее экономически выгодный) диаметр определяется на основе технико-экономических расчетов.

Уменьшение диаметра трубопровода приводит к увеличению мощности насоса N_н; увеличение d – наоборот к уменьшению N_н. Но увеличение диаметра приведет к увеличению стоимости трубопровода и строительства трубопроводной сети. Итак, необходимо учитывать как затраты эксплуатационные, так и капитальные. Эксплуатационные затраты : расход электроэнергии на работу насоса, обслуживание трубопроводной сети, ремонт сети и управленческие расходы. Капитальные затраты : стоимость насоса и трубопроводов, стоимость сооружений и амортизационные расходы. Полная стоимость варианта трубопроводной сети:

, (2.103)

где t – срок окупаемости сооружения. Обычно лет.

Таким образом, задача определения оптимального диаметра трубопровода сводится к определению минимума полной стоимости трубопроводной сети С. Задача может быть решена разными методами:

– математический (определение минимума функции С);

– графический;

– подбор вариантов.

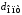Математический метод – это задача однопараметрической оптимизации. Определяем первую производную С по и приравниваем её к нулю; оттуда находим . При этом вторая производная должна быть больше нуля.