
Illyustratsii_k_lektsiam_TsOS
.pdf
Дисциплина:
Цифровая обработка сигналов – ЦОС
(иллюстрационный материал для лекций)
Сигналы и их спектральное представление
Основные типы сигналов
Сигнал |
Рис. |
Область определения |
Область значений |
Аналоговый |
а |
непрерывная |
непрерывная |
Дискретный |
б |
дискретная |
непрерывная |
Квантованный |
в |
непрерывная |
дискретная |
Цифровой |
г |
дискретная |
дискретная |
а) |
б) |
в) |
г) |
1
Задержанный единичный импульс |
|
|
|
|
|
|
|
|
δ(n −2) |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1, n = k |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ(nT −kT ) = δ(n −k) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, n ≠ k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
0 |
1 |
2 |
3 |
|
n |
||||||||||||||
|
|
|||||||||||||||||||
|
x(n) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Единичный ступенчатый сигнал |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В дискретной форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
0 |
1 |
2 |
3 |
|
n |
||||||||||||||
|
|
|||||||||||||||||||
1, n ≥ 0, n = 0, 1, 2, ... |
∞ |
|
x(n) = |
x(n) = ∑ δ(n −k) |
|
0, n < 0 |
k = |
0 |
Математическая запись любого дискретного сигнала имеет вид:
∞
x(n) = ∑x(k)·δ(n −k)
k =0
Итак, согласно выражению (1) дискретный сигнал представляет сумму δ - функций, следующих с интервалом времени Т. Эти функции имеют амплитудные коэффициенты, равные отсчетам сигнала x(t) в точках дискретизации kT.
Обобщенная схема цифровой обработки аналоговых сигналов
Задачи ЦОС сигнала обычно сводятся к трем действиям:
–ввод цифрового сигнала, или преобразование входного аналогового сигнала в цифровую форму;
–обработка полученного массива данных с использованием различных алгоритмов;
–вывод полученного результата, или обратное преобразование цифрового сигнала в аналоговую форму.
Примеры некоторых дискретных сигналов
Единичный импульс ( δ -импульс) - δ -функция в дискретной форме:
1, n = 0 |
1 |
|
δ(n) |
||||||||||||
|
|||||||||||||||
δ(nT ) = |
|
|
|
|
|
|
|
|
|
||||||
0, n ≠ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
- |
|
2 |
-1 0 1 2 3 |
||||||||||||
Обобщенная схема ЦОС
~
x(t) ФНЧ x (t)
АЦП |
x(nT ) Устройство y(nT ) |
ЦОС |
|
|
(вычислитель) |
fд
|
~ |
Сглажи- |
y(t) |
ЦАП |
y(t) |
вающий |
|
|
|
ФНЧ |
|

Дискретизация непрерывных сигналов. Дискретные сигналы.
Обозначение дискретных сигналов x(nT), x(n), xn , {x0; x1; x2; …}.
∞
x(n) = ∑x(k)δ(n −k)
k =−∞
2
Различие спектров непрерывного и дискретного сигналов
x(t) – непрерывный сигнал |
|
|
|
|
|
|
|
|
|
||
x(n) – дискретный сигнал |
|
|
|
|
|
|
|
|
|
||
Комплексная спектральная плотность (спектр) |
X ( j f ) , |
X ( j ω) , X (e jω) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
ПФ |
Преобразование Фурье (ПФ) аналогового сигнала |
x(t) X (e jω ) |
||||||||||
Прямое преобразование Фурье |
|
|
|
|
|
|
|
|
|||
|
|
∞ |
|
|
|
|
|
|
|
|
∞ |
X ( j ω) = X (e jω) = ∫x(t) e− j ωt dt |
или |
|
X ( j |
f ) = ∫x(t) e− j 2 π f t dt |
|||||||
|
|
−∞ |
|
|
|
|
|
|
|
|
−∞ |
Обратное преобразование Фурье |
|
|
|
|
|
|
|
|
|||
x(t) = ∞∫X ( j f ) e j 2 π f t df или |
x(t) = |
1 |
|
∞∫X ( j ω) e j ωt dω |
|||||||
|
|
|
|||||||||
−∞ |
|
|
|
|
2π −∞ |
|
|
||||
Прямое и обратное преобразование Фурье для дискретных сигналов |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
ДВПФ |
Дискретное во времени преобразование Фурье (ДВПФ) |
x(n) X (e jω ) |
||||||||||
прямое ДВПФ |
|
|
|
|
|
|
|
|
|
||
|
|
∞ |
|
|
∞ |
|
|
|
|
|
|
X (e jω) = ∑x(n)e− jωn или X ( j f ) = |
∑x[n] e − j 2 π f |
n T |
|||||||||
|
n=−∞ |
|
n=−∞ |
|
|
|
|
||||
обратное ДВПФ |
|
|
|
|
|
|
|
|
|
||
|
1 |
π |
|
|
1 |
|
fд |
|
|
|
|
x(n) = |
∫X (e jω) e jωndω или |
x[n] = |
|
∫X ( j |
f ) e j 2 πf n T df |
||||||
2π |
fд |
|
|||||||||
|
−π |
|
|
0 |
|
|
|
|
|||

Спектры непрерывных и дискретных сигналов
«Реальный» сигнал – сигнал, ограниченный по времени
«Идеальный» сигнал – сигнал, ограниченный по частоте
Спектр периодического сигнала
Спектр непрерывного сигнала
Спектр дискретного сигнала
3
Прямое и обратное дискретное преобразование Фурье (ДПФ)
|
|
N −1 |
|
2π |
|
|
|
|
|
|
|
|
|
|
X (m) = ∑x(n)e− j |
|
m n , m = |
|
|
|
|
|
|||||
прямое ДПФ: |
N |
0, N −1. |
|||||||||||
|
|
n=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
N −1 |
|
|
2π |
|
|
|
|
|
|
|
x(n) = |
|
∑X (m)e j |
|
m n ,n = |
|
|
|
|||||
обратное ДПФ: |
|
N |
0, N −1. |
||||||||||
|
|
||||||||||||
|
|
N m=0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Линейные системы с постоянными параметрами (ЛПП-системы)
x(n) y(n)
ЛПП
Линейность – выполнение принципа суперпозиции
x1(n) → y1(n) |
x2 (n) → y2 (n) |
|
вход - |
Ax1(n) + Bx2 (n) , |
A , B − const |
выход - |
Ay1 (n) + By2 (n) |
|
Постоянство параметров –
независимость параметров от времени (инвариантность от времени) x(n) → y(n)
x(n −n0 ) → y(n −n0 )
Импульсная характеристика - h(n)
x(n) y(n)
ЛПП
h(n) – реакция на δ(n)
x(n) → y(n)
x(n) = δ(n) → y(n) = h(n)
Система реализуема (физически реализуема)
h(n) = 0 при n < 0
Система устойчива
Необходимое и достаточное условие устойчивости системы:
∞
∑h(n) < ∞
n=−∞
4
∞
вход - x(n) = ∑x(m) δ(n −m)
m=−∞
Дискретная СВЕРТКА
∞ |
∞ |
выход - y(n) = ∑x(m) h(n −m) |
или y(n) = ∑h(m) x(n −m) |
m=−∞ |
m=−∞ |
Уравнение дискретной свертки y(n) = ∑n h(m) x(n −m)
m=0
Пример графического построения свертки (первый вариант)
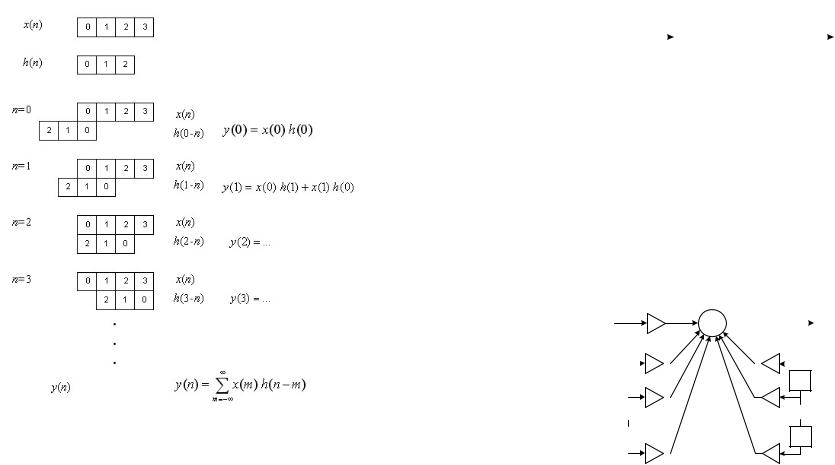
5
Пример графического построения свертки (второй вариант) |
Линейные разностные уравнения с постоянными |
||||||||||||||||||||||
коэффициентами (разностное уравнение) |
|||||||||||||||||||||||
|
|||||||||||||||||||||||
|
x (n) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y ( n ) |
|||||||
|
|
|
|
|
Л П П - система |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
h(n ) |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Линейное разностное уравнение N-го порядка, связывающее входной сигнал |
||||||||||||||||||||||
|
|
|
|
|
|
|
x(n) с выходным y(n) |
|
|
|
|
|
|
|
|||||||||
|
N |
|
|
|
|
|
M |
|
|
|
|
|
|
|
|||||||||
|
∑ak y(n −k) = ∑bk x(n −k) , n ≥ 0 |
||||||||||||||||||||||
|
k =0 |
|
|
|
|
|
k =0 |
|
|
|
|
|
|
|
|||||||||
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
M |
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
||||||
|
y(n) = ∑ bk x(n −k) −∑ ak y(n −k) , a0 =1 |
||||||||||||||||||||||
|
|
k =0 |
|
|
|
|
|
|
k =1 |
|
|
|
|
|
|
|
|||||||
|
коэффициенты ak и bk полностью характеризуют систему |
||||||||||||||||||||||
|
Как и в случае свертки, разностное уравнение не только дает теоретическое |
||||||||||||||||||||||
|
описание системы, но может быть также основой для реализации системы. |
||||||||||||||||||||||
|
x(n) |
b0 |
+ |
|
|
|
y(n) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Z-1 |
|
|
b1 |
|
|
− a1 |
|
|
|
Z-1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
b2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Z-1 |
|
|
|
− a2 |
|
|
|
Z-1 |
|
||||||||||||
|
|
|
|
|
|
... ... |
|
||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
... ... |
|
|
||||||||||||||||||||
|
|
Z-1 |
|
bM |
|
|
− aN |
|
|
|
Z-1 |
||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
Нерекурсивная часть |
Рекурсивная часть |
|||||||||||||||||||||
|
(трансверсальная) |
цифрового фильтра |
|||||||||||||||||||||
|
цифрового фильтра |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
В общем случае линейная система, может иметь импульсную характеристику
как конечной, так и бесконечной длительности.
КИХ-системы, БИХ-системы КИХ – конечная импульсная характеристика БИХ – бесконечная импульсная характеристика
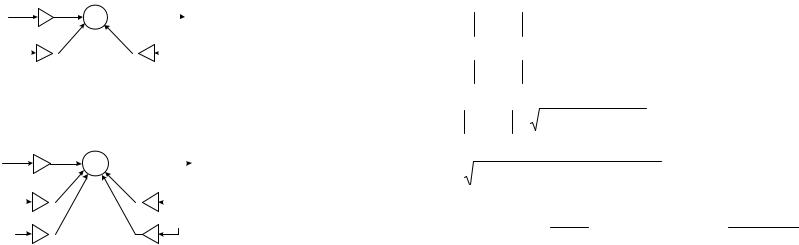
Для КИХ-системы N=0
|
|
M |
N |
разностное уравнение y(n) = ∑ bk |
x(n −k) −∑ ak y(n −k) |
||
|
|
k =0 |
k =1 |
M |
|
|
|
записывается как y(n) = ∑b(k)x(n −k) |
|||
k =0 |
|
|
|
|
|
|
M |
совпадает с уравнением свертки y(n) = ∑h(k)x(n −k) |
|||
|
|
|
k =0 |
b , |
n = 0, 1, ... , M ; |
||
и, следовательно, h(n) = |
n |
- востальныхслучаях. |
|
|
0 |
||
Отсчеты импульсной характеристики h(n) равны коэффициентам разностного |
|||
уравнения b(k) . |
|
|
|
Для БИХ-системы |
N > 0 |
(обратные связи) |
|
разностное уравнение |
|
|
|
M |
|
N |
|
y(n) = ∑ bk x(n −k) −∑ ak y(n −k) |
|||
k =0 |
|
k =1 |
|
Примеры:
разностное уравнение первого порядка
y(n) =b0 x(n) +b1x(n −1) −a1 y(n −1)
Схема реализации разностного уравнения первого порядка
x(n) |
b0 |
+ |
|
|
|
y(n) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z-1 |
|
b1 |
|
|
−a1 |
|
Z-1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
разностное уравнение второго порядка
y(n) = b0 x(n) +b1x(n −1) +b2 x(n −2) −a1 y(n −1) −a2 y(n −2)
Схема реализации разностного уравнения второго порядка
x(n) |
b0 |
+ |
|
|
|
y(n) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z-1 |
|
b1 |
|
|
−a1 |
|
Z-1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z-1 |
|
b2 |
|
|
− a2 |
|
Z-1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
6
Представление дискретных сигналов и систем в частотной области
x(n) – дискретный сигнал
X (e jω) , X ( j ω) – комплексная спектральная плотность (спектр)
ДВПФ
Дискретное во времени преобразование Фурье (ДВПФ) x(n) X (e jω)
h(n) – импульсная характеристика ЦФ
H (e jω) , H ( j ω) – частотная характеристика ЛПП-системы (ЦФ)
с импульсной характеристикой h(n)
ДВПФ
h(n) H (e jω)
Прямое ДВПФ – ряд Фурье
∞
H (e jω) = ∑h(k)e− jωk
k =−∞
В общем случае H (e jω) – комплексная функция и может быть выражена через свои действительную и мнимую части
H (e jω) = Re(H (e jω))+ j Im(H (e jω))
или через модуль и аргумент
H (e jω) = H (e jω) e− j arg H (e jω )
или |
|
|
H (e jω) = H (e jω) exp[− j arg H (e jω)] |
|
|
модуль – АЧХ – амплитудно-частотная характеристика |
|
|
H (ω) = H (e jω) = Re(*)2 +Im(*)2 |
|
|
или |
|
|
H (ω) = (Re[H ( jω)])2 +(Im[H ( jω)])2 |
|
|
аргумент – ФЧХ – фазо-частотная характеристика |
Im[H ( jω)] |
|
ϕ(ω) = arg(H (e jω))= arctg Im(*) |
или ϕ(ω) = arctg |
|
Re(*) |
|
Re[H ( jω)] |

Частотная характеристика H(ejω) является непрерывной функцией частоты.
Кроме того, это периодическая функция частоты ω с периодом 2π.
Поскольку H(ejω) – периодическая функция частоты, она может быть представлена в виде ряда Фурье:
∞
H (e jω) = ∑h(k)e− jωk ,
k=−∞
вкотором коэффициентами Фурье являются значения импульсной характеристики
h(n), т.е. h(n) могут быть определены через |
H (e jω) как коэффициенты Фурье |
||||||
периодической функции: |
|
|
|
|
|||
h(n) = |
1 |
∫π H (e jω) e jωndω – обратное ДВПФ |
|||||
2π |
|||||||
|
|
|
|
−π |
|
||
|
|
|
|
|
∞ |
|
|
|
H (e jω) = ∑h(n)e− jωn |
– прямое ДВПФ |
|||||
|
|
|
|
|
n=−∞ |
|
|
ДВПФ – дискретное во времени преобразование Фурье |
|||||||
|
∞ |
|
|
|
|
||
прямое X (e jω) = ∑x(n)e− jωn |
|
||||||
|
n=−∞ |
|
|
||||
обратное x(n) = |
1 |
|
∫π X (e jω) e jωndω |
|
|||
2π |
|
||||||
|
−π |
|
|
||||
СВОЙСТВО дискретное во времени преобразование Фурье от свертки
∞
y(n) = ∑h(k)x(n −k)
k =−∞
Y (e jω) = H (e jω) X (e jω).
7
Z-преобразование дискретного сигнала
преобразование Фурье дискретного времени – прямое ДВПФ
∞ |
∞ |
|
X (e jω) = ∑x(n)e− jωn или |
X ( j f ) = ∑x[n] e − j 2 π f n T |
|
n=−∞ |
n=−∞ |
|
произведем замену, введем комплексную переменную z |
|
|
|
e j 2 πf T = z |
e j ω = z |
Z-преобразование
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
X (z) = ∑x[n] z − n |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
n=−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
одностороннее Z-преобразование |
|
|
|
|
|
|
|
|
|
|
||||
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X (z) = ∑x[n] z − n применимо для сигналов, для которых x[n] = 0 при n < 0 |
||||||||||||||
n=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример |
1 , |
n =1, 2, 3 |
|
|
|
|
|
|
|
|||||
x[n] = |
n >3, n < 0 |
|
|
|
|
|
|
|
||||||
|
0, |
|
|
|
|
|
|
|
||||||
X (z) = z−1 + z−2 + z−3 = |
z2 + z +1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
z3 |
|
|
|
|
|
|
|
|
|
|
Пример |
x[n] = e−αnT , n > 0 |
|
|
|
|
|
|
|
|
|
|
|||
|
∞ |
|
∞ |
|
|
|
∞ |
−αT z−1 )n |
||||||
X (z) = ∑x[n] z−n = |
∑e−αnT z−n = ∑(e |
|||||||||||||
|
n=0 |
|
n=0 |
|
|
|
n=0 |
|
|
|
|
|
|
|
Из теории рядов следует, что при выполнении условия |
|
e−αT z−1 |
|
<1 сумма |
||||||||||
|
|
|||||||||||||
ряда X (z) равна X (z) = |
|
1 |
= |
|
|
z |
|
|
|
|
|
|
||
1 −e−αT z−1 |
z −e−αT |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
Z-преобразование X (z) дискретного сигнала x[n] определено только для области z, в которой степенной ряд (1) сходится.
Эта область сходимости включает в себя все значения z, находящиеся вне некоторого круга на комплексной z-плоскости, радиус которого r0 , который
называется радиусом сходимости, т.е. при r0 < z < ∞ ряд сходится.

Область сходимости степенного ряда
В области сходимости существует взаимно-однозначное соответствие между
X (z) и x[n] , |
т.е. каждому x[n] соответствует одно и только одно X (z) , |
|||
определенное для |
|
z |
|
> r0 и наоборот. |
|
|
|||
Свойства Z-преобразования
∞ |
∞ |
X (z)= ∑x[n]z−n , Y (z)= ∑y[n]z−n |
|
n=−∞ |
n=−∞ |
1. Свойство линейности
Последовательность ax[n] +by[n] имеет Z-преобразование aX (z)+bY (z)
2. Свойство задержки
Последовательность x[n −m] имеет Z-преобразование z−m X (z)
z−m – множитель задержки
Элемент задержки
на входе x[n] Z −пр X (z) x(n) z -1 x(n-1)
Z −пр
на выходе x[n −1] z−1 X (z)
z−1 – передаточная функция элемента задержки на один отсчет
3. Свойство свертки
∞
Последовательность y[n] = x[n] h[n] = ∑x[m]h[n −m] - свертка
m=−∞
имеет Z-преобразование Y (z)= X (z)H (z)
8
Обратное Z-преобразование
Обратный переход от z–преобразования X(z) к последовательности x(n) определяется соотношением
x[n] = |
1 |
∫X (z)zn−1dz , где C – замкнутый контур. |
|
2πj |
|||
|
C |
Это обратное z–преобразование содержит интеграл по любому замкнутому контуру с направлением обхода против часовой стрелки, расположенному в области сходимости и окружающему начало координат.
Способы нахождения обратного Z-преобразования
1.Прямое вычисление с помощью теоремы о вычетах.
2.Разложение X (z) на простые дроби.
3.Разложение X (z) в степенной ряд.
1. Прямое вычисление с помощью теоремы о вычетах.
Для рациональных z–преобразований контурные интегралы вида (2) удобно вычислять с помощью теоремы о вычетах, согласно которой
x(n) = ∑res X (z)zn−1 , |
||
i |
z=p |
i |
где res X (z)zn−1 – вычет подынтегральной функции в полюсе z=pi
z=pi
Пусть a – полюс порядка m , тогда
|
1 |
|
(m−1) |
|
|
res f (z) = |
lim |
d |
|
[(z −a)m f (z)] |
|
|
|
|
|||
a |
(m −1)! z→a dzm−1 |
|
|||
Если полюс простой |
res X (z)zn−1 = lim[(z − pi ) X (z)zn−1 ] |
||||
|
|
z=pi |
|
z→pi |
|
2. Разложение X (z) на простые дроби.
Например, для рационального z–преобразования с однократными полюсами X(z) можно представить в форме
N |
|
Ai |
|
|
|
|
N |
|
X (z) = ∑ |
|
|
|
, тогда x(n) = ∑Ai pin для всех n. |
||||
1− pi z |
−1 |
|||||||
i=1 |
|
|
|
i=1 |
||||
простая дробь |
|
Ai |
→ A pn |
последовательность |
||||
1− p z−1 |
||||||||
|
|
i i |
|
|||||
|
|
|
|
i |
|
|
||

3. Разложение X (z) в степенной ряд.
Если z–преобразование имеет вид степенного ряда, можно заметить, что значение x(n) последовательности есть коэффициент при z-n в этом ряде
∞
X (z) = ∑x(n)z−n .
n=0
X (z) = x(0)z−0 + x(1)z−1 + x(2)z−2 +...
X (z) = x(0) + x(1)z−1 + x(2)z−2 +...
Если X(z) дается в замкнутом виде, то часто можно вывести соответствующий степенной ряд или использовать известное разложение в ряд.
Например, представление в виде степенного ряда можно получить
непосредственным делением числителя на знаменатель
X (z) = 6z2 −4z1 +2 z2 + z −1
Передаточная (системная) функция
x (n ) |
h ( n ) |
y (n ) |
||||
Л П П – система |
||||||
|
|
|
|
|
||
|
|
|
(цифровой |
|
|
|
|
|
|
|
|
||
|
|
|
фильтр) |
|
|
|
|
|
|
|
|
|
|
Z −пр
на входе x[n] X (z)
Z −пр
на выходе y[n] Y (z)
Z −пр
импульсная характеристика h[n] H (z)
Свойство свертки Z-преобразования
∞
Последовательность y[n] = x[n] h[n] = ∑x[m]h[n −m] - свертка
имеет Z-преобразование Y (z)= X (z)H (z) m=−∞
Н(z) = Y (z)
X (z)
Н(z) – передаточная (системная) функция ЛПП-системы (цифрового фильтра)
9
Если систему можно описать линейным разностным уравнением с постоянными коэффициентами, то ее передаточная функция является отношением полиномов.
Разностное уравнение N-гo порядка
N |
M |
∑a(k) y(n −k) = ∑b(k)x(n −k) |
|
k =0 |
k =0 |
Применяя z-преобразование к обеим частям разностного уравнения с учетом свойства линейности и свойства задержки, получим
N |
|
|
|
M |
|
|
|
|
|
∑a(k)z−kY (z) = ∑b(k)z−k X (z) |
|
|
|
||||||
k =0 |
|
|
|
k =0 |
|
|
|
|
|
|
N |
|
|
M |
|
|
|
||
Y (z) ∑a(k)z−k = X (z) |
∑b(k)z−k |
|
|
|
|||||
k =0 |
|
|
k =0 |
|
|
|
|||
|
|
|
|
M |
|
|
M |
|
|
|
|
Y (z) |
|
∑b(k)z |
−k |
∑b(k)z−k |
|
|
|
H (z) = |
|
= |
k =0 |
|
или H (z) = |
k =0 |
|
, a(0) =1 |
|
|
X (z) |
N |
|
N |
|
||||
|
|
|
∑a(k)z |
−k |
1+∑a(k)z |
−k |
|||
|
|
|
|
k =0 |
|
|
k =1 |
|
|
Эта формула дает конкретное выражение для передаточной функции, и коэффициенты полиномов в числителе и знаменателе являются соответственно
коэффициентами в правой и левой частях разностного уравнения.
Понятие нуля и полюса функции
Нуль функции y = f (x) – значение аргумента xн , при котором функция обращается в нуль, т.е. y = f (xн) = 0 .
Полюс функции y = f (x) – значение аргумента |
xп , при котором функция |
|||||||||||||
обращается в бесконечность, т.е. y = f (xп) = ∞ |
|
|
|
|
|
|
|
|||||||
Для передаточной функции |
|
|
|
|
|
|
|
|
|
|
||||
|
M |
|
|
M |
|
|
|
|
|
|
|
|
|
|
H (z) = |
∑b(k)z−k |
= |
|
∑b(k)z−k |
|
= |
b(0) +b(1)z |
−1 |
+... +b(М)z |
−М |
||||
k =0 |
|
k =0 |
|
|
|
|
||||||||
N |
|
N |
|
|
1 + а(1)z |
−1 |
+... + а(N )z |
−N |
||||||
|
∑a(k)z−k |
|
1 + ∑a(k)z |
−k |
|
|
|
|
|
|
||||
|
k =0 |
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
Нуль передаточной функции – корни (z=zi) уравнения, стоящего в числителе
H (z) .
Полюс передаточной функции – корни (z=pi) уравнения, стоящего в знаменателе H (z) .
Так как выражение H(z) есть отношение полиномов от z –1, то его можно записать в виде
M
∏(1− zi z−1 )
H (z) = A iN=1
∏(1− pi z−1 )
i=1
Каждый из сомножителей (1 – ziz-1) в числителе дает нуль при z =zi и полюс при
z=0.
Каждый сомножитель (1 – piz-1) в знаменателе дает полюс при z=pi и нуль в начале координат.
Следовательно, с точностью до скалярного может быть полностью описана картиной (обозначение: нуль – кружок, полюс – крестик).
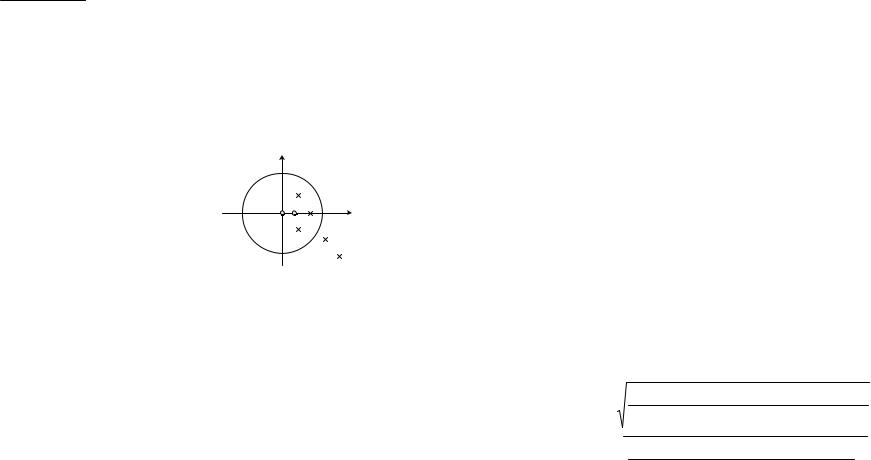
Картина нулей и полюсов в Z-плоскости
множителя А передаточная функция
полюсов и нулей в z-плоскости.
j y |
Z - пл. |
-1 |
1 |
|
x |
Если система устойчива, то все полюсы должны лежать внутри единичного круга и область сходимости будет содержать единичную окружность.
По этой причине при описании передаточной функции диаграммой полюсов и нулей в z-плоскости удобно изображать также единичную окружность, чтобы было видно расположение полюсов относительно этой окружности.
В частном случае, когда N=0 (КИХ-фильтр, нерекурсивный фильтр), система не имеет полюсов, за исключением точки z=0, и ее импульсная характеристика имеет конечную длительность.
M |
|
|
|
|
|
|
H (z) = ∑b(k)z−k |
x(n) |
|
x(n-1) |
|||
k =0 |
|
|||||
z -1 |
||||||
Элемент задержки |
|
|
|
|
||
|
|
|
|
|||
|
|
|
|
|
||
H (z) = z−1 – передаточная функция элемента задержки на один отсчет
При N>0 (БИХ-фильтр, рекурсивный фильтр) система имеет полюсы, каждый из которых прибавляет экспоненциальную последовательность к импульсной характеристике.
Таким образом, если передаточная функция имеет полюсы, то импульсная
10
Общие свойства передаточной функции.
|
|
|
M |
|
|
|
|
M |
|
|
|
|
|
|
|
|
H (z) = |
Y (z) |
= |
∑b(k)z−k |
= |
∑b(k)z−k |
|
|
|
|
|||||||
k =0 |
|
k =0 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
X (z) |
|
N |
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
∑a(k)z−k |
|
1+∑a(k)z−k |
|
|
|
|
||||||||
|
|
|
k =0 |
|
|
|
|
k =1 |
|
|
|
|
|
|
|
|
H (z) = |
Y (z) |
= |
b |
+b z−1 |
+b z−2 |
+... +b |
z−M |
, |
a |
|
=1 |
|||||
|
0 |
1 |
|
2 |
|
|
M |
|
|
0 |
||||||
X (z) |
1+a z−1 |
|
|
|
+... +a |
|
z−N |
|||||||||
|
|
+a |
z−2 |
N |
|
|
|
|||||||||
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
Частотные характеристики.
Комплексная передаточная функция дискретной цепи (частотная характеристика) связана с передаточная (системной) функция дискретной цепи
H ( jω) = H (Z ) | |
jωT или H ( jω) = H (Z ) | |
jω |
|
|
||||||
Z =e |
|
|
|
|
|
|
Z =e |
|
|
|
Передаточная функция дискретной цепи |
|
|
|
|
||||||
H (z) = |
Y (z) |
= |
b |
+b z−1 |
+b z−2 |
+... +b |
z−M |
|||
|
0 |
1 |
2 |
|
M |
|
||||
X (z) |
1+a z−1 |
|
+... +a |
|
z−N |
|||||
|
|
|
+a |
z−2 |
N |
|||||
|
|
|
|
|
1 |
2 |
|
|
|
|
Комплексная передаточная функция (частотная характеристика)
H ( jω) = |
b +b e− jωT +b e− j 2ωT +... +b |
|
e− jMωT |
|||||
0 |
1 |
2 |
|
M |
|
|||
|
1 + a e− jωT + a |
e− j 2ωT +... + a |
e− jNωT |
|||||
|
|
1 |
2 |
|
|
N |
|
|
Модуль H ( jω) |
- H (ω) = mod[H ( jω)] |
|
– АЧХ, |
|||||
Аргумент H ( jω) |
- ϕ(ω) = arg[H ( jω)] |
|
|
|
– ФЧХ. |
|||
H (ω) = |
(b |
+b cos ωT +.. +b |
|
cos MωT )2 + |
||||
0 |
1 |
|
M |
cos NωT )2 + |
||||
|
(1+a cos ωT +.. +a |
N |
||||||
АЧХ |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+(b1 sin ωT +... +bM sin MωT )2
+(a1 sin ωT +... +aN sin NωT )2
|
ϕ(ω) = −arctg |
|
|
b1 sin ωT +.. +bM sin MωT |
|||
|
b +b cos ωT +... +b |
cos MωT |
|||||
ФЧХ |
0 |
1 |
M |
|
|
||
|
|
|
a1 sin ωT +.. +aN sin NωT |
||||
|
+arctg |
|
|||||
|
1 |
+a cos ωT +.. +a |
N |
cos NωT |
|
||
|
|
|
|
1 |
|
|
|
характеристика имеет бесконечную протяженность.
