Illyustratsii_k_lektsiam_TsOS

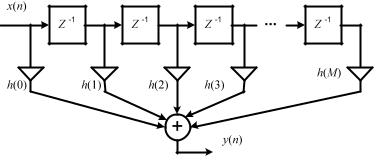
Все рассмотренные формы реализации РЦФ при одних и тех же входных данных и бесконечной разрядности представления чисел в ЦФ дают абсолютно одинаковые результаты, т.к. получены путем эквивалентных математических преобразований одного и того же исходного уравнения.

Передаточная функция рекурсивного фильтра

1 ak z k

k 1

Однако, при ограниченной разрядной сетки представления чисел, что всегда имеет место в реальных ЦФ, эти формы приведут к различному результату, т.к. отличаются механизмом преобразования погрешностей округления.

Основные структурные схемы при построении КИХ-фильтров

Передаточная функция

n 0

Это означает, что если длина импульсной характеристики равна N отсчетам, то H(z) является полиномом по z-1 степени N-1.

Поэтому Н(z) имеет N-1 полюсов в точке z=0 и N-1 нулей, которые могут быть в любом месте ограниченной z-плоскости.

Прямая форма

k 0

прямая форма построения КИХ-фильтров является частным случаем прямой формы БИХ-фильтров

Прямая форма построения КИХ-фильтра.

Структурная схема, показанная на рисунке, является реализацией соотношения (10) и соответствует прямому порядку выполнения сложений и умножений.

Из-за сходства этой структуры с линией задержки с отводами ее часто называют фильтром с многоотводной линией задержки

(или трансверсальным фильтром).

Каскадная форма и структура на основе быстрой свертки

В отличие от прямой формы построения структур при каскадной форме предполагается, что передаточная функция представляется в виде произведения сомножителей второго порядка, т. е.

k 1

если N - четное, то один из коэффициентов bk(2) будет равен нулю в связи с тем, что для четных N приведенное уравнение передаточной функции H(z) имеет нечетное число действительных корней.

Каскадная форма построения КИХ-фильтра.

Для построения фильтров без полюсов довольно часто применяют еще несколько структур, которые не имеют аналогов с фильтрами общего вида, содержащими и нули, и полюсы.

Наиболее распространенная из них основана на так называемом методе быстрой свертки, когда свертка вычисляется с помощью обратного преобразования Фурье от произведения преобразований Фурье входной последовательности и импульсной характеристики системы.

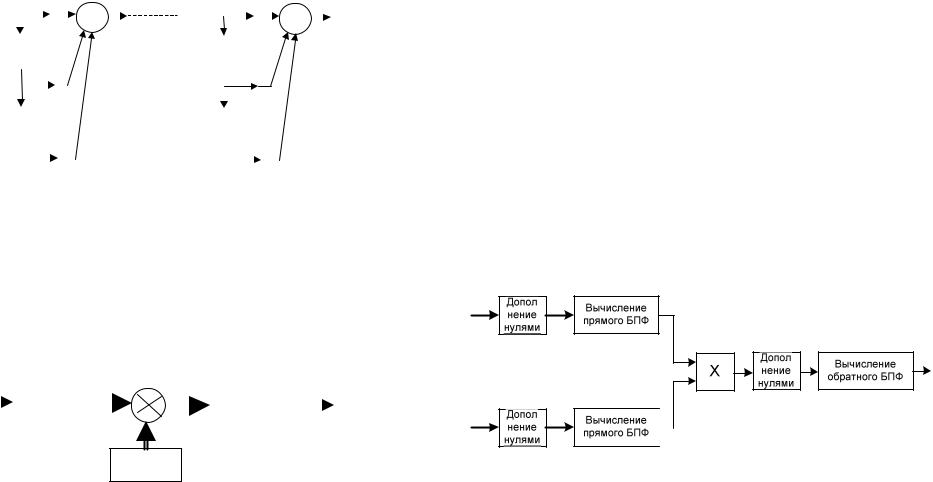
Структура КИХ-фильтра на основе быстрой свертки

Свертка – основной процесс в цифровой обработке сигналов. Поэтому важно уметь эффективно ее вычислять. Прямое вычисление свертки требует N*M умножений, где N – длина исходного сигнала, а M

– длина ядра свертки. Часто длина ядра свертки достигает нескольких тысяч точек, и число умножений становится огромным.

Однако существует алгоритм, позволяющий вычислить свертку значительно быстрее. Этот алгоритм основан на следующей важной теореме (свойство свертки z -преобразования), которую приведем в нестрогой формулировке:

Теорема свертки:

свертка во временной области эквивалентна умножению в частотной области; умножение во временной области эквивалентно свертке в частотной области.

Это значит, что для выполнения свертки двух сигналов можно перевести их в частотную область, умножить их спектры и перевести их обратно во временную область.

Такая операция выглядит громоздко.

Однако с появлением алгоритмов БПФ, позволяющих быстро вычислять преобразования Фурье, вычисление свертки через частотную область стало широко использоваться.

При значительных длинах ядра свертки такой подход позволяет в сотни раз сократить время вычисления свертки.

Быстрая свертка на основе БПФ.

ДПФ

y n x n *h n Y k X k H k

Алгоритм вычисления быстрой свертки

X д (k)

Hд (k)

Кратко опишем алгоритм вычисления быстрой свертки.

Сначала исходный сигнал длины N и ядро свертки длины M дополняются (справа) нулями до длины L (L – степень двойки), причем так, что L ≥ N + M −1.

Затем вычисляются ДПФ этих двух сигналов, при этом получаются комплексные спектры.

Затем спектры сигналов необходимо перемножить (используется перемножение комплексных чисел), при этом получается новый спектр также состоящий из комплексных коэффициентов.

Затем из полученного спектра с помощью обратного ДПФ вычисляется сигнал, состоящий из L точек.

Этот сигнал и содержит результат свертки из N+M-1 точек, дополненный нулями до L точек.

Структуры с частотной выборкой

Ранее было показано, что z-преобразование последовательности конечной длины N может быть представлено с помощью N отсчетов, равномерно распределенных на единичной окружности.

Для КИХ-фильтра передаточная функция может быть представлена как

называются частотными выборками, так как они являются просто выборками (отсчетами) частотной характеристики системы.

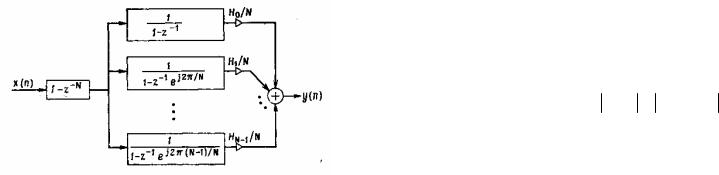
Структура КИХ-фильтра с частотной выборкой.

Выражение (12) означает, что КИХ-система может быть реализована как каскадное соединение простой КИХ-системы и БИХ-

Часть структуры, соответствующая БИХ-системе, состоит из параллельного соединения N комплексных систем первого порядка с

2

полюсами в точках zk e j N k .

Эти системы первого порядка имеют полюсы, лежащие строго на единичной окружности, назначение которых заключается в подавлении точно одного из нулей КИХ-системы.

На практике трудности обеспечения устойчивости, обусловленные расположением нулей на единичной окружности, исключаются с помощью образования выборок передаточной функции H(z) на

окружности радиуса r, где r=1–(2-12 2-16) немного меньше единицы.

В этом случае Н(z) представляется как

где для точного представления H(z) с помощью (14) требуется, чтобы

Если значение r выбрано близким к единице, то появляется небольшая ошибка, когда вместо выражения (15) используется (13).

В общем случае частотные выборки H(k) являются комплексными, поэтому реализация КИХ-систем, таких, как на рисунке, требует комплексных арифметических операций.

Однако, если отсчеты импульсной характеристики h(п) являются действительными, то частотные выборки, выраженные в полярных координатах, удовлетворяют следующим условиям симметрии:

H (k) H (N k);

(k) (N k), k 0,1,2,...N 1,

где если H(0)>0, то (0) = 0. Кроме того, поскольку

то цепи первого порядка образуют комплексно-сопряженные пары, за

исключением цепи с полюсом в точке ej(2 /N)0 = 1, и для N четного – цепи с полюсом в точке ej(2 /N)N/2= –1.

Следовательно, комплексные цепи первого порядка могут быть сгруппированы в комплексно-сопряженные пары и выполнены как цепи второго порядка с действительными коэффициентами, как это было показано в примере 3 раздела 4.1.

Существуют два принципиальных преимущества реализаций на основе частотной выборки.

Первое заключается в том, что в умножителях на выходах каждой системы второго порядка используются величины, пропорциональные отсчетам частотной характеристики, равномерно распределенным по углу на единичной окружности. Эти величины могут, конечно, быть получены из ДПФ импульсной характеристики.

Если подлежащий выполнению фильтр является частотноизбирательным с одной или более полосой непропускания, то он может быть спроектирован так, чтобы частотные выборки в полосе непропускания были нулевыми, что уменьшает число подлежащих реализации систем второго порядка.

Если большинство частотных отсчетов являются нулевыми, как в случае узкополосного низкочастотного или полосового фильтра, то структура на основе частотной выборки может потребовать меньше умножений, чем прямая форма построения.

Конечно, реализация на основе частотной выборки будет всегда требовать большую память, чем прямая форма построения.

Второе преимущество следует из того, что полюсы и нули структуры фильтра зависят только от длины импульсной характеристики.

Если входной сигнал подлежит обработке с помощью банка КИХфильтров (т. е. нескольких различных импульсных характеристик длиной N), то одна реализация множителя (1–z-N) и каждого блока второго порядка будет служить для всех фильтров.

Кроме того, структура состоит из одинаковых функциональных блоков второго порядка, что дает возможность реализации этих блоков последовательно во времени.

Свойства цифровых КИХ-фильтров

Перечислим основные достоинства КИХ-фильтров:

1.Легко создавать КИХ-фильтры со строго линейной фазовой характеристикой.

Во многих случаях, когда проектируется фильтр с произвольной амплитудной характеристикой, это упрощает задачу аппроксимации.

Фильтры с линейной фазовой характеристикой особенно важны в случаях, когда приходится учитывать дисперсионные искажения, связанные с нелинейностью фазовой характеристики (например, при обработке речи и передаче данных).

2.КИХ-фильтры можно эффективно строить как по рекурсивной, так и по нерекурсивной схемам.

3.КИХ-фильтры, реализуемые нерекурсивно, т.е. с помощью прямой свертки, всегда устойчивы.

Передаточная функция физически реализуемого КИХ-фильтра имеет вид

N 1

H (z) h(n)z n

n0

Это означает, что если длина импульсной характеристики равна N отсчетам, то H(z) является полиномом по z-1 степени N-1.

Поэтому Н(z) имеет N-1 полюсов в точке z=0 и N-1 нулей, которые могут быть в любом месте z-плоскости.

n0

Сфазо-частотной характеристикой фильтра ( ) связаны такие понятия как фазовая p и групповая g задержки, определяемые соотношениями:

Для обеспечения постоянства фазовой p и групповой g задержек ФЧХ фильтра должна быть линейной функцией частоты , т.е. ( ) = - .

Во многих приложениях требуется постоянство только групповой задержки и, следовательно, ФЧХ может иметь вид ( ) = 0 - , где0 – постоянная величина.

Если импульсная характеристика удовлетворяет условию симметрии

или антисимметрии, т.е.

h(n) h(N 1 n), n 0,1, 2, ... N (*) то КИХ-фильтр имеет линейную ФЧХ.

Для центрированной импульсной характеристики h0(n),

удовлетворяющей соотношению h0(n)=h(n+(N-1)/2)

или h(n)=h0(n-(N-1)/2),

Условие линейности ФЧХ фильтра можно записать в виде: h0(n)= h0(-n)

т.е. необходима четная или нечетная симметрия центрированной импульсной характеристики h0(n).

Целесообразно рассмотреть условия (*) раздельно для четного и нечетного N.

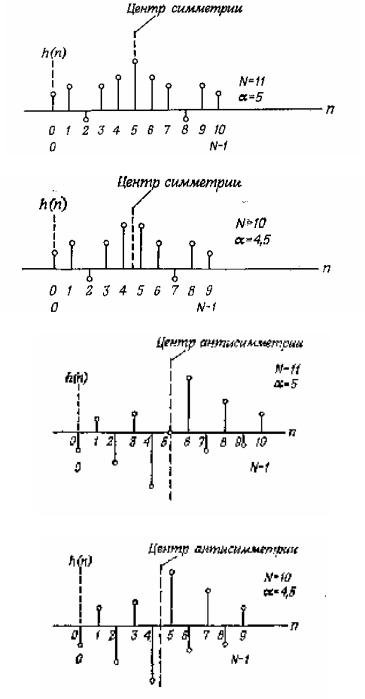
Типичные импульсные характеристики фильтра с линейной ФЧХ представлены на рисунках (=(N-1)/2):

а) нечетное N=11 (четная симметрия);

б) четное N=10 (четная симметрия);

в) нечетное N=11 (нечетная симметрия);

г) четное N=10 (нечетная симметрия).

а) нечетное N (четная симметрия);

б) четное N (четная симметрия)

в) нечетное N (нечетная симметрия)

г) четное N (нечетная симметрия)

Фильтр вида 4.

Антисимметричная импульсная характеристика, четное N.

Таким образом, и в этом случае H 0 (e j ) - чисто мнимая функция

частоты . Кроме того, всегда H0(ej0)=0.

Поэтому этот вид фильтров наиболее пригоден для проектирования преобразователей Гильберта и дифференциаторов.

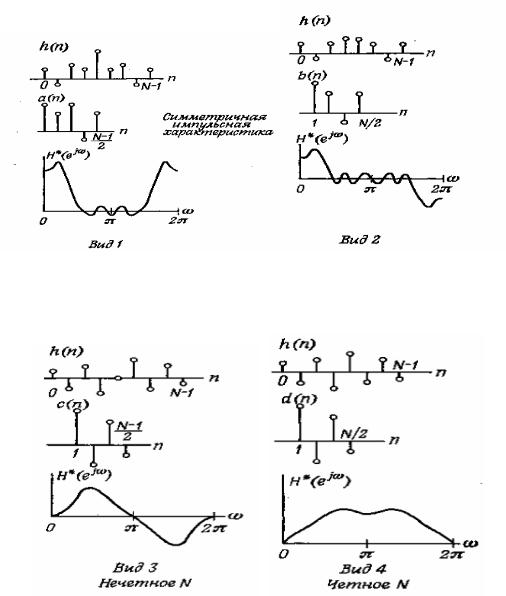
На рисунке графически представлены типичные импульсные характеристики h(n), соответствующие им последовательности (от a(n) до d(n) для каждого конкретного случая) и типичные частотные

характеристики H (e j ) для каждого из четырех видов КИХ-фильтров с линейной ФЧХ.

Четыре вида фильтров с линейной ФЧХ.

Симметричная импульсная характеристика

Антисимметричная импульсная характеристика