
Mat_Analiz_Prokhorov
.pdfТеорема 4. Пусть функции f и g дифференцируемы на отрезке [a, b] и по крайней мере одно из двух произведений f g или fg имеет первообразную на [a, b]. Тогда второе из этих двух произведений также имеет первообразную на [a, b] и справедлива формула интегрирования по частям
b b
( f ' g )(x)dx ( fg)(b) ( fg )(a) ( fg' )(x)dx.
a a
Доказательство. Произведение fg дифференцируемых функций f и g дифференцируемо и справедлива формула
(fg) (x) = (f g)(x) + (fg )(x).
Предположим, что произведение fg имеет первообразную H на отрезке [a, b]. В случае, когда f g имеет первообразную, рассуждения симметричны. Перепишем формулу производной произведения в виде
(f g)(x) = (fg) (x) (fg )(x).
Из того, что функция (fg) имеет первообразную fg и произведение fg имеет первообразную H на [a, b], по теореме 2 следует, что произведение f g имеет первообразную на [a, b], которую обозначим через E, и справедлива формула
E(x) = (fg)(x) H(x).
Подставим в эту формулу x = b и x = a и после вычитания второго выражения из первого получим
b
( f ' g )(x)dx E(b) E(a) ( fg )(b) ( fg )(a) (H (b) H(a))
a
b
( fg (b)) ( fg)(a) ( fg ')(x)dx,
a
201
что заканчивает доказательство теоремы 4.
Если в теореме 4 рассматривать значение b как переменную величину, то теорема 4 представляет инструмент интегрирования по частям в задаче о нахождении первообразных.
4. Замена переменной в определенном интеграле
Прочтение в обратном порядке формулы производной композиции дифференцируемых функций приводит к следующему правилу, называемому заменой переменной, или подстановкой.
Теорема 5. Пусть функция y = f(x) имеет первообразную на отрезке [a, b], а функция x = (t) дифференцируема на отрезке [ , ] и отображает отрезок [ , ] на отрезок [a, b] так, что ( ) = a и ( ) = b. Тогда функция y = f( (t)) (t) имеет первообразную на [ , ] и справедлива формула замены переменной
b
f (x)dx f ( (t)) ' (t)dt.
Доказательство. Пусть функция f имеет первообразную F на отрезке [a, b]. Это значит, что функция F дифференцируема на отрезке [a, b] и на этом отрезке справедливо равенство
F (x) = f(x).
Условия теоремы 5 обеспечивают корректное определение композиций функций f° и F° . Поскольку каждая из функций F
и дифференцируема на своей области определения, то и их композиция дифференцируема на отрезке [ , ] и справедлива формула
(F( )) (t) = F ( (t)) (t) = f( (t)) (t).
Из того, что функция y = (F( )) (t) имеет первообразную F° на отрезке [ , ] следует, что и функция y = f( (t)) (t) имеет
ту же первообразную на [ , ]. Следовательно, подставляя в y = F( (t)) значения t = и t = и вычитая второе выражение из первого, получим
202
F( ( )) F( ( )) f ( (t)) ' (t)dt.
Так как
F( ( )) F( ( )) F(b) F(a) b f (x)dx,
a
то две последние формулы приводят к формуле замены переменной в определенном интеграле, что заканчивает доказательство теоремы 5.
Если в теореме 5 рассматривать значения b и как переменные величины, то теорема 5 представляет инструмент замены переменной, или подстановки в задаче о нахождении первообразных.
203
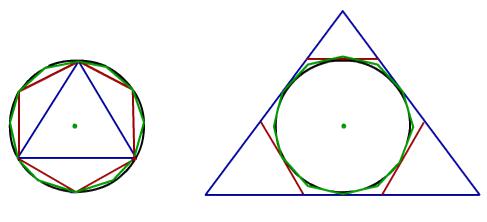
Лекция 20.
1. Геометрический подход в теории интеграла
2. Интеграл от характеристических функций
3. Интеграл от ступенчатых функций
4. Свойства интеграла от ступенчатых функций
1. Геометрический подход в теории интеграла
Геометрический подход в теории интеграла известен со времен Древней Греции, где научились вычислять площадь круга, длину окружности, объемы шара, конуса и других фигур, отличных от многогранника.
В программе современной школы объяснение способов этих вычислений также вполне научно и одновременно классично. Так например, площадь круга воспринимается как предел площадей вписанных в круг правильных многоугольников при неограниченном удвоении их сторон и равный ему предел площадей описанных правильных многоугольников при неограниченном удвоении их сторон.
Рис. 1. Удвоение сторон вписанных и описанных многоугольников
204

Многоугольники, вписанные в окружность или описанные около нее, выбраны не только потому, что они допускают технически реализуемый алгоритм вычисления площади, а еще и потому, что нет других фигур с вычисляемой площадью.
В самом деле, полагая по определению, что площадь квадрата со стороной 1 равна 1, мы приходим к выводу, что площадь квадрата со стороной a равна a2, а площадь прямоугольника со сторонами a и b равна ab. Отсюда нетрудно вывести формулу площади треугольника и фигуры, составленной из треугольников, - многоугольников.
Рис. 2. Площади фигур, составленных из треугольников В математическом анализе геометрический подход воплощается в идее вычисления площади фигуры, ограниченной
графиком функции и осевыми отрезками. Предположим, что функция f определена и положительна на отрезке [a, b], и поставим задачу вычисления площади фигуры, ограниченной графиком функции f, отрезком [a, b] на оси OX и отрезками, параллельными оси OY. Эту фигуру уместно назвать криволинейной трапецией или даже прямоугольной криволинейной трапецией, поскольку граница фигуры состоит из трех отрезков, два из которых параллельны, а третий им перпендикулярен, и линии графика.
205
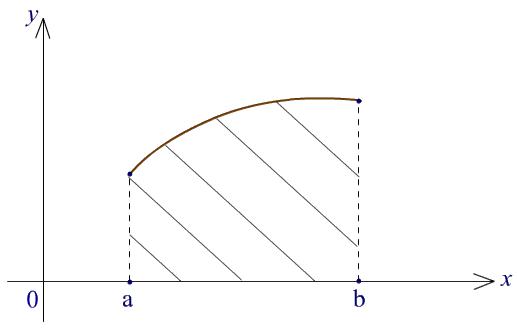
Рис. 3. Криволинейная трапеция Поддержим идею приближения фигуры многоугольниками изнутри и извне. Вид криволинейной трапеции подсказывает вид
многоугольников - прямоугольники со сторонами, параллельными оси OY, и с одним из оснований, расположенным на оси
OX.
206
|
|
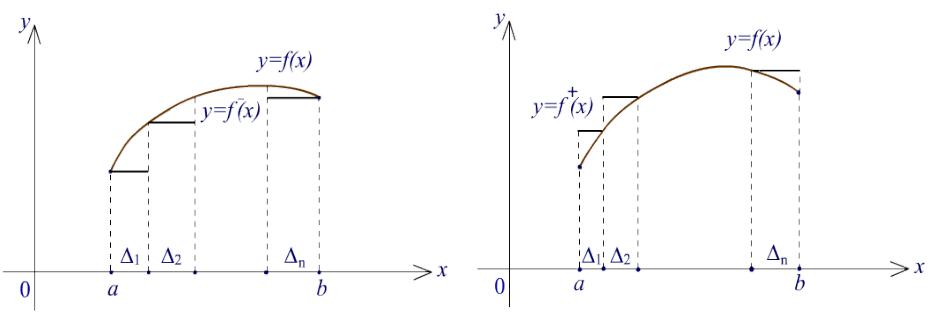
Рис. 4. Приближение криволинейной трапеции |
Рис. 5. Приближение криволинейной трапеции |
многоугольниками изнутри |
многоугольниками извне |
Переведем геометрическую идею на язык математического анализа. Построение вписанных прямоугольников означает разбиение отрезка [a, b] на части 1, 2, ..., n и проведение верхних сторон прямоугольников, которые образуют график некоторой функции f , постоянной на каждом из 1, 2, ..., n. Так как верхние стороны прямоугольников расположены ниже графика функции f, то f f. Построение описанных прямоугольников, верхние стороны которых расположены выше графика функции f, приводит к созданию функции f , постоянной на каждом из 1, 2, ..., n, и такой. что f f.
Площадь криволинейной трапеции должна восприниматься одновременно как верхняя грань сумм площадей всех вписанных в нее прямоугольников и как нижняя грань сумм площадей всех описанных около нее прямоугольников.
2. Интеграл от характеристических функций
Сначала дадим определение характеристической функции множества.
207
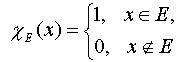
Определение 1. Пусть E . Функция E, задаваемая формулой
называется характеристической функцией множества E.
Очевидны формулы, связывающие теоретико-множественные операции и арифметические операции над характеристическими функциям
A B = A B,
A B = A + B A B
и если B A, то
A\B = A B.
208
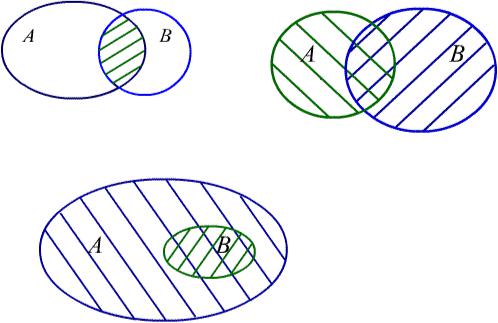
Рис. 6. Соотношения между множествами.
Начнем аналитическую реализацию геометрического подхода с описания функций, график которых является верхней
стороной прямоугольника высоты 1. Будем рассматривать четыре типа множеств , лежащих в основании прямоугольника: отрезки, интервалы и полуотрезки (полуинтервалы)
(1) [a, b], (a, b), [a, b), (a, b].
В частности, если a = b, то отрезок [a, a] вырождается в точку {a}. Графиком характеристической функции является отрезок на высоте 1, расположенный над , и часть оси OX, находящейся вне .
209

Рис. 7. График характеристической функции множества .
Определение 2. Пусть - одно из множеств (1). Тогда число (b a) называется интегралом Римана от характеристической функции и обозначается
(x)dx
Число (b a) численно выражает площадь прямоугольника P высоты 1 с основанием . Различие между типами множества состоит в том, что одна или обе боковые стороны прямоугольника P могут принадлежать или не принадлежать P. Это различие не сказывается на площади прямоугольника P, поскольку площадь отрезка, являющегося боковой стороной прямоугольника, равна нулю.
210
