Mat_Analiz_Prokhorov

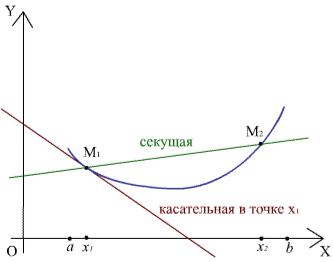
Рис. 10. Геометрическая интерпретация выпуклости

График дифференцируемой функции имеет касательную в каждой точке. Через точки M1 и M2 на графике дифференцируемой выпуклой функции проведем прямую, называемую секущей. Хорда M1M2 составляет часть секущей и находится не ниже стягиваемой ею дуги графика. Если x2 устремить к x1, то секущая устремится к касательной к графику в точке x1, хорда M1M2 выродится в точку касания и касательная окажется целиком не выше графика. Таким образом, дифференцируемая функция выпукла тогда и только тогда, когда ее график расположен не ниже касательной в любой точке.

4. Точка перегиба функции

Определение выпуклой функции основано на свойстве выпуклости ее надграфика. Если вместо выпуклости надграфика предположить выпуклость множества, расположенного под графиком функции, то придем к симметричному геометрическому определению свойства функции, зачастую называемому вогнутостью. Аналитическое выражение определения вогнутости сведется к повторению определения 6 с заменой в нем знака неравенства на противоположный. Очевидно, что по аналогии с теоремой 1 и следствием 1 критерий вогнутости дифференцируемой функции означает

противоположный характер монотонности f или справедливость неравенства f (x) 0 для дважды дифференцируемой функции f.

Естественно, что произвольная функция в некоторых точках может менять характеристики своего поведения, включая переход от выпуклости к вогнутости или обратно.

191

Рис. 11. Точка перегиба.

Определение 7. Пусть функция f определена на отрезке [a, b] и x0 (a, b). Если функция f выпукла на одном из отрезков [a, x0] или [x0, b] и вогнута на другом, то точка x0 называется точкой перегиба функции f.

5. Необходимое условие точки перегиба

Теорема 1 и ее следствие 1 дают быстрое решение задачи о необходимом условии точки перегиба.

Теорема 2. (Необходимое условие точки перегиба). Пусть функция f дифференцируема на [a, b] и дважды дифференцируема в точке x0 (a, b). Если x0 является точкой перегиба функции f, то f (x0) = 0.

Доказательство. В силу теоремы 1 производная f меняет характер монотонности при переходе через точку x0. Поэтому f (x) - f (x0) не меняет знака в окрестности точки x0, а следовательно,

имеет в этой окрестности разные знаки при x < x0 и x > x0. Значит, равные между собой значения

192

и 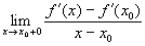не могут иметь одинаковых знаков, то есть

что доказывает теорему 2.

193

Лекция 19

1. Первообразная. Множество первообразных данной функции

2. Неопределенный и определенный интегралы

3. Интегрирование по частям определенного интеграла

4. Замена переменной в определенном интеграле

1. Первообразная. Множество первообразных данной функции

Действие дифференцирования функции на интервале (a, b) можно истолковать как операционное действие f f , сопоставляющее каждой дифференцируемой на (a, b) функции f ее производную f . В таком смысле естественно рассчитывать на возможность обратного сопоставления f f, которому дадим специальное название.

Определение 1. Функция F называется первообразной функции f на интервале (a, b), если F дифференцируема и для всех x (a, b) выполняется равенство

F (x) = f(x).

Очевидно, что понятие первообразной является обратным по отношению к производной, а операцию отыскания

первообразной разумно воспринимать как сопоставление f F или F F, то есть действие, обратное к дифференцированию.

Определение 1 распространяется и на отрезок [a, b] с той оговоркой, что значение F в крайних точках a и b понимается односторонне:

194

Покажем, что первообразная определяется неоднозначно, но множество всех первообразных данной функции устроено довольно просто.

Теорема 1. Если функция f имеет первообразную F на интервале (a, b), то множество всех первообразных функции f на (a, b) имеет вид

{F + C: C }.

Доказательство. Смысл теоремы состоит в том, что если F - первообразная функции f, то F + C, где C - произвольное действительное число, также является первообразной функции f и других первообразных функция f не имеет.

Докажем сначала первое утверждение. Пусть F является первообразной для f. Значит, функция F дифференцируема на (a, b) и на этом интервале выполняется равенство F (x) = f(x). Но тогда для любого действительного числа C также справедливо

равенство (F + C) (x) = F (x) = f(x), которое доказывает, что функция F + C также является первообразной функции f на (a, b).

Теперь покажем, что множество первообразных функции f вполне исчерпывается функциями F + C. Предположим, что функция G является первообразной для f. Значит, функция G дифференцируема на (a, b) и на этом интервале выполняется

равенство G (x) = f(x). Образуем функцию H = G f, которая дифференцируема на (a, b) и на этом интервале справедливо равенство

H (x) = F (x) G (x) = f(x) f(x) = 0.

Выберем произвольно точки x1 и x2 на (a, b), x1 < x2. Применим теорему Лагранжа к функции H на (a, b), согласно которой найдется точка c (x1, x2) такая, что справедлива формула

H(x2) H(x1) = H (c)(x2 x1).

Поскольку H (c) = 0, то и H(x2) H(x1) = 0. Это показывает, что во всех точках интервала (a, b) функция H принимает одинаковые значения, то есть H(x) = C для некоторого действительного числа C тождественно на (a, b). Возвращаясь к функциям F и G, приходим к формуле

195

G(x) = F(x) + C, x (a, b),

которая заканчивает доказательство теоремы 1.

Теми же рассуждениями устанавливаем, что теорема 1 справедлива и в применении к отрезку [a, b].

2. Неопределенный и определенный интегралы

Определение 2. Пусть функция f имеет первообразную на отрезке [a, b]. Тогда множество всех первообразных функции f на [a, b] называется неопределенным интегралом от функции f на [a, b] и обозначается

f (x)dx.

Теорема 1 показывает, что если F - одна из первообразных функции f на [a, b], то неопределенный интеграл является множеством функций F + C, где C - произвольное действительное число.

Более полезным является понятие определенного интеграла.

Определение 3. Пусть функция f имеет первообразную F на отрезке [a, b]. Тогда значение

F(b) F(a)

называется определенным интегралом от функции f на [a, b] и обозначается

b

f (x)dx.

a

Определение 3 корректно в том смысле, что оно не зависит от выбора первообразной. Действительно, пусть функция G также является первообразной функции f на [a, b]. Согласно теореме 1 G = F + C, где C - некоторое действительное число. Тогда

G(b) G(a) = (F(b) + C) (F(a) + C) = F(b) F(a),

196

что устанавливает корректность определения 3.

Покажем, что определенный интеграл обладает свойством линейности.

Теорема 2. Если функции f и g имеют на отрезке [a, b] первообразные, то функции f, , и f + g также имеют первообразные на [a, b] и справедливы формулы

b b

( f )(x)dx f (x)dx,

a a

b b b

( f g)(x)dx f (x)dx g(x)dx.

a a a

Доказательство. Пусть функция f имеет первообразную F, а функция g имеет первообразную G на отрезке [a, b]. Это значит, что F и G дифференцируемы на [a, b] и на этом отрезке справедливы формулы

F (x) = f(x), G (x) = g(x).

Следовательно, функции F и F + G также дифференцируемы на [a, b] и справедливы формулы

( F) (x) = F (x) = f(x), (F + G) (x) = F (x) + G (x) = f(x) + g(x).

Это означает, что функция F является первообразной функции f, а функция F + G является первообразной функции f + g и справедливы формулы

197

b

( f g)(x)dx (F G)(b) (F G)(a) F (b) F (a) G(b) G(a)

a

bb

f (x)dx g(x)dx,

aa

которые заканчивают доказательство теоремы 2.

Следующая теорема выражает свойство аддитивности определенного интеграла.

Теорема 3. Если функция f имеет первообразную на отрезке [a, b], то для любой точки c (a, b) функция f имеет первообразную на [a, c] и [c, b] и справедлива формула

b c b

f (x)dx f (x)dx f (x)dx.

a a c

Доказательство. Пусть функция f имеет первообразную F на отрезке [a, b]. Значит, F дифференцируема на [a, b] и на этом отрезке справедлива формула

F (x) = f(x).

Следовательно, F дифференцируема на любой части отрезка [a, b] и остается первообразной функции f на [a, c] и [c, b] и справедлива формула

198

что заканчивает доказательство теоремы 3.

Определение 3 рассматривает определенный интеграл только в случае, когда в знаке интеграла нижний предел строго меньше верхнего предела. Однако сама формула определения 3 делает естественным следующее соглашение: в случае a > b для функции f, имеющей первообразную на отрезке [b, a], будем считать, что

b a

f (x)dx f (x)dx,

ab

а в случае a = b будем считать, что

a f (x)dx 0.

a

Для нахождения первообразных элементарных функций мы располагаем основной таблицей производных, которую следует прочитать в обратном порядке:

xn 1

(xn 1 )' (n 1)xn xndx n 1 C, n 1;

(ex )' ex exdx ex ;

(log x)' 1x dxx log x C;

199

(sin x)' cos x cos xdx sin x C;

(cos x)' sin x sin xdx cos x C;

Расширение возможностей нахождения первообразных состоит в применении свойства линейности по теореме 2, а также попытке прочитать в обратном порядке формулы дифференцирования произведения функций и композиции функций, о чем пойдет речь в следующих частях лекции.

3. Интегрирование по частям определенного интеграла

Прочтение в обратном порядке формулы производной произведения дифференцируемых функций приводит к следующему правилу, называемому интегрированием по частям.

200