
-
Свойства собственных функций
В этой главе доказывается, что система
собственных функций краевой задачи
Штурма-Лиувилля
 полна
и образует ортогональный базис в
полна
и образует ортогональный базис в
 .
Теоремы о полноте и о разложении играют
важную роль при решении различных задач
математической физики методом разделения
переменных.
.
Теоремы о полноте и о разложении играют
важную роль при решении различных задач
математической физики методом разделения
переменных.
Теорема 2.1. (1) Система собственных
функций
 краевой задачи
краевой задачи
 полна в
полна в
 .
.
(2) Пусть
 ,
,
 - абсолютно непрерывная функция. Тогда
- абсолютно непрерывная функция. Тогда
|
|
(2.1) |
причем ряд сходится равномерно на

(3) Для
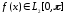 ряд (2.1) сходится в
ряд (2.1) сходится в
 ,
причем имеет место равенство Парсеваля
,
причем имеет место равенство Парсеваля
|
|
(2.2) |
Доказательство:
-
Обозначим

и рассмотрим функцию
 .
.
Функция
 называется функцией Грина задачи
называется функцией Грина задачи
 .
Она является ядром интегрального
оператора обратного к оператору
Штурма-Лиувилля, то есть функция
.
Она является ядром интегрального
оператора обратного к оператору
Штурма-Лиувилля, то есть функция
 дает решение краевой задачи
дает решение краевой задачи
|
|
(2.3) |
это легко проверяется дифференцированием. В самом деле


Так как
 ,
то
,
то

 ,
,
 ,
,

Учитывая (1.6) и используя теорему 1.2 вычисляем

В силу (1.8) имеем


|
|
(2.4) |
-
Пусть функция
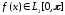 такова, что
такова, что
 .
.
Тогда с учетом (2.4)
 и, следовательно, при каждом фиксированном
и, следовательно, при каждом фиксированном
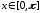 функция
функция
 является целой по λ. Получим теперь
оценку для
является целой по λ. Получим теперь
оценку для
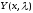 .
Ранее было получено
.
Ранее было получено


Используя представление для
 ,
вычисляем при
,
вычисляем при
 :
:

Получаем
 .
.
Используя принцип максимума модуля для
аналитических функций и теорему Лиувилля,
заключаем, что
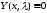 .
Отсюда, и из (2.3) следует, что
.
Отсюда, и из (2.3) следует, что
 на
на
 .
Таким образом, утверждение (1) доказано.
.
Таким образом, утверждение (1) доказано.
-
Пусть теперь
 - произвольная абсолютно непрерывная
функция. Так как
- произвольная абсолютно непрерывная
функция. Так как
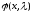 и
и
 - решения уравнения (1.1), то функцию
- решения уравнения (1.1), то функцию
 можно преобразовать к виду
можно преобразовать к виду

Интегрируем дважды по частям слагаемые со вторыми производными
 .
.
Подстановки в точках
 ,
,
 ,
,
 дают
дают
 ,
,
 ,
,
 .
.
Исходя из этого получаем
|
|
(2.5) |
где


Используя (1.9), (1.10) и (1.18), получаем при
фиксированном
 и достаточно большом
и достаточно большом

|
|
(2.6) |
Покажем, что
|
|
(2.7) |
Предположим сначала, что
 абсолютно непрерывна на
абсолютно непрерывна на
 .
В этом случае интегрирование по частям
дает
.
В этом случае интегрирование по частям
дает
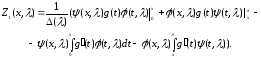
В силу (1.9), (1.10) и (1.18) получаем
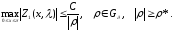
Пусть теперь
 .
Зафиксируем
.
Зафиксируем
 и выберем абсолютно непрерывную функцию
и выберем абсолютно непрерывную функцию
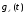 так, что
так, что

где

Тогда при
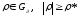 имеем
имеем
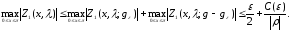
Следовательно, существует
 такое, что
такое, что
 при
при
 В силу произвольности
В силу произвольности
 приходим к (2.7).
приходим к (2.7).
Рассмотрим контурный интеграл
 ,
,
где
 (с обходом против часовой стрелки). Из
(2.5)-(2.7) вытекает
(с обходом против часовой стрелки). Из
(2.5)-(2.7) вытекает
|
|
(2.7) |
С другой стороны, можем вычислить
 с помощью теоремы о вычетах. В силу (2.4)
имеем
с помощью теоремы о вычетах. В силу (2.4)
имеем
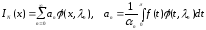 .
.
Сравнивая это с (2.8), приходим к (2.1), причем
ряд сходится равномерно на
 ,
то есть утверждение (2) доказано.
,
то есть утверждение (2) доказано.
-
Система собственных функций
 полна и ортогональна в
полна и ортогональна в ;
поэтому она образует ортогональный
базис в
;
поэтому она образует ортогональный
базис в
 и справедливо равенство Парсеваля
(2.2).
и справедливо равенство Парсеваля
(2.2).
-
Операторы преобразования.
Важную роль в теории обратных задач для
операторов Штурма-Лиувилля играют так
называемые операторы преобразования.
Они связывают решения двух различных
уравнений Штурма-Лиувилля при всех
 .
В этой главе мы построим операторы
преобразования, которые нам потребуются
в следующей главе.
.
В этой главе мы построим операторы
преобразования, которые нам потребуются
в следующей главе.
Теорема 3.1. Для функции
 имеет место представление
имеет место представление
|
|
(3.1) |
где
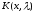 - вещественная непрерывная функция,
причем
- вещественная непрерывная функция,
причем
|
|
(3.2) |
Доказательство:
Из (1.11) при
 вытекает, что функция
вытекает, что функция
 является решением следующего интегрального
уравнения
является решением следующего интегрального
уравнения
|
|
(3.3) |
Так как
 ,
,
то (3.3) примет вид
 ,
,
и, следовательно,
 .
.
Метод последовательных приближений дает
|
|
(3.4) |
|
|
(3.5) |
Покажем по индукции, что
|
|
(3.6) |
где функции
 не зависят от
не зависят от
 .
.
Вычислим
 ,
используя соотношение
,
используя соотношение
 ,
,
получим

Замена переменных
 во втором интеграле дает
во втором интеграле дает
 .
.
Меняя порядок интегрирования во втором интеграле получаем

Таким образом (3.6) верно, при
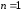 ,
где
,
где
|
|
(3.7) |
Предположим теперь, что (3.6) верно при
некотором
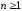 .
Тогда, подставляя (3.6) в (3.5), вычисляем
.
Тогда, подставляя (3.6) в (3.5), вычисляем

Замена переменных
 и
и
 соответственно приводят к равенству
соответственно приводят к равенству
 Меняя
порядок интегрирования, получаем
Меняя
порядок интегрирования, получаем

где
|
|
(3.8) |
Подставляя (3.6) в (3.4), приходим к (3.1), где
|
|
(3.9) |
Из (3.7) и (3.8) вытекает
 .
.
В самом деле, (3.7) дает при
 :
:
 .
.
Далее, если при некотором
 оценка для
оценка для
 верна, то в силу (3.8) имеем
верна, то в силу (3.8) имеем

Таким образом, ряд (3.9) сходится абсолютно
и равномерно при
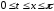 ,
и функция
,
и функция
 является непрерывной. Более того, из
(3.7)-(3.9) следует, что гладкость функции
является непрерывной. Более того, из
(3.7)-(3.9) следует, что гладкость функции
 совпадает с гладкостью функции
совпадает с гладкостью функции
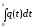 .
Так как согласно (3.7) и (3.8)
.
Так как согласно (3.7) и (3.8)
 ,
,
то приходим к (3.2). □
Оператор Т, определяемый формулой
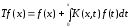 ,
,
отображает функцию
 ,
которая является решением уравнения
,
которая является решением уравнения
 с нулевым потенциалом, в функцию
с нулевым потенциалом, в функцию
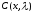 ,
которая является решением уравнения
(1.1) с некоторым потенциалом
,
которая является решением уравнения
(1.1) с некоторым потенциалом
 (то есть
(то есть
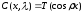 ).
Оператор Т называется оператором
преобразования для
).
Оператор Т называется оператором
преобразования для
 .
Важно, что ядро
.
Важно, что ядро
 не зависит от λ.
не зависит от λ.
Теорема 3.2. Для функций
 и
и
 имеют место представления:
имеют место представления:
|
|
(3.10) |
|
|
(3.11) |
где
 и
и
 - вещественные непрерывные функции с
той же гладкостью, что и функция
- вещественные непрерывные функции с
той же гладкостью, что и функция
 ,
причем
,
причем
|
|
(3.12) |
|
|
(3.13) |
Доказательство:
Функция
 удовлетворяет уравнению (1.24)
удовлетворяет уравнению (1.24)

Так
как
 ,
то
,
то
 ,
,
и, следовательно,
 .
.
Метод последовательных приближений дает
|
|
(3.14) |
|
|
(3.15) |
Покажем по индукции, что
|
|
(3.16) |
где функции
 не зависят от
не зависят от
 .
.
Вычислим
 ,
используя соотношение
,
используя соотношение
 ,
,
получим

Замена переменных
 во втором интеграле дает
во втором интеграле дает
 .
.
Меняя порядок интегрирования во втором интеграле получаем

Таким образом (3.16) верно, при
 ,
где
,
где
|
|
(3.17) |
Предположим теперь, что (3.16) верно при
некотором
 .
Тогда, подставляя (3.16) в (3.15), вычисляем
.
Тогда, подставляя (3.16) в (3.15), вычисляем

Замена переменных
 и
и
 соответственно приводят к равенству
соответственно приводят к равенству

Меняя порядок интегрирования, получаем

где
|
|
(3.18) |
Подставляя (3.16) в (3.14), приходим к (3.10), где
|
|
(3.19) |
Из (3.17) и (3.18) вытекает
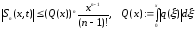 .
.
Доказательство, аналогично, доказательству
того, что
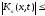
 из теоремы 3.1.
из теоремы 3.1.
Таким образом, ряд (3.14) сходится абсолютно
и равномерно при
 ,
и мы приходим к (3.10) и (3.13). Причем функция
,
и мы приходим к (3.10) и (3.13). Причем функция
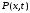 является непрерывной. Более того, из
(3.17)-(3.19) следует, что гладкость функции
является непрерывной. Более того, из
(3.17)-(3.19) следует, что гладкость функции
 совпадает с гладкостью функции
совпадает с гладкостью функции
 .
.
Соотношение (3.11) может быть получено прямо из (3.1) и (3.10):

где
 .
.
Полагая здесь
 ,
приходим к (3.12).
□
,
приходим к (3.12).
□


 .
.
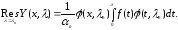

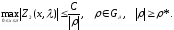


 ,
,
 .
. ,
, .
.


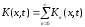
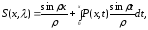



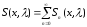 ,
,



