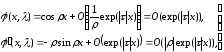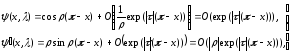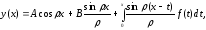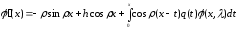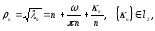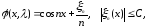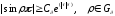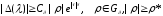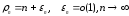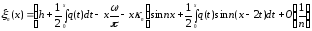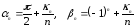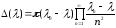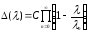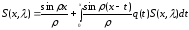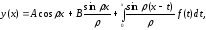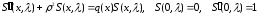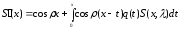СОДЕРЖАНИЕ
|
Введение…………………………………. |
.…………………………………………...3 |
|
….………………………………………...5 |
|
…………………………………………..17 |
|
….……………………………………….23 |
|
….……………………………………….31 |
|
Список использованных источников…. |
….……………………………………….36 |
ВВЕДЕНИЕ
Обратные задачи спектрального анализа состоят в восстановлении дифференциальных операторов по их спектральным характеристикам. Подобные задачи играют важную роль не только в различных разделах математики, но и имеют много приложений в естествознании и технике.
Наиболее полные результаты в теории обратных спектральных задач получены для дифференциального оператора Штурма-Лиувилля
|
|
(1) |
Первые исследования по спектральной теории операторов вида (1) были выполнены в связи с уравнением, описывающим колебание струны в XIX веке, а интенсивное развитие данная теория для различных классов операторов получила век спустя. Что касается обратных спектральных задач, то основные результаты и методы здесь были получены во второй половине XX века. Созданные методы позволили решить целый ряд важных прикладных задач в механике, физике, электронике, геофизике, метеорологии и других областях естествознания и техники. Интерес к этой тематике постоянно увеличивается благодаря появлению все новых приложений, и в настоящее время интенсивно развивается теория обратных задач во всем мире.
Целью данной курсовой работы является описание метода Гельфанда-Левитана. Метод позволяет получить алгоритм решения обратной задачи для дифференциального оператора Штурма-Лиувилля, определяемого уравнением

и краевыми условиями
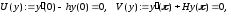
где λ – спектральный параметр; q(x),
h и H
вещественны;
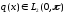 .
.
Курсовая работа состоит из введения,
четырех глав и списка использованных
источников. В первой главе изучаются
основные спектральные характеристики
краевых задач Штурма-Лиувилля на конечном
интервале. В частности, доказана теорема
о существовании и асимптотическом
поведении собственных значений и
собственных функций. Во второй главе
исследуются свойства собственных
функций. Доказано, что система собственных
функций является полной и образует
ортогональный базис в пространстве
 .
В третьей главе строятся операторы
преобразования, которые являются
эффективным инструментом в спектральной
теории операторов Штурма-Лиувилля. В
четвертой главе приведен алгоритм
решения обратной задачи методом Гельфанда
– Левитана, который позволяет свести
данную задачу к линейному интегральному
уравнению.
.
В третьей главе строятся операторы
преобразования, которые являются
эффективным инструментом в спектральной
теории операторов Штурма-Лиувилля. В
четвертой главе приведен алгоритм
решения обратной задачи методом Гельфанда
– Левитана, который позволяет свести
данную задачу к линейному интегральному
уравнению.
-
Поведение спектра
Рассмотрим краевую задачу L=L(q(x), h, H):
|
|
(1.1) |
|
(1.2) |
Здесь λ – спектральный параметр; q(x),
h и H
вещественны;
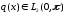 .
Оператор
.
Оператор
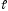 называется оператором Штурма-Лиувилля,
а функцию q мы в
дальнейшем будем называть потенциалом.
называется оператором Штурма-Лиувилля,
а функцию q мы в
дальнейшем будем называть потенциалом.
Нас интересуют нетривиальные решения краевой задачи (1.1)-(1.2)
Определение 1.1. Те значения параметра λ, для которых L имеет нетривиальные решения называются собственными значениями, а соответствующие нетривиальные решения называются собственными функциями. Множество собственных значений называется спектром L.
В этом разделе мы получим свойства спектра краевой задачи L и изучим асимптотическое поведение собственных значений и собственных функций.
Пусть
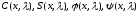 являются решениями уравнения (1.1) при
начальных условиях
являются решениями уравнения (1.1) при
начальных условиях
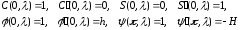
При каждом фиксированном x
функции
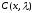 ,
,
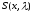 ,
,
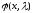 ,
,
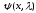 являются целыми аналитическими функциями
по λ. Ясно, что
являются целыми аналитическими функциями
по λ. Ясно, что
|
|
(1.3) |
Обозначим
|
|
(1.4) |
где
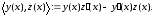
Согласно формуле Остроградского-Лиувилля,
вронскиан
 не зависит от x. Функция
не зависит от x. Функция
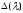 называется характеристической функцией
краевой задачи L.
Подставляя
называется характеристической функцией
краевой задачи L.
Подставляя
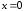 и
и
 в (1.4)
в (1.4)
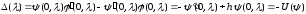
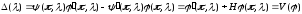
получаем
|
|
(1.5) |
Функция
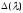 является целой по λ и имеет не более
счетного множества нулей
является целой по λ и имеет не более
счетного множества нулей
 .
.
Теорема 1.1. Нули
 характеристической функции совпадают
с собственными значениями краевой
задачи L. Функции
характеристической функции совпадают
с собственными значениями краевой
задачи L. Функции
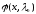 и
и
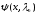 являются собственными функциями, и
существует последовательность
являются собственными функциями, и
существует последовательность
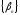 такая, что
такая, что
|
|
(1.6) |
Доказательство:
-
Пусть
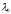 является нулем функции
является нулем функции
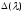 .
Тогда, в силу (1.3)-(1.5)
.
Тогда, в силу (1.3)-(1.5)
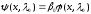 ,
и функции
,
и функции
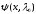 ,
,
 удовлетворяют краевым условиям (1.2).
Следовательно,
удовлетворяют краевым условиям (1.2).
Следовательно,
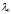 - собственное значение, а
- собственное значение, а
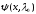 ,
,
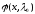 - соответствующие собственные функции.
- соответствующие собственные функции. -
Обратно, пусть
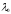 является собственным значением L,
и пусть
является собственным значением L,
и пусть
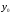 - соответствующая собственная функция.
Тогда
- соответствующая собственная функция.
Тогда
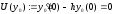
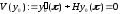
Ясно,
что
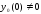 (если бы
(если бы
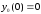 ,
то
,
то
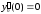 ,
и по теореме единственности решения
задачи Коши
,
и по теореме единственности решения
задачи Коши
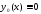 ).
Без ограничения общности полагаем
).
Без ограничения общности полагаем
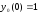 .
Тогда
.
Тогда
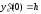 ,
и следовательно
,
и следовательно
 .
Поэтому (1.5) дает
.
Поэтому (1.5) дает
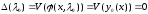 .
Мы также доказали, что каждому собственному
значению соответствует только одна (с
точностью до постоянного множителя)
собственная функция. □
.
Мы также доказали, что каждому собственному
значению соответствует только одна (с
точностью до постоянного множителя)
собственная функция. □
Обозначим
|
|
(1.7) |
Числа
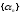 называются весовыми числами, а числа
называются весовыми числами, а числа
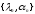 называются спектральными данными
краевой задачи L.
называются спектральными данными
краевой задачи L.
Лемма 1.1. Справедливо соотношение
|
|
(1.8) |
где числа
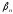 определяются формулой (1.6) и
определяются формулой (1.6) и
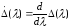 .
.
Доказательство:
Так как
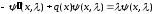 ,
,
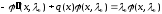 ,
,
то
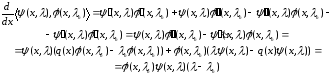
и, следовательно, с учетом (1.5) имеем
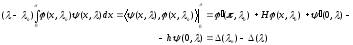
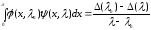
При
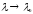 получаем
получаем
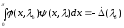
используя (1.6) и (1.7) получаем,
|
|
□ |
Теорема 1.2. Собственные значения
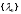 и собственные функции
и собственные функции
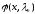 ,
,
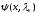 - вещественны. Все нули
- вещественны. Все нули
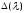 являются простыми, то есть
являются простыми, то есть
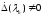 .
Собственные функции соответствующие
различным собственным значениям
ортогональны в
.
Собственные функции соответствующие
различным собственным значениям
ортогональны в
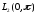 .
.
Доказательство:
Пусть
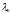 и
и
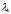
 - собственные значения с собственными
функциями
- собственные значения с собственными
функциями
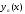 и
и
 соответственно. Вычисляем
соответственно. Вычисляем
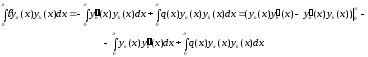
так как
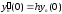 ,
,
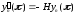 ,
то подстановка исчезает. Поэтому
,
то подстановка исчезает. Поэтому
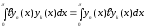 .
.
Так как
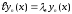 ,
то
,
то
 и так как
и так как
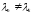 ,
то имеем
,
то имеем
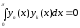 .
.
Далее, пусть
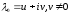 - невещественное собственное значение
с собственной функцией
- невещественное собственное значение
с собственной функцией
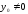 .
Тогда
.
Тогда
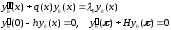
Так как
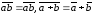 и
и
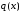 ,
,
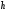 и
и
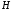 вещественны, то
вещественны, то
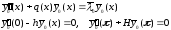
то есть
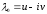 - также собственное значение с собственной
функцией
- также собственное значение с собственной
функцией
 .
Так как
.
Так как
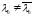 ,
то
,
то
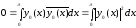
что невозможно. Таким образом, все
собственные значения
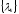 задачи L вещественны.
И, следовательно, собственные функции
задачи L вещественны.
И, следовательно, собственные функции
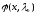 ,
,
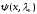 также вещественны, так как
также вещественны, так как
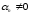 ,
,
 ,
то в силу (1.8) имеем
,
то в силу (1.8) имеем
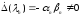 .
□
.
□
Пример 1.1. Пусть
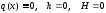 ,
и пусть
,
и пусть
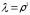 .
Тогда (1.1) - (1.2) примет вид:
.
Тогда (1.1) - (1.2) примет вид:
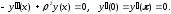
Общее решение этого уравнения имеет вид:
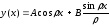
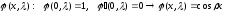
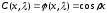
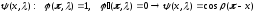
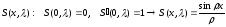
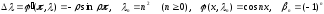
Замечание 1.1. Пусть здесь и в дальнейшем
 ,
,
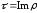 .
Покажем, что
.
Покажем, что
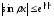 ,
,
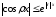 .
.
В самом деле, пусть
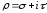 .
Тогда
.
Тогда
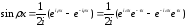 .
.
Так как
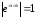 ,
то
,
то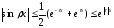 .
.
Аналогично для
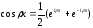
Лемма 1.2. При
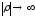 верны следующие асимптотические оценки:
верны следующие асимптотические оценки:
|
|
(1.9)
(1.10) |
равномерно по
 .
.
 и
и
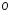 символы Ландау.
символы Ландау.
Доказательство:
Рассмотрим уравнение
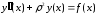
Метод вариаций произвольных постоянных дает
|
|
(*) |
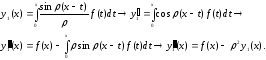
Из (*) следует
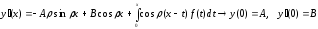
Функция
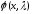 является решением задачи Коши
является решением задачи Коши
|
|
(**) |
Применим (*). У нас
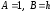 .
Тогда
.
Тогда
|
|
(1.11) |
Пусть верно (1.11). Тогда
|
|
(1.12) |
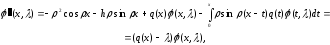
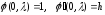
и следовательно, верно (**).
Вспомним:
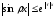 ,
,
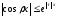 .
Умножим (1.11) на
.
Умножим (1.11) на
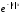 :
:

Обозначим
 .
.
При
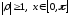 имеем
имеем
 ,
,
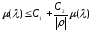 или
или
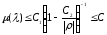
при достаточно больших
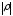 .
.
Поэтому
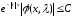 или
или
 .
.
Подставляя эту оценку в правую часть (1.11) и (1.12) получаем
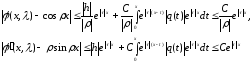
и приходим к (1.9).
Аналогично получается и (1.10). Заметим, что (1.10) может быть получено, используя (1.9). В самом деле,
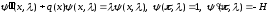 .
.
Рассмотрим функцию
 Тогда
Тогда
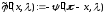 ,
,
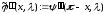 .
Следовательно,
.
Следовательно,
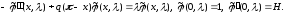
Поэтому (1.9) верно и для
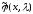 .
Так как
.
Так как
 ,
то получаем (1.10).
□
,
то получаем (1.10).
□
Теорема 1.3. Краевая задача
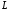 имеет
счетное множество собственных значений
имеет
счетное множество собственных значений
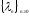 .
При этом
.
При этом
|
|
(1.13) |
|
|
(1.14) |
где
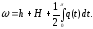
Здесь и в дальнейшем один и тот же символ
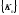 обозначает различные последовательности
из
обозначает различные последовательности
из
 ,
а символ
,
а символ
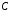 обозначает различные положительные
константы, не зависящие от
обозначает различные положительные
константы, не зависящие от
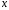 ,
,
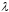 и
и
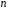 .
.
Доказательство:
-
Подставляя асимптотику для
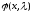 из (1.9) в правые части (1.11) и (1.12), вычисляем
из (1.9) в правые части (1.11) и (1.12), вычисляем
|
|
(1.15) |
где
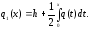
Согласно, (1.5) ,
 .
Следовательно, в силу (1.15), имеем
.
Следовательно, в силу (1.15), имеем
|
|
(1.16) |
где
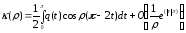 .
.
-
Обозначим
 ,
,
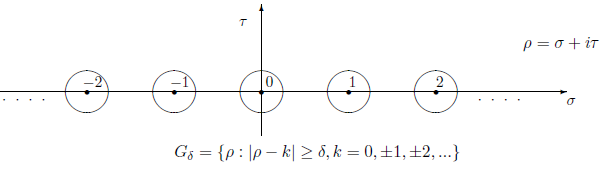
покажем, что
|
|
(1.17) |
|
|
(1.18) |
при достаточно большом
 .
.
Пусть
 .
Достаточно доказать (1.17) для области
.
Достаточно доказать (1.17) для области
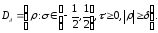
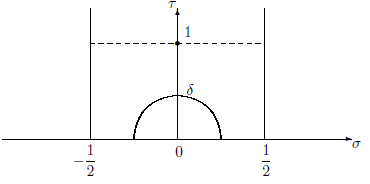
Положим
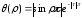 .
Пусть
.
Пусть
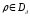 .
При
.
При
 имеем
имеем
 .
Так как
.
Так как
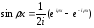 ,
то при
,
то при
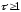
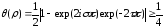 ,
(так как
,
(так как
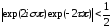 )
)
Таким образом (1.17) доказано. Далее,
используя (1.16), получаем для
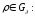
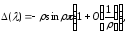
и, следовательно, (1.18) доказано.
-
Обозначим
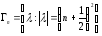 .
.
В силу (1.16)
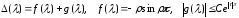 .
.
Согласно (1.17),
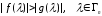 при достаточно больших
при достаточно больших
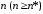 .
Тогда по теореме Руше число нулей функции
.
Тогда по теореме Руше число нулей функции
 внутри
внутри
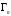 совпадает с числом нулей функции
совпадает с числом нулей функции
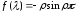 ,
то есть равно
,
то есть равно
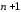 .
Таким образом, в круге
.
Таким образом, в круге
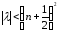 расположено
расположено
 собственных значений краевой задачи
собственных значений краевой задачи
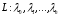 .
Применяя теперь теорему Руше к кругу
.
Применяя теперь теорему Руше к кругу
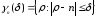 ,
заключаем, что при достаточно больших
,
заключаем, что при достаточно больших
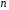 в
в
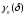 лежит ровно один ноль функции
лежит ровно один ноль функции
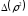 ,
а именно
,
а именно
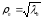 .
В силу произвольности
.
В силу произвольности
 имеем
имеем
|
|
(1.19) |
Подставляя (1.19) в (1.16), получаем
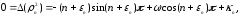
и, следовательно
|
|
(1.20) |
Тогда
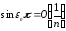 ,
то есть
,
то есть
 .
С помощью (1.20), вычисляем более точно
.
С помощью (1.20), вычисляем более точно
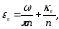 то есть (1.13) доказано. Подставляя (1.13) в
(1.15), приходим к (1.14), где
то есть (1.13) доказано. Подставляя (1.13) в
(1.15), приходим к (1.14), где
|
|
(1.21) |
Следовательно,
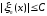 ,
и теорема 1.3 доказана. □
,
и теорема 1.3 доказана. □
В силу (1.6) при
 имеем
имеем
 .
.
Тогда, используя (1.7), (1.14), (1.21), получаем
|
|
|
Через
 обозначим пространство функций
обозначим пространство функций
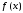 ,
,
 таких, что функции
таких, что функции
 абсолютно непрерывны и
абсолютно непрерывны и
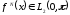 .
.
Теорема 1.4. Задание спектра
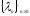 однозначно определяет характеристическую
функцию
однозначно определяет характеристическую
функцию
 по формуле
по формуле
|
|
(1.22) |
Доказательство:
Из (1.16) вытекает, что
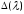 является целой по
является целой по
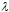 функцией порядка ½ и, следовательно, по
теореме Адамара
функцией порядка ½ и, следовательно, по
теореме Адамара
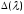 однозначно определяется своими нулями
с точностью до постоянного множителя:
однозначно определяется своими нулями
с точностью до постоянного множителя:
|
|
(1.23) |
Рассмотрим функцию
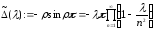 .
.
Тогда
 .
.
Учитывая (1.13) и (1.16), вычисляем

и, следовательно,
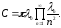
Подставляя это в (1.23), приходим к (1.22). □
Теорема 1.5. Функция
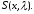 удовлетворяет следующему интегральному
уравнению:
удовлетворяет следующему интегральному
уравнению:
|
|
(1.24) |
Доказательство:
Рассмотрим уравнение
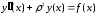
Метод вариаций произвольных постоянных дает
|
|
(*) |
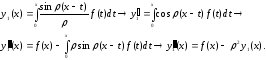
Из (*) следует
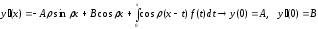
Функция
 является решением задачи Коши
является решением задачи Коши
|
|
(**) |
Применим (*). У нас
 .
Тогда
.
Тогда
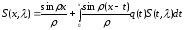
Пусть верно (1.24). Тогда
|
|
|
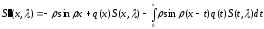
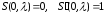 и, следовательно, верно (**).
□
и, следовательно, верно (**).
□

 .
.
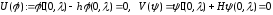
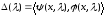 ,
,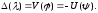
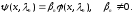
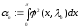 .
. ,
,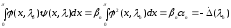 .
.