
- •Содержание
- •Глава I. Основные понятия
- •1.1 Понятие линейного пространства
- •1.2 Определение линейного подпространства
- •Глава II. Способы описания подпространств линейного пространства
- •2.1 Линейное подпространство задано однородной системой линейных уравнений
- •2.2 Линейное подпространство задано линейной оболочкой
- •Глава III . Сумма и пересечение подпространств
- •Глава IV. Примеры Пример 1.
- •Пример 2
- •Пример 3
- •Пример 4
- •Глава V. Практическая часть Задача 1
- •Решение:
- •Задача 2
- •Решение:
- •Задача 3
- •Решение:
- •Задача 4
- •Решение:
- •Заключение
- •Список использованной литературы
- •«Воронежский государственный педагогический университет»
Решение:
Обозначим
через
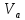 подмножество всех верхних треугольных
матриц. Это подмножество не пусто, так
как содержит, например,нулевую матрицу
порядка
подмножество всех верхних треугольных
матриц. Это подмножество не пусто, так
как содержит, например,нулевую матрицу
порядка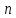 .
Пусть
.
Пусть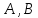 — произвольные верхние треугольные
матрицы порядка
— произвольные верхние треугольные
матрицы порядка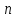 .
Это значит, что их элементы
.
Это значит, что их элементы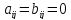 для
для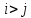 .
Тогда все элементы матрицы
.
Тогда все элементы матрицы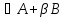 с
с
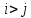 равны нулю
для
любых
равны нулю
для
любых
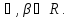 Значит,
Значит,
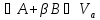 .
Мы получили, что подмножество всех
верхних треугольных матриц является
подпространством линейного пространства
.
Мы получили, что подмножество всех
верхних треугольных матриц является
подпространством линейного пространства
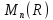 .
Аналогично, нетрудно показать, что
подмножество всех нижних треугольных
матриц является подпространством
линейного пространства
.
Аналогично, нетрудно показать, что
подмножество всех нижних треугольных
матриц является подпространством
линейного пространства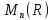 .
.
Задача 2
Для
каждого из следующих множеств
геометрических векторов определить,
будет ли это множество линейным
подпространством пространства
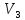 :13
:13
1) радиус-векторы точек данной плоскости;
2)
векторы, образующие с данным ненулевым
вектором
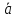 угол
угол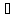 ;
;
3)
множество векторов, удовлетворяющих
условию
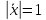 .
.
Решение:
По
определению подмножество
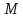 элементов линейного пространства
элементов линейного пространства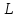 называется подпространством пространства
называется подпространством пространства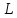 ,
если выполнены два условия:
,
если выполнены два условия:
1)
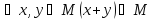
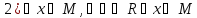
Проверим выполнение этих условий в каждом случае:
1.
Множество радиус-векторов точек плоскости
(то есть векторов с началом в начале
координат и концом в искомой точке)
является линейным подпространством
пространства
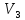 ,
так как выполнены оба условия определения.
,
так как выполнены оба условия определения.
Действительно, сумма двух векторов с началом в начале координат есть вектор с началом в начале координат, то есть радиус-вектор некоторой точки (правило параллелограмма сложения векторов, см. рисунок 1). Произведение вектора на число дает вектор с началом в той же точке, но растянутый/сжатый в некоторое число раз, то есть тоже радиус-вектор некоторой точки.
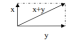
Рис. 1.
2.
Множество векторов, образующих с данным
ненулевым вектором
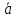 угол α не является линейным подпространством
пространства
угол α не является линейным подпространством
пространства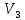 ,
так как невыполнено первое условие
определения. Действительно, можно найти
такие два вектора
,
так как невыполнено первое условие
определения. Действительно, можно найти
такие два вектора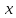 и
и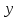 ,
образующие с данным ненулевым вектором
,
образующие с данным ненулевым вектором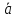 угол α, что их сумма
угол α, что их сумма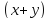 не будет образовывать с вектором
не будет образовывать с вектором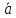 угол α (см. рисунок 2).
угол α (см. рисунок 2).
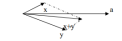
Рис. 2
3.
Множество векторов, удовлетворяющих
условию
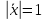 не
является линейным подпространством
пространства
не
является линейным подпространством
пространства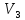 ,
так как не выполнено второе условие
определения. Действительно, если умножить
любой вектор, такой что
,
так как не выполнено второе условие
определения. Действительно, если умножить
любой вектор, такой что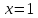 на любое число
на любое число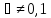 ,
то получим новый вектор, длина которого
,
то получим новый вектор, длина которого
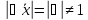 .
.
Задача 3
Найдите
ранг и базис набора векторов
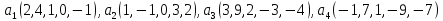 .14
.14
Решение:
Выпишем матрицу и решим её методом Жордана-Гаусса:

Видим,
что
 (строчек
две ).Так как дана линейная оболочка, то
:
(строчек
две ).Так как дана линейная оболочка, то
:
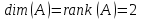
Итак,
в базисе 2 вектора, так как dim(A)
= 2. Мы должны выбрать 2 линейно-независимых
вектора, которые входят в данное линейное
подпространство. Для двух векторов
линейная зависимость означает
пропорциональность. Значит, выберем 2
непропорциональных вектора. Это,
например,
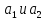 .
.
Выпишем фундаментальный набор решений:
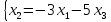
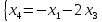
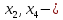 базисные
переменные
базисные
переменные
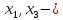 свободные
переменные
свободные
переменные
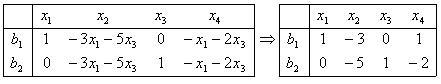
Получили
базис:
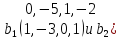 )
)
Ответ:
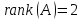 ;
;
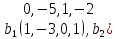 )
) базис.
базис.
Задача 4
Пусть
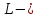 множество
многочленов степени не выше
множество
многочленов степени не выше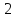 ,
удовлетворяющих условию
,
удовлетворяющих условию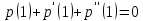 .
Доказать, что
.
Доказать, что
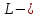 линейное
подпространство в пространстве
линейное
подпространство в пространстве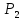 .
Найти его базис и размерность. Дополнить
базис подпространства до базиса всего
пространства.15
.
Найти его базис и размерность. Дополнить
базис подпространства до базиса всего
пространства.15
