Содержание

Введение…………………………………………………………...........................3

Глава I. Основные понятия……………………………………………………….5

1.1 Понятие линейного пространства……………………..…………………..5

1.2 Определение линейного подпространства…………………………….….7

Глава II. Способы описания подпространств линейного пространства……….8

2. 1. Линейное подпространство задано однородной системой линейных уравнений………………………………………………………………………….8

2. 2. Линейное подпространство задано линейной оболочкой……………..9

Глава III . Сумма и пересечение подпространств.…………………………….10

Глава IV. Примеры………………………………………………………………15

Глава V. Практическая часть……………………………………………………18

Заключение……………………………………………………………………….24

Список использованной литературы…………………………………………...25

Введение

Линейная алгебра – важная в приложениях часть алгебры, изучающая векторы, векторные, или линейные пространства, линейные отображения и системы линейных уравнений. Векторные пространства встречаются в математике и её приложениях повсеместно. Линейная алгебра широко используется в абстрактной алгебре и функциональном анализе и находит многочисленные приложения в естественных науках.

Предметом изучения линейной алгебры служат именно конечномерные линейные пространства. Бесконечномерные линейные пространства также важны и широко используются, например, в современной физике.

На сегодняшний день моя тема актуальна, потому что мы часто встречаемся в линейной алгебре с линейными подпространствами. Знать, что представляет подпространство, знать критерии подпространства, я думаю, должен каждый.

Все вышесказанное и обусловило выбор темы курсовой работы: «Подпространства. Критерии подпространства. Примеры».

Цель курсовой работы – изучить линейное подпространство, его критерии, рассмотреть различные примеры подпространств.

Объектом исследования в данной работе является линейное подпространство, его критерии, рассмотрение различных примеров подпространств.

В соответствии с поставленной целью в работе должны быть решены следующие задачи:

1) изучить основные понятия линейного пространства;

2)рассмотреть и изучить основные способы описания подпространств линейного пространства;

3) изучить сумму и пересечение подпространств;

4) изучить и проанализировать примеры линейного подпространства.

При выполнении работы используется монографический метод исследования, математический метод (метод визуализации данных (функции, графики).

Теоретическую и методическую основы курсовой работы составляют труды отечественных ученых по данному вопросу.

Глава I. Основные понятия

1.1 Понятие линейного пространства

Вспомним одну из важных задач математического анализа: по заданной функции найти ее первообразную, т. е. такую функцию, чтоОбщее решение этой задачи, как известно, таково: если существует хоть одна первообразная, то любая из них может быть получена по формул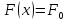е(x)+C, где - произвольная постоянная. Заметим, что постоянная - решение однородного сходна с общим решением системы линейных уравнений: общее решение есть сумма одного из решений и общего решения однородного уравнения. ¹

Сходство здесь, конечно, не случайное. Оно следует из совпадения алгебраических свойств операций дифференцирования и матричного умножения по отношению к линейным операциям.

Естественно возникает необходимость исследовать множество, состоящее из элементов какой угодно природы, в котором определены операции сложения двух элементов и умножения элемента на число.

Эти операции могут быть определены любым образом, лишь бы они обладали определенным набором свойств.

Определение: множество называется линейным пространством, а его элементы - векторами, если:

• задан закон «операция сложения», по которому любым двум элементам иизсопоставляется элемент из, называемый их суммой и обозначаемый;

• задан закон «операция умножения на число» , по которому элементу изи числу ⍺ сопоставляется элемент из, называемый произведениемна ⍺ и обозначаемый;

• для любых элементов ,иизи любых чисел ⍺ и β выполнены следующие требования (или аксиомы):

1. ;

2. ;

3. существует элемент такой, что для каждого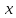извыполне

но ;

4) для любого существует элементтакой, что;

5) ;

6)

7) ;

8) произведение на числоравно, т.е.

Если мы ограничиваемся вещественными числами, то 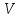называется

вещественным линейным пространством, если же определено умножение на любое комплексное число, то линейное пространство называется комплексным.²

Вектор называется противоположным вектору, векторназывается нулевым вектором или нулем.