
- •8. Системы координат на плоскости: декартовы и полярные координаты
- •17. Кривые второго порядка
- •1. Окружность
- •2. Эллипс
- •3. Гипербола
- •4. Парабола
- •1. Основные формулы в декартовых прямоугольных координатах
- •Непрерывность ф-ции, имеющей производную.
- •37.Общая схема исследования функции и построения её графика
- •40. 40. Непосредственное интегрирование.
- •41. Интегрирование методом подстановки.
- •Интегрирование по частям.
- •47.Существование и единственность решения
- •Таким образом, .
- •Дифференциальные уравнения с разделенными переменными .
7. Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.
Пусть
дана система линейных уравнений с
![]() неизвестными
(над произвольным полем):
неизвестными
(над произвольным полем):

Тогда её можно переписать в матричной форме:
![]() ,
где
,
где
![]() —
основная матрица системы,
—
основная матрица системы,![]() и
и![]() —
столбцы свободных членов и решений
системы соответственно:
—
столбцы свободных членов и решений
системы соответственно:

Умножим
это матричное уравнение слева на
![]() —
матрицу, обратную к матрице
—
матрицу, обратную к матрице![]() :
:![]()
Так
как
![]() ,
получаем
,
получаем![]() .
Правая часть этого уравнения даст
столбец решений исходной системы.
Условием применимости данного метода
(как и вообще существования решения
неоднородной системы линейных уравнений
с числом уравнений, равным числу
неизвестных) являетсяневырожденность
матрицы A. Необходимым и достаточным
условием этого является неравенство
нулю определителя
матрицы
A:
.
Правая часть этого уравнения даст
столбец решений исходной системы.
Условием применимости данного метода
(как и вообще существования решения
неоднородной системы линейных уравнений
с числом уравнений, равным числу
неизвестных) являетсяневырожденность
матрицы A. Необходимым и достаточным
условием этого является неравенство
нулю определителя
матрицы
A:
![]() .
.
Для
однородной системы линейных уравнений,
то есть когда вектор
![]() ,
действительно обратное правило: система
,
действительно обратное правило: система![]() имеет
нетривиальное (то есть ненулевое) решение
только если
имеет
нетривиальное (то есть ненулевое) решение
только если![]() .
Такая связь между решениями однородных
и неоднородных систем линейных уравнений
носит названиеальтернативы
Фредгольма.
.
Такая связь между решениями однородных
и неоднородных систем линейных уравнений
носит названиеальтернативы
Фредгольма.
Пример решения неоднородной СЛАУ[править | править вики-текст]

Сначала убедимся в том, что определитель матрицы из коэффициентов при неизвестных СЛАУ не равен нулю.

Теперь вычислим алгебраические дополнения для элементов матрицы, состоящей из коэффициентов при неизвестных. Они нам понадобятся для нахождения обратной матрицы.

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Далее найдём союзную матрицу, транспонируем её и подставим в формулу для нахождения обратной матрицы.
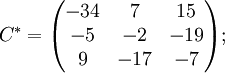
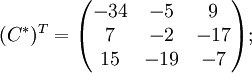
![]()
Подставляя переменные в формулу, получаем:

Осталось найти неизвестные. Для этого перемножим обратную матрицу и столбец свободных членов.
![]()
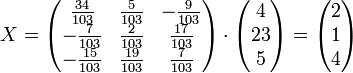
Итак, x=2; y=1; z=4.
8. Системы координат на плоскости: декартовы и полярные координаты
Декартова система координат на плоскости определяется некоторой ее точкой O и базисом из двух векторов, параллельных плоскости. Точка O называется началом координат. Прямые, проведенные через начало координат в направлении базисных векторов, называются осями координат. Они лежат в плоскости и называются осями абсцисс и ординат. Каждая ось координат является числовой осью с началом в точке O, положительным направлением, совпадающим с направлением соответствующего базисного вектора, и единицей длины, равной длине этого вектора.
Координатами точки M называются координаты вектора OM (радиус–вектора) (см. рис. 1).

Если базис ортонормированный, то связанная с ним декартова система координат называется прямоугольной.
На плоскости часто употребляется также полярная система координат (рис. 2).

Она определяется точкой O, называемой полюсом, и лучом, исходящим из полюса, называемым полярной осью. Полярными координатами ρ и точки M называются расстояние ρ от полюса до точки M ( ρ = |OM|) и угол между полярной осью и вектором OM (рис. 2). Угол называется полярным углом, измеряется в радианах и отсчитывается от полярной оси против часовой стрелки. Полярные координаты точки O: ρ = 0, угол не определен. У остальных точек ρ > 0 и угол определен с точностью до 2π. Обычно полагают 0 ≤ < 2 π или − π < ≤ π.
Если полюс совпадает с началом прямоугольной декартовой системы координат, а полярная ось — с положительной частью оси абсцисс, то декартовы координаты x и y точки M выражаются через ее полярные координаты ρ и формулами
x = ρcos y = ρsin .
Полярные координаты ρ и точки M выражаются через ее декартовы координаты x и y формулами
|
ρ |
= |
√ |
|
|
cos =
|
|
sin =
|
Замечание. Если не указано положение полюса и полярной оси относительно декартовой системы координат, то считаем, что полюс совпадает с началом прямоугольной декартовой системы координат, а полярная ось — с положительной частью оси абсцисс.
14. Уравнения прямой на плоскости
Простейшей из линий является прямая. Разным способам задания прямой соответствуют в прямоугольной системе координат разные виды её уравнений.
Уравнение прямой с угловым коэффициентом
Пусть на плоскости Оху задана произвольная прямая, не параллельная оси Оу. Ее положение вполне определяется ординатой b точки N(0; b) пересечения с осью Оу и углом a между осью Ох и прямой (см. рис. 41).
Под углом а (0<a< )
наклона прямой понимается наименьший
угол, на который нужно повернуть вокруг
точки пересечения прямой и оси Ох против
часовой стрелки ось Ох до ее совпадения
с прямой. Возьмем на прямой произвольную
точку М(х;у) (см. рис. 41). Проведем через
точку N ось Nx', параллельную оси Ох и
одинаково с ней направленную. Угол между
осью Nx' и прямой равен a. В системе Nx'y
точка Μ имеет координаты x и у-b.
Из определения тангенса угла следует равенство
![]() ,
т. е.
,
т. е.![]() .
.
Введем обозначение tga=k, получаем уравнение
![]() (10.2)
(10.2)
которому удовлетворяют координаты любой точки М(х;у) прямой. Можно убедиться, что координаты любой точки Р(х;у), лежащей вне данной прямой, уравнению (10.2) не удовлетворяют.
Число k = tga называется угловым коэффициентом прямой, а уравнение (10.2) — уравнением прямой с угловым коэффициентом.
Если прямая проходит через начало координат, то b = 0 и, следовательно, уравнение этой прямой будет иметь вид y=kx.
Если прямая параллельна оси Ох, то a = 0, следовательно, k = tga = 0 и уравнение (10.2) примет вид у = b.
Если прямая параллельна оси Оу, то
![]() ,
уравнение (10.2) теряет смысл, т. к. для нее
угловой коэффициент
,
уравнение (10.2) теряет смысл, т. к. для нее
угловой коэффициент![]() не
существует.
не
существует.
В этом случае уравнение прямой будет иметь вид
![]() (10.3)
(10.3)
где a— абсцисса точки пересечения прямой с осью Ох. Отметим, что уравнения (10.2) и (10.3) есть уравнения первой степени.
Общее уравнение прямой.
Рассмотрим уравнение первой степени относительно x и y в общем виде
![]() (10.4)
(10.4)
где А, В, С — произвольные числа, причем А и В не равны нулю одновременно.
Покажем, что уравнение (10.4) есть уравнение прямой линии. Возможны два случая.
Если В = 0, то уравнение (10.4) имеет
вид Ах + С = О, причем А ¹ 0 т. е.
![]() .
Это есть уравнение прямой, параллельной
оси Оу и проходящей через точку
.
Это есть уравнение прямой, параллельной
оси Оу и проходящей через точку![]() ·
·
Если B ¹ 0, то из уравнения (10.4) получаем
![]() .
Это есть уравнение прямой с угловым
коэффициентом
.
Это есть уравнение прямой с угловым
коэффициентом![]() |.
|.
Итак, уравнение (10.4) есть уравнение прямой линии, оно называется общим уравнением прямой.
Некоторые частные случаи общего уравнения прямой:
1) если А = 0, то уравнение приводится
к виду![]() .
Это есть уравнение прямой, параллельной
оси Ох;
.
Это есть уравнение прямой, параллельной
оси Ох;
2) если В = 0, то прямая параллельна оси Оу;
3) если С = 0, то получаем
![]() .
Уравнению удовлетворяют координаты
точки O(0;0), прямая проходит через начало
координат.
.
Уравнению удовлетворяют координаты
точки O(0;0), прямая проходит через начало
координат.
Уравнение прямой, проходящей через данную точку в данном направлении
Пусть прямая проходит через точку
![]() и
ее направление определяется угловым
коэффициентом k. Уравнение этой прямой
можно записать в виде
и
ее направление определяется угловым
коэффициентом k. Уравнение этой прямой
можно записать в виде![]() ,
где b — пока неизвестная величина. Так
как прямая проходит через точку
,
где b — пока неизвестная величина. Так
как прямая проходит через точку![]() ,
то координаты точки удовлетворяют
уравнению прямой:
,
то координаты точки удовлетворяют
уравнению прямой:![]() .
Отсюда
.
Отсюда![]() .
Подставляя значение b в уравнение
.
Подставляя значение b в уравнение![]() ,
получим искомое уравнение прямой:
,
получим искомое уравнение прямой:![]() ,
т. е.
,
т. е.
![]() (10.5)
(10.5)
Уравнение (10.5) с различными значениями
k называют также уравнениями пучка
прямых с центром в точке![]() Из
этого пучка нельзя определить лишь
прямую, параллельную оси Оу.
Из
этого пучка нельзя определить лишь
прямую, параллельную оси Оу.
Уравнение прямой, проходящей через две точки
Пусть прямая проходит через точки
![]() и
и![]() .
Уравнения прямой, проходящей через
точку M1, имеет вид
.
Уравнения прямой, проходящей через
точку M1, имеет вид
![]()
![]() (10.6)
(10.6)
где k — пока неизвестный коэффициент.
Так как прямая проходит через точку
![]() ,
то координаты этой точки должны
удовлетворять уравнению (10.6):
,
то координаты этой точки должны
удовлетворять уравнению (10.6):![]() .
Οтсюда находим
.
Οтсюда находим![]() .
Подставляя найденное значение k в
уравнение (10.6), получим уравнение
прямой, проходящей через точкиM1
и M2.
.
Подставляя найденное значение k в
уравнение (10.6), получим уравнение
прямой, проходящей через точкиM1
и M2.
 (10.7)
(10.7)
Предполагается, что в этом уравнении
![]() ·
·
Если x2= x1прямая, проходящая
через точки![]() и
и![]() параллельна
оси ординат. Ее уравнение имеет вид
параллельна
оси ординат. Ее уравнение имеет вид![]() .
.
Если y2 = y1то уравнение
прямой может быть записано в виде![]() ,
прямаяM1M2параллельна оси абсцисс.
,
прямаяM1M2параллельна оси абсцисс.
Уравнение прямой в отрезках
Пусть прямая пересекает ось Ох в точке
![]() ,
а ось Оу – в точке
,
а ось Оу – в точке![]() (см.
рис. 42). В этом случае уравнение (10.7)
примет вид
(см.
рис. 42). В этом случае уравнение (10.7)
примет вид
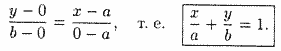
Это уравнение называется уравнением прямой в отрезках, так как числа α и b указывают, какие отрезки отсекает прямая на осях координат.
Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
Найдем уравнение прямой,
проходящей через заданную
точку
![]() перпендикулярно
данному ненулевому вектору
перпендикулярно
данному ненулевому вектору![]() .
.
Возьмем на прямой произвольную точку
М(х;у) и рассмотрим вектор
![]() (см.
рис. 43). Поскольку векторы
(см.
рис. 43). Поскольку векторы![]() и
и![]() перпендикулярны,
то их скалярное произведение равно
нулю:
перпендикулярны,
то их скалярное произведение равно
нулю:![]() ,
то есть
,
то есть
![]()
Уравнение (10.8) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору.
Вектор
![]() ,
перпендикулярный прямой, называется
нормальным вектором этой прямой.
Уравнение (10.8) можно переписать в виде
,
перпендикулярный прямой, называется
нормальным вектором этой прямой.
Уравнение (10.8) можно переписать в виде
![]() (10.9)
(10.9)
где А и B— координаты нормального
вектора,
![]() —
свободный член. Уравнение (10.9) есть
общее уравнение прямой (см. (10.4)).
—
свободный член. Уравнение (10.9) есть
общее уравнение прямой (см. (10.4)).
