
- •Практикум 2.3. Числовые ряды Краткие теоретические сведения и практические упражнения
- •Числовой ряд. Сходящиеся и расходящиеся ряды. Сумма ряда.
- •Необходимый признак сходимости.
- •Общие свойства рядов.
- •Признаки сходимости рядов с положительными членами
- •Оценка остатка ряда с положительными членами
- •Знакочередующиеся ряды
- •Задания для самостоятельной работы
- •Список рекомендуемой литературы
Общие свойства рядов.
|
1) Если ряд
2) Если ряды
3)
Если ряд
|
Практически в каждом учебнике по математическому анализу можно найти доказательства этих свойств (впрочем, Вы можете доказать их и самостоятельно, опираясь на свойства числовых рядов).
А что получится, если складывать расходящиеся ряды?
Упражнение 4.
а) Пусть ряд
![]() сходится,
сходится,![]() расходится. Что можно сказать о сходимости
ряда
расходится. Что можно сказать о сходимости
ряда![]() ?
Проиллюстрируйте Ваше предположение
на примере, используя М-файл из упр. 1.
?
Проиллюстрируйте Ваше предположение
на примере, используя М-файл из упр. 1.
б) Пусть ряды
![]() и
и![]() расходятся. Что можно сказать о сходимости
ряда
расходятся. Что можно сказать о сходимости
ряда![]() ?
Проиллюстрируйте Ваши предположения
на примерах, используя М-файл из упр. 1.
?
Проиллюстрируйте Ваши предположения
на примерах, используя М-файл из упр. 1.
Признаки сходимости рядов с положительными членами
Рассмотрим некоторые признаки сходимости числовых рядов.
|
Признак
сравнения.
Пусть даны два ряда
1) если ряд (2) («больший») сходится, то и ряд (1) («меньший») сходится; 2) если ряд (1) («меньший») расходится, то и ряд (2) («больший») расходится. |
Например, рассмотрим
ряд
![]() ,
полученный из ряда
,
полученный из ряда![]() (упр. 1, п. 5) отбрасыванием первых двух
членов. Его можно сравнить с рядом
(упр. 1, п. 5) отбрасыванием первых двух
членов. Его можно сравнить с рядом![]() ,
сходимость которого ранее доказана
(упр. 1, п.6). Так как
,
сходимость которого ранее доказана
(упр. 1, п.6). Так как![]() и «больший» ряд сходится, то сходится
и «меньший» ряд
и «больший» ряд сходится, то сходится
и «меньший» ряд![]() ,
а, значит, и ряд
,
а, значит, и ряд![]() .
.
|
Предельный признак сравнения.
Пусть даны два
ряда
1) если один из рядов сходится, то сходится и другой; 2) если один из рядов расходится, то расходится и другой. |
Докажем, что
расходится (гармонический)
ряд
![]() (упр. 1 п. 4). Используем для сравнения ряд
(упр. 1 п. 4). Используем для сравнения ряд![]() .
Заметим, что
.
Заметим, что![]() и найдем частичные суммы ряда
и найдем частичные суммы ряда![]() :
:![]()
![]()
![]() .
Отсюда следует, что
.
Отсюда следует, что![]() ,
т.е. ряд
,
т.е. ряд![]() расходится. Но
расходится. Но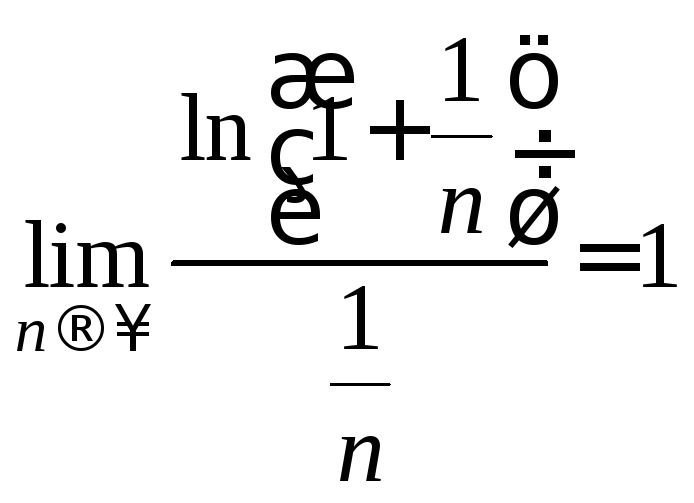 ,
значит, из расходимости ряда
,
значит, из расходимости ряда![]() следует расходимость ряда
следует расходимость ряда![]() .
.
|
Признак Даламбера. Если
для ряда
|
Рассмотрим ряд
![]() .
.
Имеем
![]() ,
следователь, ряд сходится.
,
следователь, ряд сходится.
|
Радикальный признак Коши. Если
для ряда
|
Рассмотрим ряд
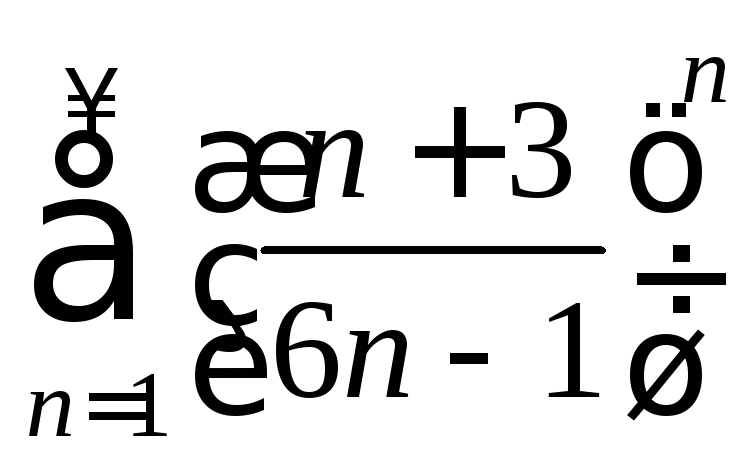 .
.
Имеем
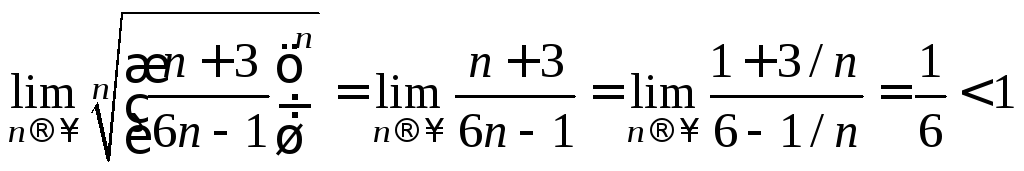 ,
следователь, ряд сходится.
,
следователь, ряд сходится.
|
Интегральный признак Коши.
Пусть функция
|
Выясним, при каких
![]() сходится ряд
сходится ряд![]() .
Положим
.
Положим![]() (
(![]() ).
Функция
).
Функция![]() положительна, монотонно убывает. Поэтому
ряд
положительна, монотонно убывает. Поэтому
ряд![]() сходится тогда и только тогда, когда
сходится интеграл
сходится тогда и только тогда, когда
сходится интеграл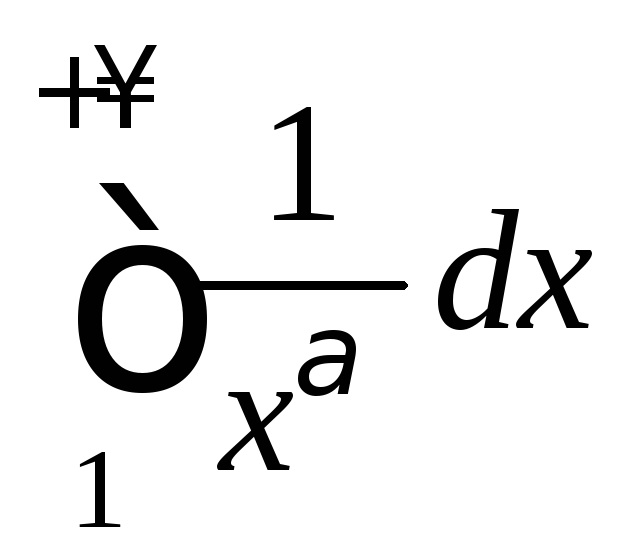 .
Этот интеграл сходится при
.
Этот интеграл сходится при![]() и расходится при
и расходится при![]() .
Значит, и ряд
.
Значит, и ряд![]() сходится при
сходится при![]() и расходится при
и расходится при![]() .
.
Упражнение 5. Опираясь на признаки сходимости, доказать:
а) ряд
![]() расходится; б) ряд
расходится; б) ряд![]() сходится;
сходится;
в) ряд
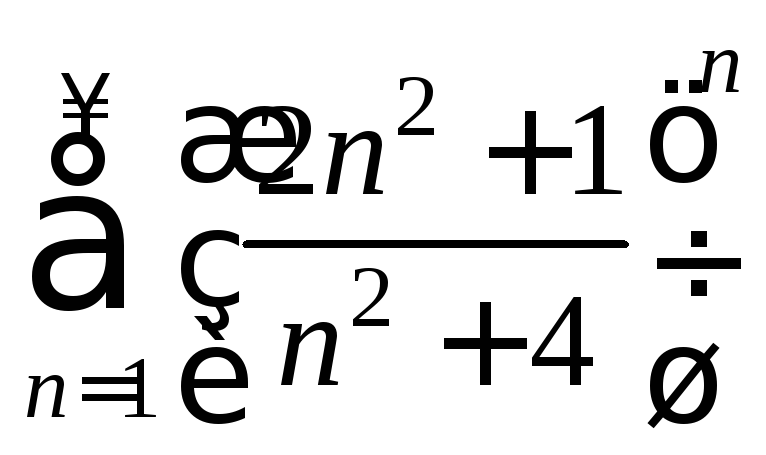 расходится; г) ряд
расходится; г) ряд![]() сходится.
сходится.

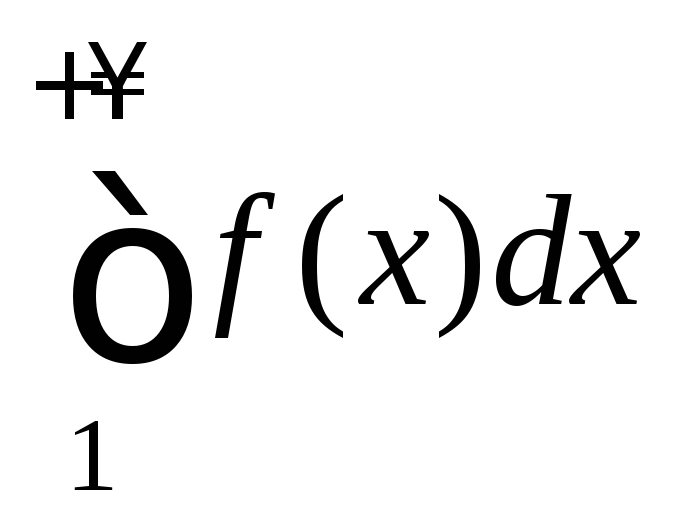 (иными словами ряд
(иными словами ряд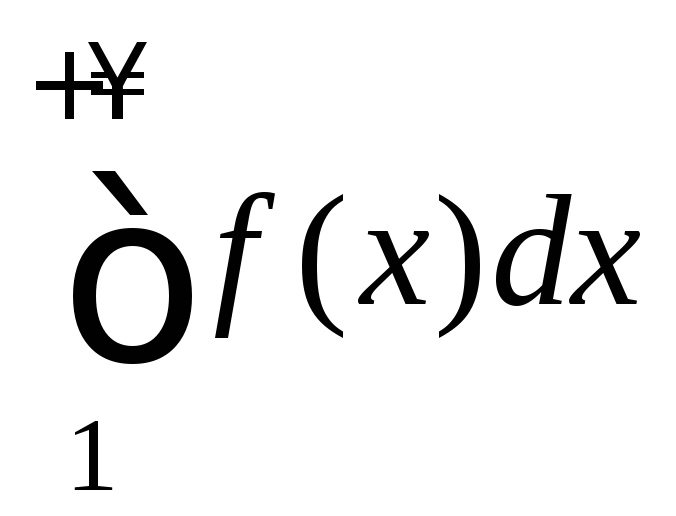 ).
).