Lektsia-3_1

3. ПОЛЕ СИЛЫ ТЯЖЕСТИ ЗЕМЛИ

3.1. Гравитационный потенциал

Закон всемирного тяготения для точечных масс:

Напряженность гравитационного поля или ускорение силы тяжести, создаваемое точечной массой , равно

.

Гравитационное поле является центральным. Для него справедлив принцип суперпозиции.

Как и для электростатического поля, для гравитационного поля легко доказывается интегральная теорема Гаусса

.

Отсюда немедленно следует, что если распределение масс центрально симметричное, то величина ускорения силы тяжести в данной точке определяется только массой шара, на поверхности которого находится эта точка. Применительно к бесконечной сферически однородной и изотропной Вселенной это приводит к так называемому гравитационному парадоксу: ускорение силы тяжести в данной точке зависит от выбора начала системы отсчета.

Первое дифференциальное уравнение для гравитационного поля получается из интегральной теоремы Гаусса-Остроградского

,

где – плотность, – объем внутри . Отсюда

.

Второе дифференциальное уравнение – это дифференциальное условие потенциальности гравитационного поля:

.

Непосредственным вычислением (проще всего в сферических координатах) можно показать, что ротация любого центрального поля равна нулю.

Поскольку по вычислению, то можно ввести гравитационный (ньютоновский) потенциал, такой, что

.

Для материальной точки массы M (а также для сферически симметричного тела)

.

Для объемного тела с произвольным распределением плотности

.

Поскольку , то гравитационный потенциал в области, где , удовлетворяет уравнению Пуассона

,

а в области, где , уравнению Лапласа

.

Вне Земли и на ее поверхности гравитационный потенциал удовлетворяет уравнению Лапласа, которое в сферических координатах имеет вид:

.

Фундаментальным внешним решением этого уравнения является сферический гармонический ряд

где 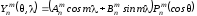– сферические функции порядка и степени 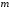; 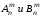– константы, определяемые из граничных условий; – присоединенные функции Лежандра:

Это система ортонормированных функций, т.е.

– нормировочный множитель.

На поверхности сферы сферические функции имеют знакочередующиеся минимумы и максимумы (см. рис.), области которых определяются пересечением широтных линий и меридиональных линий.

Функции с называются зональными гармониками ( примеры на рис.); если , то это секториальные гармоники (пример ); и, наконец, если , то это тессеральные гармоники (пример ). На рисунках представлены полусферы.

Целесообразно в разложении потенциала выделить первый член: , вынести его за скобки и нормировать на экваториальный радиус Земли :

.

Введем также новые постоянные

.

В силу того, что для любых , то . Окончательно,

.

Элементы гравитационного потенциала Земли вычисляют из анализа изменений элементов орбит искусственных спутников. Если бы спутники летали в поле силы тяжести материальной точки, то их движение было бы чисто кеплеровым (стационарная эллиптическая орбита). Однако элементы их орбит (эксцентриситет, наклонение, положение узлов и т.д.) изменяются с течением времени, и по этим изменениям можно вычислить коэффициенты и . Вот их первые значения (в единицах ):

и т.д.

Видно, что гравитационный потенциал Земли определяется в основном двумя членами: потенциалом материальной точки и зональной гармоникой 2-го порядка

,

которая обусловлена полюсным сжатием Земли.

3.2. Формула (теорема) Мак-Кулло

Докажем теорему:

Гравитационный потенциал тела массой , слабо отклоняющегося от сферической симметрии равен

,

где – моменты инерции тела относительно главных осей, 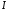– момент инерции относительно оси, направленной из центра масс в точку наблюдения.

Доказательство теоремы.

Начало координат поместим в центр масс тела (см. рис.). – текущие координаты материальных точек тела, – фиксированные координаты точки наблюдения.

.

.

Воспользуемся разложением в ряд Тейлора квадратного трехчлена (см. справочник по высшей математике):

.

Именно здесь предполагаем, что 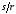всегда мало, и оставляем в разложении только первые члены. Тогда

.

– объем тела, . Нет необходимости предполагать постоянство плотности.

Считаем интегралы.

1). – ньютоновский потенциал (M – масса тела).

2). Второй интеграл равен нулю. Действительно

,

,

а эти интегралы дают координаты центра масс, которые по условию равны нулю.

3). Это следует из определения главных моментов инерции.

4) – момент инерции тела относительно оси OP.

Итак, . Теорема доказана.

Для однородного (и даже неоднородного, но сферически симметричного) шара все моменты инерции равны между собой и .

С достаточно хорошим приближением Земля представляет собой двухосный эллипсоид вращения с полярным моментом инерции и экваториальными моментами инерции .

Если – направляющие косинусы оси OP относительно выбранных осе координат, то с учетом того, что 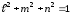, и , формулу Мак-Кулло нетрудно преобразовать к виду

.

Если обратиться снова к разложению гравитационного потенциала в ряд по сферическим функциям и принять осевую симметрию Земли, то в этом разложении останутся только зональные гармоники:

Сравнивая с тем, что получено по формуле Мак-Кулло, получаем

.

Для , , имеем . Из спутниковых наблюдений (геодезический спутник Lageos)

.

3.3. Геопотенциал. Геоид

Помимо силы всемирного тяготения, действующей со стороны Земли, на все тела на ее поверхности действует также и центробежная сила, направленная перпендикулярно оси вращения. Радиальная составляющая центробежного ускорения равна

.

По порядку величины на поверхности Земли

.

Это не малая величина с геофизической точки зрения.

Целесообразно ввести центробежный потенциал

.

Тогда

.

Геопотенциалом называют сумму ньютоновского и центробежного потенциалов:

.

Ускорение силы тяжести на вращающейся Земле определяют как градиент геопотенциала:

.

При осевой симметрии

.

Второй член под корнем приблизительно в 300 раз меньше первого, поэтому в теории (но не на практике!) обычно принимают

.

Геоид – это поверхность равного геопотенциала, отнесенная к уровню Мирового океана. Уравнение поверхности геоида в первом приближении имеет вид:

,

где – экваториальный радиус Земли, – географическая широта (), –

геодезическое сжатие,

.

Средний радиус Земли определяют как среднее геометрическое полярного и экваториального радиусов: .

Физическая поверхность Земли заметно не совпадает с геоидом. Достаточно заметить, что горы вздымаются над уровнем моря на высоту до 9 км, а экваториальное вздутие Земли всего 21,385 км. Планетарные особенности земной поверхности хорошо видны из приведенной ниже гипсометрической диаграммы.

Средние уровни суши – 840 м, дна океана – 3800 м. Абиссаль, абиссальное ложе, шельф.

Удивительно, что такие вот особенности рельефа Земли спутники не «чувствуют» в своем полете.

Принцип изостатической компенсации масс был высказан в середине XIX века, когда геодезические измерения в Северной Индии показали, что Гималаи вызывают значительно меньшее отклонение отвеса, нежели можно было ожидать от такой массы, возвышающейся над поверхностью Земли. Согласно гипотезам Эри, Пратта и Венинг Мейнеса, различающимися деталями распределения плотностей в нижней части горных массивов, менее плотные возвышенные части земной коры «плавают» в более плотной нижней литосфере как пробка в воде. Закон Архимеда.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Доказать интегральную теорему Гаусса для напряженности гравитационного поля, создаваемого точечной массой.

2. Показать, что

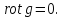
3. В декартовых координатах показать, что где – произвольная дифференцируемая скалярная функция.

4. Показать, что если имеет место сферически симметричное распределение плотности в некотором объеме Ω (т.е. ), то гравитационное поле, создаваемое массой M, сосредоточенной в этом объеме, имеет такой же вид, как поле точечной массы M, сосредоточенной в центре объема Ω.

Эта задача имеет целью показать, почему для определения ускорения силы тяжести (напряженности гравитационного поля) на поверхности Земли используется закон всемирного тяготения, который справедлив для точечных масс.

5. Показать, что момент инерции однородного шара радиуса R и массы M относительно любой из осей, проходящих через центр шара, равен (2/5)MR².

6. Показать, что момент инерции неоднородного шара радиуса R со сферически симметричным распределением плотности, т.е. , относительно любой из осей, проходящих через центр шара, также равен (2/5)MR², где M – масса шара.

7. Исследовать уравнение поверхности геоида _. Оценить, каковы максимальные отклонения геоида от эллипсоида вращения с полуосями

.

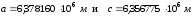8. Горное плато (типа Памира или Тибета) в среднем имеет высоту 4 км над уровнем моря. На какой глубине располагается подошва этого плато (граница Мохо)? Плотность пород, слагающих горное плато принять равной 2,7 г/см³, а плотность пород верхов мантии (слоя В по Буллену) – равной 3,3 г/см³.

35