
- •Поле двух бесконечных параллельных разноименно заряженных плоскостей
- •1. Поле равномерно заряженной сферической поверхности
- •2. Поле объемно заряженного шара
- •3. Поле равномерно заряженной бесконечной плоскости
- •4. Поле равномерно заряженного бесконечного цилиндра (нити)
- •6. Работа сил электростатического поля в случае двух точечных зарядов. Потенциал. Потенциал поля, создаваемого системой точечных зарядов.
- •7.Циркуляция вектора напряженности электрического поля. Связь между напряжённостью электростатического поля и потенциалом.
- •8.Эквипотенциальные поверхности, их связь с силовыми линиями.
- •9.Проводники и диэлектрики. Заряженный проводник. Проводник во внешнем электрическом поле.
- •10. Электроёмкость, конденсаторы. Электроёмкость проводящего шара. Ёмкость плоского конденсатора, сферического конденсатора, цилиндрического конденсатора.
- •После интегрирования получим
- •Энергия заряженного конденсатора
- •3.2. Напряженность электростатического поля двух
- •3.3. Поле равномерно заряженной сферической поверхности
- •4. Уравнения Пуассона и Лапласа
- •Электрический диполь
- •2.1. Неполярные диэлектрики
- •2.2. Полярные диэлектрики
- •Поляризация диэлектрика
- •Электрическое поле в диэлектриках
- •17.Теорема Гаусса для поля вектора поляризации. Теорема Гаусса для поля вектора электрического смещения. Связь между векторами d и e.
- •2.6.2. Теорема Гаусса для поля вектора электрического смещения
- •2.7. Связь между векторами и
- •Сила тока, плотность тока
- •Уравнение непрерывности
- •Закон Ома для однородного участка цепи
- •20,Сторонние силы. Закон Ома для неоднородного участка цепи.
- •21,Работа, мощность, кпд источника тока. Тепловое действие тока. Закон Джоуля-Ленца.
- •22,Переходные процессы в конденсаторах. Правила Кирхгофа.
- •Первое правило Кирхгофа
- •5.9.2. Второе правило Кирхгофа
- •23,Источники магнитного поля. Сила взаимодействия, движущихся зарядов.
- •24,Магнитное поле движущего заряда. Магнитный поток.
- •26,Магнитное поле соленоида. Проводник с током в магнитном поле. Взаимодействие параллельных токов. Движение заряженных частиц в магнитном поле. Магнитное поле соленоида
Закон сохранения заряда. Закон Кулона.
сила взаимодействия точечных зарядов пропорциональна величине взаимодействующих зарядов и обратно пропорциональна квадрату расстояния между ними, т.е.:
 ,
,
Единичный вектор – это вектор, модуль которого равен единице.
Следовательно:
 ,
,
Силу Кулона, действующую на заряд 1 со стороны заряда 2, можно записать как

 .
.
На заряд 2 со стороны заряда 1 действует сила
 .
.
выражение для силы взаимодействия электрических зарядов в вакууме имеет следующий вид:
 .
.
Электрическое поле. Напряжённость электрического поля. Принцип суперпозиции электрических полей. Графическое изображение электрических полей.

где
 – напряженность
электрического поля
– напряженность
электрического поля 
если имеется несколько точечных зарядов, то сила взаимодействия каждой пары зарядов определяется законом Кулона и не зависит от электрических полей, создаваемых другими зарядами. Из сказанного вытекает, что если есть N зарядов, то сила, действующая на заряд с номером k со стороны всех остальных, равна векторной сумме
 ,
Это утверждение
носит название принципа
суперпозиции (наложения) электрических
полей.
,
Это утверждение
носит название принципа
суперпозиции (наложения) электрических
полей.
Принцип суперпозиции электрических полей утверждает, что напряженность электрического поля системы зарядов равна векторной сумме напряженностей полей, создаваемых каждым из зарядов системы в отдельности (1.9):

Чтобы получить наглядное представление об электрическом поле, его можно изобразить с помощью линий напряженности электрического поля (их называют также силовыми линиями). Линия напряженности – это линия, касательная к которой в каждой точке совпадает с направлением напряженности электрического поля в данной точке. Линии напряженности выходят из положительного заряда и уходят в бесконечность, либо заканчиваются на отрицательном заряде. В том месте, где модуль напряженности поля больше, линии проводят гуще, меньше – реже, так, что густота линий пропорциональна модулю напряженности.
3.
Поток
вектора напряжённости электрического
поля. Теорема Гаусса.
Здесь
 – вектор единичной нормали к поверхностиS.
– вектор единичной нормали к поверхностиS.
Поток
вектора
 через площадку
через площадку по определению равен:
по определению равен:
 ,
,


Поток через всю поверхность, примерно, равен сумме потоков через отдельные элементы:
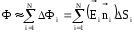 .
.
В пределе, когда площадь элемента выбирается все меньше, а число элементов N стремится к бесконечности, выражение для потока переходит в интеграл:
 .
.
Вычислим поток вектора напряженности электрического поля через замкнутую поверхность. Первоначально будем считать, что поверхность – сфера, а в центре ее находится точечный заряд q

4.Применение теоремы Гаусса для расчёта электрических полей. (Типы распределения заряда. Поле бесконечной равномерно заряженной плоскости).
Типы распределения заряда:
1)Линейная
плотность заряда:
 [] =
Кл/м.
[] =
Кл/м.
2)Поверхностная
плотн зар:
 [
[ ]
= Кл/м2.
]
= Кл/м2.
3)Объемная
плотн зар:
 ,
[
,
[ ]
= Кл/м3.
]
= Кл/м3.
Поле бесконечной равномерно заряженной плоскости:
Если заряд распределен в тонком поверхностном слое заряженного тела, то его можно охарактеризовать поверхностной плотностью заряда. Поверхностная плотность заряда – это заряд, приходящийся на единицу площади поверхности:
 .
.
В случае равномерно заряженнойплоскости, напряженность электрического поля перпендикулярна плоскости.Выберем на плоскости площадкуSи построим «гауссов ящик», как показано на рис..
Боковые
поверхности перпендикулярны площадке
Sи параллельны вектору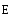 .
Подсчитаем поток вектора напряженности
электрического поля: на боковой
поверхности
.
Подсчитаем поток вектора напряженности
электрического поля: на боковой
поверхности так как вектор
так как вектор параллелен боковой поверхности, на
торцах
параллелен боковой поверхности, на
торцах .
Следовательно, поток равен (см. рис.
2.3):
.
Следовательно, поток равен (см. рис.
2.3):


Найдем суммарный заряд внутри ящика. Ясно, что это заряд на площадке S, значит:
 .
.
На основании теоремы Гаусса (2.3) получаем:
 ,
,
откуда следует – напряженность электрического поля, создаваемого бесконечной заряженной плоскостью, по модулю равна:
 .
.
5.Поле двух бесконечных, разноимённо заряженных плоскостей. Поле равномерно заряженной сферической поверхности. Поле равномерно заряженного шара. Напряжённость электрического поля бесконечной равномерно заряженной нити).
Поле двух бесконечных параллельных разноименно заряженных плоскостей
(рис. 127). Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями +σ и −σ. Поле таких плоскостей найдем как суперпозицию полей, создаваемых каждой из плоскостей в отдельности.
На рисунке верхние стрелки соответствуют полю от положительно заряженной плоскости, нижние — от отрицательной плоскости. Слева и справа от плоскостей поля вычитаются (линии напряженности направлены навстречу друг другу), поэтому здесь напряженность поля E = 0
В области
между плоскостями E+ + E− (E+ и
E− определяются
по формуле ![]() ),
поэтому результирующая напряженность:
),
поэтому результирующая напряженность: ![]() .
.
Таким образом, результирующая напряженность поля в области между плоскостями описывается этой формулой, а вне объема, ограниченного плоскостями, равна нулю.

1. Поле равномерно заряженной сферической поверхности
|
Рис. 1.10. Электрическое поле заряженной сферы |
Сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверхностной плотностью . Благодаря
равномерному распределению заряда
по поверхности поле, создаваемое им,
обладает сферической симметрией.
Поэтому линии напряженности направлены
радиально (рис. 1.10, а).
Напряженность поля будет, таким
образом, одинакова во всех точках
воображаемой сферы радиуса r,
концентричной с заряженной сферой.
Поскольку напряженность
поля |
|
|
Если r < R, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности Е = 0. График зависимости Е от r приведен на рис. 1.10, б.
2. Поле объемно заряженного шара
Шар радиуса R с общим зарядом Q заряжен равномерно с объемной плотностью r.
Учитывая соображения симметрии, при r R получим, как и в случае сферической поверхности:
|
|
(rR). |
|
Рис. 1.11. Зависимость напряженности поля равномерно заряженного шара от расстояния r |
Внутри шара при r < R, Q = 4/3 r 3. Поэтому, согласно теореме Гаусса | |
|
| ||
|
Учитывая, что =Q/(4/3 R3), получим | ||
|
|
(r R). | |
|
График зависимости E от r приведен на рис. 1.11.
| ||
3. Поле равномерно заряженной бесконечной плоскости
|
Рис.1.12. Электрическое поле равномерно заряженной плоскости |
Бесконечная плоскость заряжена с постоянной плотностью +. Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Поскольку через боковую поверхность цилиндра поток равен нулю, весь поток проходит сквозь его основания (рис. 1.12 а). По теореме Гаусса
Отсюда напряженность электрического поля равна
График зависимости E от r приведен на рис. 1.12 б. |
4. Поле равномерно заряженного бесконечного цилиндра (нити)
|
Рис. 1.13. Электрическое поле равномерно заряженного цилиндра |
Бесконечный цилиндр радиуса R заряжен равномерно; линейная плотность заряда равна l. Из соображений симметрии следует, что линии напряженности будут направлены по радиусам круговых сечений с одинаковой густотой во все стороны относительно оси цилиндра. В качестве замкнутой поверхности мысленно построим коаксиальный с заряженным цилиндр радиуса r и высотой l (рис. 1.13 а). Поскольку вектор напряженности параллелен торцам, поток сквозь основания цилиндра равен нулю, и
Отсюда при r R
Если r < R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области Е = 0. График зависимости E от r приведен на рис. 1.13 б.
|


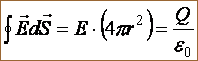 или
или .
.


 ,
,




 .
. .
.