1)

Функция (отображение, оператор, преобразование) — математическое понятие, отражающее связь между элементами множеств. Другими словами, функция — это правило, по которому каждому элементу одного множества (называемогообластью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Область определения функции — множество, на котором задаётся функция. В функции "y = f (x)" Это все значения, которые может принимать x.

Область значений функции — множество значений, которые принимает функция в результате её применения.

Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.

При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции.

Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.

Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.

Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.

Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции.

Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.

Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью.

Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде.

Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно.

• График функции — множество точек, у которых абсциссы являются допустимыми значениями аргумента x, а ординаты — соответствующими значениями функции .

• Нечётная функция — функция, меняющая значение на противоположное при изменении знака независимой переменной (график ее симметричен относительно центра координат).

• Чётная функция — функция, не изменяющая своего значения при изменении знака независимой переменной (график еесимметричен относительно оси ординат).

• Ни чётная, ни нечётная функция (функция общего вида) — функция, не обладающая симметрией. В эту категорию относят функции, не подпадающие под предыдущие 2 категории.

Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное^[1]. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении

ОГРАНИЧЕННЫЕ ФУНКЦИИ Пусть задана функция y=f(x), определенная на некотором множестве D значений аргумента. Функция y=f(x) называется ограниченной на множестве D, если существует положительное число М такое, что для всех значений x из рассматриваемого множества, выполняется неравенство |f(x)|≤M. Если же такого числа М не существует, то функция f(x) называется неограниченной на множестве D.

СЛОЖНАЯ ФУНКЦИЯ

- функция, представленная как композиция нескольких функций.

2)

Теорема Лопита́ля (также правило Бернулли — Лопиталя^[1]) — метод нахождения пределов функций, раскрывающий неопределённости вида и . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.

Теорема Лопиталя:

Если:

1.  или ;

2.  и дифференцируемы в окрестности;

3.  в окрестности ;

4. существует ,

то существует .

Примеры

• 

• 

3)

Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум —точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).

(Необходимое условие экстремума)

Если функция имеет экстремум в точке, то ее производнаялибо равна нулю, либо не существует.

(Первое достаточное условие экстремума)

Пусть для функции выполнены следующие условия:

1. функция непрерывна в окрестности точки ;

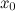2.  или не существует;

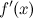3. производная при переходе через точкуменяет свой знак.

(Второе достаточное условие экстремума)

Пусть для функции выполнены следующие условия:

1. она непрерывна в окрестности точки ;

2. первая производная в точке;

3.  в точке .

4)

Функция называется непрерывной на отрезке, если она непрерывна во всех точках интервала, непрерывна справа в точкеи непрерывна слева в точке.

Функции, непрерывные на отрезке, обладают рядом замечательных свойств, к изложению которых мы сейчас приступим.

Сначала мы сформулируем теоремы, выражающие эти свойства, и разъясним их на графиках и примерах, а затем докажем их формально.

Т е о р е м а  1. Если функция непрерывна на отрезке, то она ограничена на нем,

Теорема 2.  Если функция непрерывна на, то существует ее минимум и максимум на

Теорема 3.Если функция непрерывна на отрезке  и числа  и  не равны нулю и имеют разные знаки, то на интервале  имеется по крайней мере одна точка  такая, что 

5)

Б.м. функции иназываютсяэквивалентными или равносильными б.м. одного порядка при , если

Обозначают: при.

Таблица эквивалентных б.м. функций

Таблица эквивалентных б.м. функций при 

6)

Понятие непрерывности функции в точке

Функция называется непрерывной в точке , если:

1. функция определена в точке и ее окрестности;

2. существует конечный предел функции 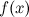в точке ;

3. это предел равен значению функции в точке , т.е. 

Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.

Точки разрыва функции и их классификация

Точка , в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:

1. функция определена в точке и ее окрестности;

2. существует конечный предел функции в точке ;

3. это предел равен значению функции в точке , т.е. 

называется точкой разрыва функции.

Точка разрыва первого рода

Если в точке существуют конечные пределы и , такие, что , то точка называется точкой разрыва первого рода.

Точка разрыва второго рода

Если хотя б один из пределов или не существует или равен бесконечности, то точка называется точкой разрыва второго рода.

Точка устранимого разрыва

Если существуют левый и правый пределы функции в точке и они равны друг другу, но не совпадают со значением функции в точке : или функция не определена в точке , то точка называется точкой устранимого разрыва.

7)

Производной от функции в точке называется предел отношения приращения функции к приращению аргумента  :  при , если он существует, то есть:

или

Геометрический смысл производной

Производная функции , вычисленная при заданном значении , равна тангенсу угла, образованного положительным направлением оси и положительным направлением касательной, проведенной к графику этой функции в точке с абсциссой 

Физический

смысл производной.

Если точка движется вдоль оси х и ее координата изменяется по закону  x(t), то мгновенная скорость точки:

8)

Асимптоты графика функции

Виды асимптот

Прямая называется вертикальной асимптотой графика функции .

Прямая называется горизонтальной асимптотой графика функции .

Прямая называется наклонной асимптотой графика функции .

9)

Понятие функции одной переменной

Рассмотрим два числовых множества X и Y. Правило f, по которому каждому числу хI Х ставится в соответствие единственное число yI Y, называется числовой функцией, заданной на множестве Х и принимающей значения во множестве Y.

Таким образом, задать функцию, значит задать три объекта:

1) множество Х (область определения функции);

2) множество Y (область значений функции);

3) правило соответствия f (сама функция).

Если независимая переменная и функциясвязаны уравнением вида, которое не разрешено относительно, то функцияназываетсянеявной функцией переменной .

Несмотря на то, что уравнение не разрешимо относительно , оказывается возможным найти производную от по . В этом случае необходимо продифференцировать обе части заданного уравнения, рассматривая функцию как функцию от , а затем из полученного уравнения найти производную .

10)

Бесконечно малые и бесконечно большие величины.

Понятие бесконечно малых и бесконечно больших величин играет важную роль в математическом анализе. Многие задачи просто и легко решаются используя понятия бесконечно больших и малых величин.

Бесконечно малые.

Переменная называется бесконечно малой, если для любого существует такое значение , что каждое следующии за ним значение будет по абсолютной величине меньше .

Если - бесконечно малая то говорят, что стремится к нулю, и пишут: .

Бесконечно большие.

Переменная x называется бесконечно большой, если для всякого положительного числа cсуществует такое значение , что каждое следующее за ним x будет по абсолютной величине больше . Пишут: 

Величина, обратная к бесконечно большой, есть величина бесконечно малая, и обратно. 

СВОЙСТВА!!!!!!!!!! 1)Обратная к бесконечно малой величине,это бесконечно большая.  2)Обратная к ББ величине,этобесконечно малая. . 3)произведение ограниченной послед-ти на бесконечно малую это бесконечно малая величина.  4)Сумма огр-ой послед-ти и бесконечно большой величины это бесконечно большая величина. .

11)