Vse_bomby_s_dokazatelstvami

1. Теорема Больцано-Вейрштрасса.

Из любой огрпосл-сти можно выделить сх-сяподпоследовательность. Доказательство. Пусть {xn} - ограниченная последовательность, тогда все члены последовательности принадлежат некоторому отрезку, т.е.

Разобьем отрезок = [a,b] пополам точкой d. Тогда по крайней мере один из отрезков [a,d],[d,b] содержит бесконечное число членов последовательности {xn}. Если оба отрезка обладают этим свойством, возьмем, например, правый отрезок (и будем так поступать в дальнейшем). Выбранный отрезок, содержащий бесконечное число членов данной последовательности, обозначим 1 = [a1,b1], его длина равна

.

Разделив отрезок 1 пополам, выберем указанным выше способом из двух получившихся отрезков отрезокΔ2 = [a2,b2], содержащий бесконечное число членов последовательности {xn}. Продолжая эти рассуждения, получим последовательность {Δn = [an,bn]} отрезков таких что:

при

Следовательно, {Δn} - стягивающаяся последовательность отрезков. По теореме Кантора существует единственная точка c, принадлежащая всем отрезкам, т.е., Покажем, что найдется подпоследовательность

последовательности{xn}: .Так как отрезок 1 содержит бесконечное число членов последовательности {xn}, то. Отрезок 2 также содержит бесконечное число членов данной последовательности, и поэтому.

Вообще,, где . Следовательно, существуетподпоследовательность последовательность {xn} такая, чтоУсловия (2) и (4) означают, что точки c и принадлежит отрезку Δk = [ak,bk], и поэтому расстояние между ними не превосходит длины отрезка Δk, т.е.

.

Так как - бесконечно малая посл-сть, следует утверждение теоремы.

Критерий Коши сходимости числовой последовательности.

Для того чтобы последовательность имела конечный предел, необходимо и достаточно, чтобы она былафундаментальной .

Необходимость. Пусть последовательность {xn} имеет конечный предел a.

По определению предела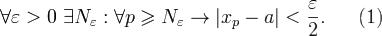

Пологая в (1) сначала p = n, а затем p = m и используя неравенство для модуля суммы (разности), получаем

Следовательно для любого и для любого выполняется неравенство , т.е последовательность явл. фундаментальной. Достаточность. Пусть {xn} - фундоментальная последовательность. Докажем, что она имеет конечный предел. По определению фундоментальной последовательности

Так как фундометальная последовательность {xn} является ограниченной, то по теореме Больцано-Вейерштрасса она содержит сходящуюся

подпослед-сть . Пусть её предел равен a, т.е. Покажем, что число a является пределом

исходнойпоследовательности {xn}. По определению предела (3)

Пусть . Фиксируем в (4) номер . Тогда при m = nk и

при всех в силу (2) выполнется неравенство. Из (4) и (5) следует, что при всех 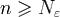справедливо неравенство

, т.е.

2.Теорема Вейерштрасса. Функция, непрерывная на отрезке, ограничена и достигает своих верхней и нижней граней.

Доказательство. Пусть.

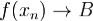По определению верхней грани Следовательно, при .

Последовательность {xn} ограничена, так как . По теореме Больцано-Вейерштрасса выделим из неё сходящуюся подпоследовательность , при . Переход к пределу в неравенстве , получаем, что . В силу непрерывности функции f в точке x0 имеем при .

С другой стороны, - подпоследовательность сходящейся

к B последовательности. Поэтому при . Из последних двух соотношений получаем, что.

Отсюда следует, во-первых, что , т.е. что функция f ограничена сверху, и, во-вторых, что функция достигает своей верхней грани в точке x0. Аналогично можно доказать, что функция f ограничена снизу и достигает своей нижней грани. Теорема доказана.

3. Теорема о промежуточных значениях непрерывной функции.Пусть функция непрерывна на отрезке [a,b], f(a) = A, f(b) = B. Пусть C находится между A и B.Тогда

Доказательство.Пусть, для определенности, . Поделим отрезок [a,b] пополам и через[a1,b1] обозначим такую его половину, для которой . Поделим отрезок пополам и через [a2,b2] обозначим такую его половину, для которой . Продолжая процесс, получим стягивающуюся систему вложенных отрезков {[an,bn]}, для которых.

Пусть . Тогда при , и (в силу непрерывности функции f в точке ξ)

при .

Переходя к пределу в последнем неравенстве, получаем ,что и требовалось доказать.

4. Теорема Ролля.Пусть функция f:

1. непрерывна на [a,b];2. дифференцируема на (a,b);3. f(a) = f(b). Тогда .

Доказательство. Случай тривиален. Будем считать далее, что . По теореме Вейерштрасса в некоторых точках

отрезка [a,b] функция f принимает максимальное и минимальное значения. По крайней мере, одна из этих точек лежит на интервале (a,b), так

как min[a,b]f <max[a,b]f. Тогда по теореме Ферма производная f' в этой точке равна нулю, что и требовалось доказать.

Теорема Лагранжа.Если функция f(x) непрерывна на отрезке [a,b] и дифференцируема на интервале (a,b), то в этом интервале найдется хотя бы одна точка ξ: Доказательство.Рассмотрим функцию

где число λ выберем таким, чтобы выполнялось условие , т.е. f(a)

+ λa = f(b) + λb. Отсюда находим

Так как функция непрерывна на отрезке [a,b], дифференцируема на интервале (a,b) и принимает равные значения в концах этого интервала, то по теореме Ролля существует точка такая, что .

Отсюда в силу (2) получаем равносильное равенству (1). Теорема Коши.Если функции f(x) и g(x) непревны на отрезке [a,b], дифференцируемы на интервале (a,b), причем во всех точках этого

интервала, то найдется хотя бы одна точка :. Доказательство.Рассмотрим функцию где число λ выберем таким, чтобы выполнялось равенство ,

которое равносильно следующему: Заметим, что , так как в противном случае согласно теореме Ролля существовала бы точка такая что g'(c) = 0 вопреки условиям теоремы.

Итак, и из равенства (1) следует, что

Так как функция при любом λ непреына на отрезке [a,b] и дифференцируема на интервале (a,b), а при значение λ определяемом формулой (2), принимает равные значения в точках a и b, то по теореме

Ролля существует точка такая, что , откуда . Из этого равенства следует утверждение теоремы.

5. Остаточный член формулы Тейлора.

Пусть . Тогда в некоторой окрестности U(x0) можно написать

, которое называется формулой Тейлора функции f в точке x0,

где Pn(f,x) называется многочленом Тейлора, аrn(f,x) - остаточным членом Тейлора (после n-го члена).

Если существует,то согласно определению сходимости ряда

(1) сходится к функции f(x) в точке x.

ЛеммаПусть в . Тогда в верно

Доказательство:

Теорема. Формула с остаточным членом в форме Лагранжа.

Пусть x > x0(x < x0), непрерывна на отрезке [x0,x]([x,x0]), на интервале (x0,x)((x,x0)). Тогда справедлива формула (1), в которой

, 0 < θ < 1. Доказательство: будем проводить по индукции, считая x > x0. При n =

0 теорема утверждает, что при некотором

Это утверждение верно, так как оно совпадает с доказанной ранее формулой конечных приращений Лагранжа.

Предположим, что утверждение верно при и установим, что оно верно и при n. Использую теорему Коши о среднем и лемму, имеем (для определенности x > x0)

где x0 < η < ξ < x,а предпоследнее равенство написано в силу предположения индукции.Теорема доказана.

Теорема. Формула Тейлора с остаточным членом в форме Пеано.

Пусть и . Тогда справедлива формула (1), в которо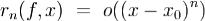й при . Доказательство: будем проводить по индукции:

При n = 1 утверждение теоремы верно. В самом деле, в этом случае f дифференцируема в точке x0. Следовательно,

Что совпадает с условием теоремы.Предположим, что утверждение теоремы верно при и покажем, что это верно и для n. Использую теорему Лагранжа о конечных приращениях и лемму, имеем (считая для определенности x > x0): 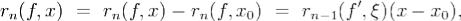где x0 < ξ < x.

По предположению индукции при . Следовательно, при .Ч.т.д.

6. Исследование функций одной переменной при помощи первой и второй производных на монотонность, локальные экстремумы, выпуклость.

Теорема1Пусть f дифференцируема на (a,b). Тогда

1.условие на (a,b) необходимо и достаточно для того, чтобы функция f возрастала (убывала) на (a,b);

2.условие f' > 0(f' < 0) на (a,b) достаточно, чтобы функция f строго возрастала (строго убывала) на (a,b).

Доказательство:Достаточность следует из формулы конечныхприрощений

Лагранжа Необходимость. Пусть f возрастает на

Тогда . Следовательно, Замечание: условие f' > 0 не является необходимым. Пример:

Теорема 2. Ферма.Пусть x0 - точка экстремума функции f. Тогда производная f'(x0) либо не существует, либо f'(x0) = 0.

Доказательство:Пусть для определенности 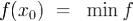. Тогда

при Δx > 0 и при Δx < 0. Переходя в этих неравенствах к пределу при , получаем соответственно , . Отсюда следует, что f'(x0) = 0.

Теорема 3.(достаточное условие строгого экстремума)

Пусть f непрерывна в точке x0 и дифференцируема на . Пусть меняет знак при переходе через точку x0. Тогда x0 - точка строгого экстремума. Доказательство:Пусть для определенности f' > 0 на U(x0 + 0). Тогда из формулы конечных приращений Лагранжа f(x) − f(x0) =f'(ξ)(x − x0) видно, что приращение функции f меняет знак с "-" на "+" при переходе через

точку x0.Следовательно, x0 - точка строгого максимума. Замечание: условия теоремы не являются необходимыми. Пример: Теорема 4.Пусть . Тогда

1. при четном n = 2k, x0 - точка строгого экстремума (строго минимума) при (при );

2. при нечетном n = 2k + 1, x0 - точка возрастания (точка убывания) при (при ).

Теорема 1 (условие выпуклости функций).

Пусть функция f имеет вторую производную f'' на (a,b). Тогда

1 условие 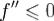на (a,b) необходимо и достатчно для выпуклости вверх функции f на (a,b);

2 если f'' < 0 на (a,b), то функция f строго выпукла вверх на (a,b).

Доказательство:

Достаточность: При a < α < x < β < b имеем, условие выпуклости вверх

а используя формулу конечных приращений Лагранжа

при f''(ξ) < 0),a < α < ξ < ζ < η < β < b.

Теорема 2 (необходимые условия точки перегиба).

Пусть x0 - точка перегиба функции и f'' непрерывна в x0. Тогда f''(x0) = 0.

Доказательство:от противного

Допустим, что и для определенности f''(x0) > 0. Тогда f''(x) > 0 в некоторой окрестности U(x0). Значит точка x0 находится внутри

интервала U(x) строгой выпуклости вниз и не может быть точкой перегиба.

Теорема 3 (достаточные условия точки перегиба).Пусть , а f'' меняет знак при переходе через точку x0.Тогда x0 - точка перегиба. Доказательства:сводится к проверке определения точки перегиба с помощью теоремы о достаточных условиях строгой выпуклости функции.

Теорема 4 (о расположении кривой относительно касательной).

1 Если f''(x0) > 0(f''(x0) < 0), то : кривая y = f(x) лежит строго выше

(строго ниже) касательной y = f(x0) +f'(x0)(x − x0) при .

2 Если 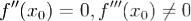, то : кривая y = f(x) переходит через

касательную, т.е. при x< x0 и 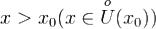лежит строго по разные стороны от касательной.