2.4. Теорема сложения вероятностей несовместных событий

Суммой А + В двух событий А и В называют событие, которое происходит, если происходит или событиеА , или событиеВ , или оба эти события. СуммойА +В двух несовместных событий А и В называют событие, которое происходит, если происходит или событиеА , или событиеВ.

Суммой А₁ + А₂ + … + А_n нескольких событий называют событие, которое происходит, если происходит хотя бы одно из событийА₁ ,А₂ , … ,А_n. СуммойА₁ +А₂ + … +А_n нескольких несовместных событий называют событие, которое происходит, если происходит или событиеА₁ , илиА₂ , …, илиА_n .

Теорема. Вероятность суммы нескольких несовместных событий равна сумме вероятностей этих событий:

Р(А₁ +А₂ + … +А_n ) =Р(А₁ ) +Р(А₂ ) + … +Р(А_n ) .

События называются единственно возможными , если появление в результате испытания одного и только одного из них является достоверным событием.

Полной группой называют совокупность единственно возможных событий испытания.

Теорема. Сумма вероятностей событийА₁ ,А₂ , … ,А_n , составляющих полную группу, равна единице:

Р(А₁ ) +Р(А₂ ) + … +Р(А_n ) = 1 .

2.5. Теорема умножения вероятностей независимых событий

Два события называют независимыми, если вероятность появления одного из них не зависит от появления или непоявления другого. Несколько событий называютпопарно независимыми , если каждые два из них независимы.

Произведением двух событий А и В называют событиеАВ , которое происходит, если совместно происходят и событиеА , и событиеВ .Произведением нескольких событий называют событие, которое происходит, если совместно происходят все эти события.

Теорема. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:

Р(АВ) =Р(А)∙Р(В).

Несколько событий называют независимыми в совокупности, если каждое из них и любой набор из части или всех остальных событий есть независимые события. Справедливо следующее утверждение: Вероятность произведения (совместного появления) нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

Р(А₁ А₂ …А_n) =Р(А₁ ) ∙Р(А₂ ) ∙ … ∙Р(А_n ) .

2.6. Серии независимых испытаний Формула Бернулли

Пусть проводится ряд одинаковых испытаний, в результате каждого из которых может появиться или не появиться событие А. Если на появление (или не появление) событияА в данном испытании не влияют результаты других испытаний, то такие испытания называют независимыми относительно событияА .

Будем считать, что вероятность появления события А в каждом испытании одна и та же и равнаp. Очевидно, что вероятность непоявления событияА в каждом испытании также постоянна и равнаq = 1 –p.

Вероятность события, состоящего в том, что в n независимых испытаниях событиеА произойдетk раз (и не произойдетn-k раз) находится по формуле

, (2.2)

или

. (2.3)

Эту формулу называют формулой Бернулли. Биномиальные коэффициенты учитывают то, что в последовательностиn испытаний появления и непоявления событияА могут чередоваться в разных комбинациях. По смыслу- это число сочетаний поk элементов, которые можно выбрать изn элементов. В формуле Бернуллидает число разных последовательностей поk испытаний (в которыхА происходит), которые можно выделить в серии изn испытаний. Числоравно вероятности того, что событиеА произойдет в каждом испытании определенной группы изk испытаний, и не произойдет вn-k остальных испытаниях.

Пример 2.2. На некотором участке 40% деревьев определенного вида поражено вредителем. Найти вероятность того, что из шести случайно выбранных на участке деревьев четыре окажутся пораженными вредителем.

Решение.По условию задачи вероятность того, что одно случайно выбранное на участке дерево окажется пораженным вредителем, равнаp = 0,4. Вероятность того, что оно не будет поражено вредителем, равнаq = 1-p =0,6. Случайно выбраны и затем исследованы на предмет пораженности вредителем шесть деревьев. Это значит, что проведено шесть независимых испытаний. Вероятность того, какие-то четыре дерева из этих шести окажутся пораженными, равна

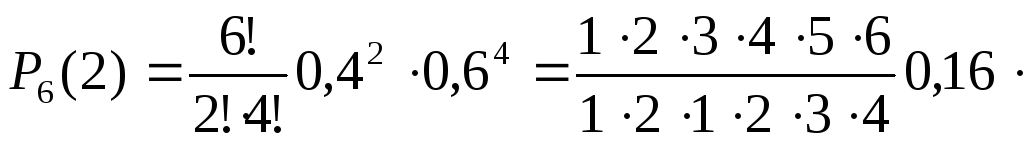0,1296 = 0,31.