
- •Методы оптимизации. Ответы на вопросы.
- •Конечномерные экстремальные задачи без ограничений.
- •Конечномерные экстремальные задачи с ограничениями.
- •Свойства выпуклых множеств.
- •Выпуклые оболочки.
- •Проекция точки на множество.
- •Отделимость выпуклых множеств.
- •Свойства выпуклых функций.
- •Критерии выпуклости функций.
- •Минимум выпуклой функции.
- •Функция Лагранжа и седловая точка.
- •Теорема Куна-Таккера.
- •Связь между основной и двойственной задачами.
- •Условия сходимости градиентных методов.
- •Условия сходимости метода Ньютона.
- •Условие сходимости метода штрафных функций.
- •Условие сходимости методов возможных направлений
- •Вариация функционала
- •Доказательство.
- •Простейшая задача вариационного исчисления.
- •Доказательство.
- •Уравнение Эйлера-Лагранжа
- •Условия Лежандра и Якоби
- •Доказательство.
- •Постановка вариационной задачи с подвижными границами.
- •Доказательство:
- •Задача Больца
- •Изопериметрическая задача.
- •Задача Лагранжа
- •Метод Ритца
- •Общая постановка задачи оптимального управления.
- •Достаточное условие существования решения задачи оптимального управления.
- •Принцип максимума л. С. Понтрягина. Необходимые условия.
- •Принцип Эйлера-Лагранжа и оптимальное управление
- •Необходимые условия в задаче теории оптимального управления
- •Принцип максимума Понтрягина для простейшей задачи оптимального управления
- •Задача линейного быстродействия.
- •Достаточные условия оптимальности в задаче линейного быстродействия.
- •Фундаментальная матрица и формула Коши.
- •Принцип Крейна.
-
Теорема Куна-Таккера.
Дополнительные
условия, сформулированные Куном-Таккером
в различных по постановкам теоремам
являются обобщением принципа Лагранжа.
Рассмотрим случай
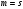 задачи
ВП. Тогда
задачи
ВП. Тогда
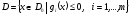 .
(1)
.
(1)
Опр.
1.
Множество (1) называется регулярным
(выполнение условия Слейтера), если
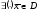 такая, что
такая, что
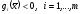 .
.
Замечание.
Для выполнения условия Слейтера
достаточно потребовать:
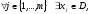 что
что
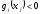 .
Тогда из выпуклости
.
Тогда из выпуклости
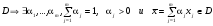 ,
а из выпуклости
,
а из выпуклости
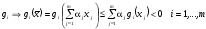 .
.
Теорема
1 (Куна-Таккера).
Пусть в задаче ВП
 ,
выполнено условие регулярности и
,
выполнено условие регулярности и
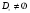 .
Тогда
.
Тогда
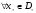
 вектор
вектор
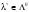 такой, что
такой, что
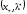 является седловой точкой функции
Лагранжа для этой задачи.
является седловой точкой функции
Лагранжа для этой задачи.
Доказательство
Рассмотрим
в
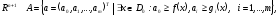
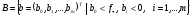 .
Покажем:
.
Покажем:
 .
Пусть
.
Пусть
 ,
что
,
что
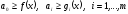 .
Если
.
Если
 .
Если
.
Если
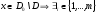 ,
что
,
что
 .
.
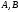 -
выпуклы!
-
выпуклы!
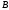 -
т.к. оно пересечение конечного числа
полупространств. Покажем для
-
т.к. оно пересечение конечного числа
полупространств. Покажем для
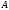 .
Пусть
.
Пусть
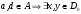 ,
что
,
что
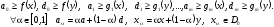
Из
выпуклости
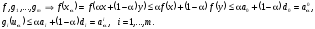
И
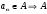 выпукло.
выпукло.
Из
(Т.1, п.2.4)
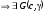 - гиперплоскость,
- гиперплоскость,
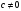 отделяющая
отделяющая
 .
Обозначим
.
Обозначим
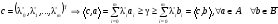 (2)
Покажем:
(2)
Покажем:
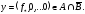 Действительно, пусть
Действительно, пусть
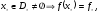
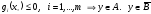 (очевидно)
(очевидно)
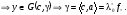 Тогда
Тогда
(2)
перепишется:
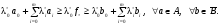 (3)Из (3) выведем:
(3)Из (3) выведем:
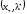 ,
где
,
где
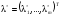 удовлетворяет условиям (Т.4.1.1) и является
Седловой точкой.
удовлетворяет условиям (Т.4.1.1) и является
Седловой точкой.
Пусть
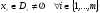 положим
положим
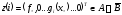 .
Из левой части (3) для
.
Из левой части (3) для
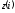 получаем
получаем
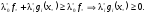 Из правой части (3)
Из правой части (3)
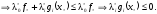 Значит
Значит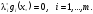 (4)
(4)
В
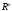 рассмотрим
рассмотрим
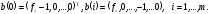
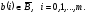 Подставляя
Подставляя
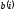 в правую часть (3), получим:
в правую часть (3), получим: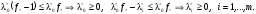 Покажем,
что
Покажем,
что
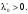 Пусть
Пусть
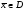 точка, фигурирующая в условиях Слейтера,
тогда
точка, фигурирующая в условиях Слейтера,
тогда
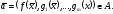 Для
Для
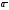 из левой части (3) находим
из левой части (3) находим
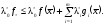 (5)
(5)
Предположим,
 Тогда, т.к.
Тогда, т.к.
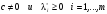 из условий Слейтера следует
из условий Слейтера следует
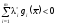 .
Это противоречит (5), т.е. значит
.
Это противоречит (5), т.е. значит
 Поделив
Поделив
 на
на
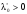 можно считать
можно считать
 Осталось показать, что
Осталось показать, что
 (6)
(6)
Пусть
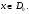 Для
Для
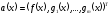 выполняется
выполняется
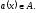 С учетом
С учетом
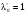 из левой части (3) для этой точки получим
из левой части (3) для этой точки получим
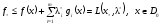 и в силу (4) получаем условие (6).
и в силу (4) получаем условие (6).
Замечание.
При
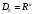 задача ВП является частным случаем
задачи 1 (П.3.1). Предположим, что в задаче
ВП
задача ВП является частным случаем
задачи 1 (П.3.1). Предположим, что в задаче
ВП
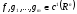 .
Тогда условие 1 в (Т.1., п.4.2) принимает вид
.
Тогда условие 1 в (Т.1., п.4.2) принимает вид
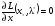 и из теоремы Куна-Таккера вытекает
теорема Кароша-Джона, в которой
и из теоремы Куна-Таккера вытекает
теорема Кароша-Джона, в которой
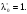 Обратно, если в задаче ВП некоторая
точка
Обратно, если в задаче ВП некоторая
точка
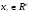 удовлетворяет условиям (Т.1, п.1.3) при
удовлетворяет условиям (Т.1, п.1.3) при
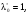 то по Т.,п.4.2 пара
то по Т.,п.4.2 пара
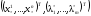 является седловой точкой функции
Лагранжа этой задачи и по Т.2, п.4.2 точка
является седловой точкой функции
Лагранжа этой задачи и по Т.2, п.4.2 точка
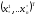 доставляет решение задаче ВП.
доставляет решение задаче ВП.
-
Связь между основной и двойственной задачами.
Пусть
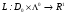 - функция Лагранжа для задачи ВП. Введем
в рассмотрение функцию
- функция Лагранжа для задачи ВП. Введем
в рассмотрение функцию
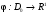 ,
,
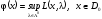
Тогда
 и при
и при
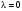 неравенство переходит в равенство.
Если
неравенство переходит в равенство.
Если
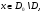 то либо
то либо
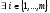 ,
что
,
что
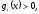 либо
либо
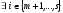 ,
что
,
что
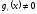 .
В любом случае
.
В любом случае
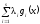 выбором
выбором
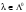 можно сделать сколь угодно большой,
поэтому
можно сделать сколь угодно большой,
поэтому
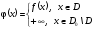 и
и
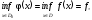 .
.
Поэтому исходная задача может быть записана в виде:
Задача
1.
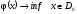 .
.
Поступим
аналогичным образом, поменяв роль
переменных и операций максимизации и
минимизации, т.е. введем наряду с функцией
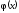 функцию
функцию
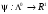 ,
определенную формулой
,
определенную формулой
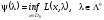 и
рассмотрим задачу.
и
рассмотрим задачу.
Задача
2.
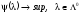 .
.
Опр.
1.
Задача 2 называется двойственной к
задаче 1, которая называется основной.
Переменные
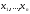 называются основными, а
называются основными, а
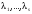 двойственными. В качестве примера
рассмотрим следующую задачу:
двойственными. В качестве примера
рассмотрим следующую задачу:
 ,
(1) где А – матрица размерности
,
(1) где А – матрица размерности
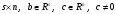 .
Она называется задачей линейного
программирования в канонической форме.
Для этой задачи
.
Она называется задачей линейного
программирования в канонической форме.
Для этой задачи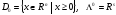 ,а
функция Лагранжа
,а
функция Лагранжа
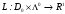 имеет вид:
имеет вид: .
.
Функция
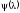 выписывается в явном виде
выписывается в явном виде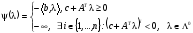
Отсюда
ясно, что точку
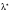 ,
на которой может достигаться верхняя
грань функции
,
на которой может достигаться верхняя
грань функции
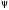 ,
достаточно искать во множестве
,
достаточно искать во множестве
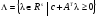 .
Двойственная задача к задаче (1)
формулируется следующим образом:
.
Двойственная задача к задаче (1)
формулируется следующим образом: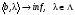 (2). Таким образом, двойственная задача
к задаче (1) тоже является задачей
линейного программирования. Можно
показать, что двойственная задача к
задаче (2) будет исходной задачей (1).
(2). Таким образом, двойственная задача
к задаче (1) тоже является задачей
линейного программирования. Можно
показать, что двойственная задача к
задаче (2) будет исходной задачей (1).
Замечание. В общем случае задача двойственная к двойственной не всегда совпадает с исходной.
Задачи
1 и 2 из предыдущего пункта тесно связаны
между собой. Обозначим
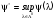 .
.
Теорема
1.
Имеет место неравенство
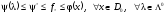 .
.
Доказательство
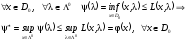
Переходя
в последнем неравенстве к нижней грани
по
 ,
получим искомое неравенство
,
получим искомое неравенство
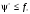 .
.
Замечание.
Существуют
задачи ВП, для которых
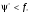 .
.
Теорема
2. Для
того, чтобы было выполнено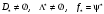 (1) необходимо и достаточно, чтобы функция
Лагранжа имела седловую точку на
множестве
(1) необходимо и достаточно, чтобы функция
Лагранжа имела седловую точку на
множестве
 .
Множество Седловых точек функции
Лагранжа совпадает с
.
Множество Седловых точек функции
Лагранжа совпадает с
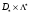 .
.
Доказательство
Необходимость.
Пусть выполнено (1). Покажем, что
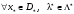 пара
пара
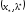 является седловой для функции Лагранжа
имеем
является седловой для функции Лагранжа
имеем
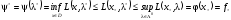 (2)
(2)
Т.к.
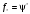 из (2) следует
из (2) следует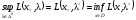 (3). Последнее равенство означает,
что
(3). Последнее равенство означает,
что
 .Таким
образом, пара
.Таким
образом, пара
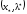 - седловая точка и множество
- седловая точка и множество
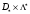 принадлежит множеству точек функции
Лагранжа.
принадлежит множеству точек функции
Лагранжа.
Достаточность.
Пусть
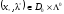 -
седловая точка функции Лагранжа. Тогда
-
седловая точка функции Лагранжа. Тогда
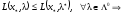
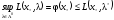 (4).
Аналогично, из неравенства
(4).
Аналогично, из неравенства

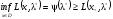 (5). Из (3) и (5) с учетом Т.1 получаем
(5). Из (3) и (5) с учетом Т.1 получаем
 .
.
Тогда
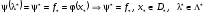 .
.
Отсюда
выводим, что множество седловых точек
функции Лагранжа принадлежит множеству
 .
.
Теоремы 1 и 2 в совокупности образуют теорему двойственности.
Замечание. Если задача линейного программирования имеет решение, то для нее существует седловая точка функции Лагранжа. Тогда по Т.2 двойственная задача имеет решение и значения целевых функций этих точек совпадают.
