
вышка. КР№3
.pdf
J |
|
(1) |
|
|
(x 2 y3 |
dx dy |
|
(2) |
|
(1) |
dydz |
||
|
x |
|
y |
|
y |
|
z |
||||||
T |
|
|
|
|
|
|
|||||||
+ |
(x 2 y3 ) |
|
|
(2) |
|
dzdx |
3 x 2 y2dx dy . |
||||||
|
z |
|
x |
||||||||||
|
|
|
|
|
D |
|
|
|
|||||
Последний интеграл есть двойной интеграл по кругу D Oxy, на который проектировался круг Т; D: x 2 y2 1. Перейдем к
полярным координатам: x=rcos , y=rsin , 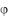 [0;2 ], r [0;1]. В итоге:
[0;2 ], r [0;1]. В итоге:
|
2 |
1 |
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
J |
3 d |
r2 cos2 r2 sin2 rdr |
3 cos2 |
sin2 d |
r5dr |
|
|
. |
||||||||||
8 |
||||||||||||||||||
|
0 |
0 |
|
|
|
|
|
0 |
|
|
|
0 |
|
|
||||
Пример 3. Найти поток П векторного поля |
|
(x 2; y2;z2 ) |
||||||||||||||||
F |
||||||||||||||||||
через |
полную поверхность |
Т пирамиды |
W: |
x |
2y |
3z |
6, |
|||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
0, y |
0, z |
0 |
|||
(рис. 2.19) в направлении внешней нормали к поверхности. |
|
|||||||||||||||||
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
3 |
y |
|
|
|
|
|
||||
|
|
x 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Рис. 2.19 |
|
|
|
|
|
|
|
||||||
Решение. Поток равен |
|
П |
|
x 2dydz y2dzdx |
z2dx dy . |
|||||||||||||
T
Применяя формулу Остроградского-Гаусса (2.24), сводим задачу к вычислению тройного интеграла по фигуре W -пирамиде:
П |
|
|
|
(x 2 ) |
|
( y2 ) |
|
|
|
|
(z2 ) |
|
dx dydz |
|
|||||||||||||||||
W |
|
|
x |
|
y |
|
|
|
z |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
x |
2 |
x |
|
|
2 y |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
|
3 |
|
|
|
|||||||||
2 |
(x y |
|
|
z)dx dydz |
|
|
2 dx |
|
|
dy |
|
|
|
(x |
y z)dz |
||||||||||||||||
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|||||
|
3 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6 |
2 |
|
|
|
8 |
|
|
4 |
|
|
|
5 |
x 2 |
|
14 |
|
|
|
|
|
|
8 |
y2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
dx |
4 |
|
x |
|
y |
|
|
x y |
|
|
|
|
dy |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
0 |
0 |
|
|
|
3 |
|
3 |
|
|
9 |
|
|
9 |
|
|
|
|
|
9 |
|
|
|
|||||||||
6 |
|
|
|
|
7 |
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
10 |
|
x |
x 2 |
|
x 3 dx |
|
20. |
|
|
|
|
|
|
|
|
|
||||||||||||||
0 |
|
6 |
108 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
51 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
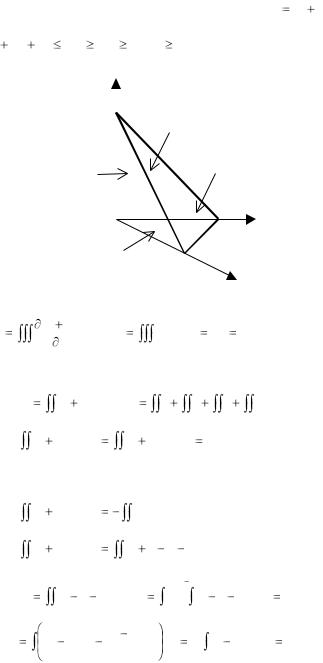
Пример 4. Найти поток П векторного поля F |
(x 3z)k |
че- |
|||||||||
рез |
полную |
|
|
поверхность |
|
T |
|
пирамиды |
W: |
|||
x |
2y 3z 6; x |
0; y 0 ; |
z 0 |
(рис. |
2.20), в |
направлении |
||||||
внешней нормали к поверхности. |
|
|
|
|
|
|
||||||
|
|
z |
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T3 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T4 |
|
|
|
|
|
|
T2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
3 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T1 |
|
6 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.20
Решение. Применим формулу Остроградского-Гаусса (2.24)
П |
(x 3z) |
dxdydz |
3dxdydz 3V 18 , где V – объем пи- |
|
|||
W |
z |
W |
|
|
|
||
рамиды. Сравним с решением непосредственного вычисления потока ( T1,T2 ,T3,T4 – грани пирамиды).
П |
(x 3z)dxdydz |
|
|
|
; |
|
T |
|
T1 |
T2 |
T3 |
T4 |
, |
|
|
|
|
|
|
|
(x |
3z)dxdy |
(x 3z)dxdy |
0; |
|
|
|
T3 |
|
T4 |
|
|
|
|
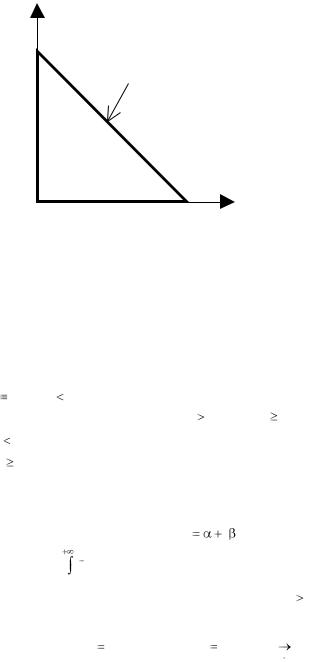
так как проекция граней T3, T4 на плоскость Oxy имеет нулевую площадь (рис. 2.21),
(x |
3z)dxdy |
|
xdxdy; |
|
|
|
|
|
||
T1 |
|
|
G |
|
|
|
|
|
|
|
(x |
3z)dxdy |
|
(x 6 |
x |
2 y)dxdy; |
|||||
T2 |
|
|
G |
|
|
|
|
|
|
|
|
|
3 |
6 |
2 y |
|
|
||||
П |
(6 x |
2 y)dxdy |
dy |
|
(6 x |
2 y)dx |
||||
G |
|
0 |
|
0 |
|
|
|
|||
3 |
2 y)2 |
|
(6 2 y)2 |
|
1 |
|
3 |
2 y)2 dy 18. |
||
(6 |
|
|
|
dy |
|
|
|
(6 |
||
2 |
|
2 |
|
|||||||
0 |
|
|
|
|
0 |
|
||||
|
|
|
|
|
52 |
|
|
|
|
|
y |
|
|
3 |
x+2y=6 |
|
|
|
|
|
G |
|
O |
6 |
x |
|
||
|
Рис. 2.21 |
|
3. ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
3.1. Оригинал и его изображения
|
|
Функция f (t) |
действительного переменного |
t называется |
||||||
оригиналом, если она удовлетворяет условиям: |
|
|
||||||||
1) |
|
f (t) |
0 при t |
0 ; |
|
|
|
|
||
2) |
существуют |
такие |
постоянные |
M 0 |
и |
S0 0 , что |
||||
|
|
f (t) |
|
MeS0 t |
для всех t; |
|
|
|
||
|
|
|
|
|
|
|||||
3) |
при t |
0 функция |
f (t) непрерывна или имеет конечное чис- |
|||||||
|
ло точек разрыва первого рода на каждом конечном интерва- |
|||||||||
|
ле оси Ot. |
|
|
|
|
|
|
|||
|
|
Изображением функции f (t) по Лапласу называется функ- |
||||||||
ция |
|
F( p) |
комплексного переменного |
p |
i , |
определяемая |
||||
равенством F ( p)  e pt f (t)dt . Если f (t) – оригинал, интеграл
e pt f (t)dt . Если f (t) – оригинал, интеграл
0
в правой части последнего равенства сходится при Re p 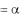 S0 .
S0 .
Тот факт, что F( p) |
является изображением оригинала |
f (t) , бу- |
|
. |
. |
дем обозначать так: |
F( p) L( f (t)) или F ( p) f (t), F ( p) |
f (t) . |
|
. |
|
|
53 |
|

Таблица 3.1 Изображение основных элементарных функций
f (t) при t 0 |
|
|
|
|
L( f (t)) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
t n |
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
pn |
1 |
|
|
|
|
|
|
|||
e t |
|
1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
sin |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p 2 |
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
cos t |
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
p 2 |
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
sh |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p 2 |
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
ch |
t |
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
p 2 |
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
t sin |
t |
|
|
|
|
|
|
2 p |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
( p2 |
2 )2 |
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||
t cos |
t |
|
|
|
|
p2 |
2 |
|
|
|
|
||||||
|
( p2 |
2 )2 |
|
|
|||||||||||||
|
|
|
|
|
|||||||||||||
3.2. Основные теоремы операционного исчисления
1. Теорема линейного изображения.
Для любых оригиналов f (t) и g(t) и любых чисел a, b L(af (t) bg(t)) aL( f (t)) bL(g(t)) .
Пусть всюду в дальнейшем L( f (t)) F( p) .
2. Теорема подобия (изменения масштаба). Для любого
постоянного C 0 L( f (Ct)) |
1 |
F |
p |
. |
|
|
|||
|
C |
|
C |
|
3. Теорема смещения. Для любого числа
: L(e t f (t)) F( p
t f (t)) F( p 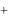 ) .
) .
4. Теорема о дифференцировании оригинала. Если функции f (t), f (t), , f (n) (t) являются оригиналами, то
54

|
L( f (t)) |
|
|
pF( p) |
f (0); |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
L( f (t)) |
|
|
p2 F ( p) |
|
pf (0) |
|
f (0); |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
L( f (n) (t)) |
|
pn F ( p) |
|
pn 1 f (0) |
pn |
2 f |
(0) |
f (n 1) (0). |
|||||||||||||||||||
|
5. Теорема о дифференцировании изображения. |
|
||||||||||||||||||||||||||
L(t n f (t)) |
( |
1)n F (n) ( p), |
|
n |
1,2, . |
|
|
|
|
|
|
|
|
|||||||||||||||
|
6. Теорема об интегрировании оригинала. |
|
|
|||||||||||||||||||||||||
|
t |
|
|
|
F ( p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
L f (s)ds |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0 |
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
7. Теорема об интегрировании изображения. |
|
|
|||||||||||||||||||||||||
L |
f (t) |
|
|
F ( y)dy |
(если интеграл сходится). |
|
|
|
||||||||||||||||||||
t |
|
|
|
|||||||||||||||||||||||||
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
8. Теорема запаздывания. L( f (t |
t0 )) |
e |
pt0 F ( p) |
, |
t0 0 . |
||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
9. Теорема об изображении свертки двух функций. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
L( f1 * f2 ) |
F1( p)F2 ( p) , где |
f1 * f2 |
|
|
f1(s) f2 (t |
s)ds |
|
– свертка |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
функций f1(t) и f2 (t) , |
F1( p) L( f1(t)), F2 ( p) L( f2 (t)) . |
|||||||||||||||||||||||||||
|
Пример 1. Найти изображения функции shat sin bt . |
|||||||||||||||||||||||||||
|
Решение. Известно, что |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
L(sin bt) |
|
|
b |
|
|
|
|
F( p); |
|
sh at |
|
1 |
|
(eat |
e at ) . Тогда |
|||||||||||||
p2 |
|
|
b2 |
|
2 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
shat sin bt |
|
1 |
|
e |
at |
sin bt |
|
1 |
e |
at |
sin bt . По теореме линейности |
|||||||||||||||||
2 |
|
|
|
2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
имеем L(sh at sin bt) |
|
1 |
L(eat sin bt |
|
1 |
|
L(e at sin bt) . В каждом из |
|||||||||||||||||||||
2 |
|
2 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
полученных слагаемых применим теорему смещения и получаем
|
1 |
F( p a) |
1 |
|
F( p a) |
|
1 |
|
|
b |
|
|
1 |
|
|
|
b |
|
.Это и |
2 |
2 |
|
2 |
|
( p |
a)2 |
b2 |
|
2 ( p |
a)2 |
b2 |
||||||||
есть искомое изображение. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Пример 2. Найти свертку функций t и e t |
и ее изображение. |
||||||||||||||||
|
|
|
|
|
t |
|
|
|
|
t |
|
|
|
|
|
|
t |
|
|
|
|
Решение. |
t * et |
set |
s ds |
|
set e |
s ds |
et |
se |
s ds . Вычис- |
||||||||
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
ляя интеграл, имеем tet |
|
et (1 |
te t |
e t ) . По теореме об изобра- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
55 |
|
|
|
|
|
|
|
|
|

жении свертки L(t * et ) L(t)L(et ) |
|
1 |
|
|
. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
p2 ( p 1) |
|
|
|
||||||
Пример 3. Найти L(te 2t |
sin t) . |
|
|
|
|
|
|
|
|
|
||||
Решение. Найдем F( p) |
L(sin t) |
1 |
|
|
. По теореме о |
|||||||||
|
|
|
|
|
||||||||||
|
p2 |
|
|
|||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
||||
дифференцировании изображения |
|
|
|
|
|
|
|
|
|
|||||
L(sin t t) F ( p) |
1 |
|
|
|
2 p |
G( p) . Наконец, по |
||||||||
|
|
|
|
|
|
|
|
|||||||
p2 1 |
|
( p2 |
1)2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||
теореме смещения L(e 2tt sin t) G( p |
2) |
|
|
|
2( p |
2) |
|
. |
||||||
|
|
|
|
|
|
|||||||||
|
(( p2 1)2 |
|
1)2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
3.3. Отыскание оригинала по изображению
При отыскании оригинала по изображению в простейших случаях используют таблицу изображений основных элементарных функций и теоремы разложения.
Вторая теорема разложения позволяет найти оригинал по известному изображению, являющемуся дробно-рациональной
функцией p : |
F( p) |
u( p) / v( p) , где u( p) и v( p) |
– многочлены |
|||
от p соответственно степени m и n, причем m n . Если разложе- |
||||||
ние |
v( p) |
на |
простейшие |
множители |
имеет |
вид |
v( p) ( p p )k1 ( p p )k2 ( p |
|
p )kr , k k |
2 |
|
k |
r |
n , |
то, |
|||||||||||||||||
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
r |
|
|
1 |
|
|
|
|
|
|
|||
как известно, |
F( p) |
может быть разложена на сумму элементар- |
|||||||||||||||||||||||
|
|
|
|
|
|
|
Ajs |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ных дробей вида |
|
|
|
|
|
|
; |
j |
1, r; |
s |
|
1, k j . Итак, |
|
||||||||||||
( p |
|
p j )k j |
s 1 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
r |
k j |
|
Ajs |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
F ( p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.1) |
||
j 1s 1 ( p p j )k j |
|
s 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Все коэффициенты могут быть найдены по формуле |
|
|
|||||||||||||||||||||||
Ajs |
1 |
|
|
|
lim |
|
d s |
1 |
[( p |
p j ) |
k |
j F ( p)] |
. |
|
|
|
(3.2) |
||||||||
(s |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1)! p |
p j dps |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Вместо этой формулы для определения коэффициентов A js
можно использовать элементарные приемы, применяемые в математическом анализе при интегрировании рациональных дробей.
56

Если все корни многочлена v( p) простые, разложение упрощает-
ся: v( p) ( p |
p1)(p |
p2 ) ( p |
|
|
pn ); |
|
|
( p j |
|
|
|
pk |
при j |
k) ; |
|||||||
|
|
|
n |
|
|
Aj |
|
|
|
|
|
|
|
|
|
u( p j ) |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F ( p) |
|
|
|
|
|
|
, где |
|
Aj |
|
|
|
|
|
|
. |
(3.3) |
|||
|
j 1 p |
p j |
|
|
|
v ( p j ) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
После отыскания тем или иным способом разложения F( p) |
|||||||||||||||||||||
на простейшие дроби оригинал |
|
|
f (t) находится так: |
|
|||||||||||||||||
а) в случае кратных корней знаменателя |
|
|
|
|
|||||||||||||||||
|
|
|
r |
|
k j |
|
|
t k j |
|
s |
|
|
p |
j |
t |
|
|
|
|
||
|
|
f (t) |
|
|
|
Ajs |
|
|
|
|
|
|
e |
|
|
; |
|
|
(3.4) |
||
|
|
|
|
|
(k j |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
j |
1 s |
1 |
|
|
|
s) ! |
|
|
|
|
|
|
|
|||||
б) в случае простых корней знаменателя v( p) |
|
||||||||||||||||||||
|
|
|
f (t) |
r |
|
|
u( p |
j |
) |
e |
p j t |
. |
|
|
|
(3.5) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
j |
1 v ( p j ) |
|
|
|
|
|
|
|
|
||||||
Пример |
1. Найти |
|
оригинал |
|
|
|
f (t) , |
|
|
если |
известно, что |
||||||||||
F ( p) L( f (t)) |
|
|
|
p |
1 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||
|
p( p |
1)( p |
2)( p 3) |
|
|
|
|
|
|
|
|
||||||||||
Решение. |
У изображения |
|
F( p) |
|
|
в данном случае все корни |
|||||||||||||||
знаменателя – действительные и простые. Поэтому лучше всего воспользоваться формулой (3.5). Имеем
u( p) |
p |
1; |
v( p) |
p( p |
1)( p |
2)( p |
3) |
|
|
|
|
p 4 |
6 p3 |
11 p 2 |
6 p; v ( p) 4 p3 |
18 p 2 |
22 p 6. |
||||||
Корни |
|
|
|
|
|
|
|
|
|
|
|
v( p) : p1 |
0; |
p2 1; |
p3 |
2; p4 |
3; |
u( p1 ) |
|
1 |
; |
||
v ( p1 ) |
6 |
||||||||||
|
|
|
|
|
|
|
|
||||
u( p2 ) |
1; |
|
u( p3 ) |
|
|
3 |
|
; |
|
u( p4 ) |
|
||||||||
v ( p2 ) |
|
v ( p3 ) |
|
2 |
|
|
v ( p4 ) |
||||||||||||
Отсюда |
|
|
|
по |
|
|
формуле |
||||||||||||
f (t) |
|
1 |
|
e |
t |
|
3 |
e |
2t |
|
2 |
e |
3t |
. |
|
||||
6 |
|
|
2 |
|
3 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Пример |
|
2. |
Найти |
оригинал |
|||||||||||||||
F( p) |
|
|
|
|
|
|
|
p |
|
|
|
. |
|
|
|
|
|||
|
|
|
|
|
|
||||||||||||||
|
( p 1)3 ( p 2)2 |
|
|
|
|
||||||||||||||
32 .
(3.5) находим f (t) :
f (t) по его изображению
Решение. Разложение F( p) |
на простейшие дроби имеет вид |
||||||||||
F( p) |
A11 |
|
A12 |
|
|
A13 |
|
A21 |
|
A22 |
. (3.6) |
( p 1)3 |
|
( p 1)2 |
p 1 ( p 2)2 |
|
p 2 |
||||||
|
|
|
|
||||||||
|
|
57 |
|
|
|
|
|
||||
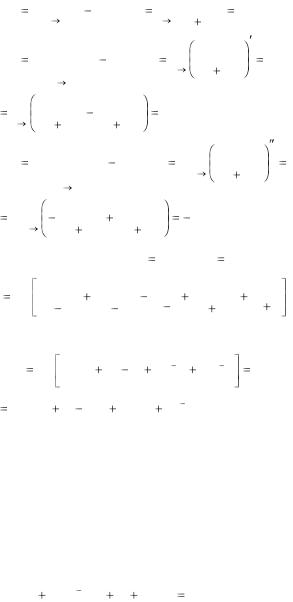
Находим коэффициенты Aij |
|
|
по формуле (3.2) |
|
||||||||||||||||||||||||||||||||||||||||||||
|
A |
1 |
|
|
lim (( p |
1)3 F ( p)) |
lim |
|
|
|
|
|
p |
|
|
|
|
1 |
; |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
11 |
|
|
0! p |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
p 1 ( p |
2)2 9 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
A |
1 |
|
lim |
|
d |
(( p 1)3 F ( p)) |
|
|
lim |
|
|
|
|
|
p |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
12 |
|
|
1! |
|
|
|
|
dp |
|
|
|
|
|
|
|
|
|
|
|
p |
1 |
|
|
( p |
|
2)2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
p |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
lim |
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
2 p |
|
|
|
1 |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( p 2)3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
p 1 ( p 2)2 |
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
A |
1 |
lim |
d 2 |
(( p |
1)3 F ( p)) |
1 |
lim |
|
|
|
p |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
13 |
|
|
2! |
|
|
|
dp2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 p 1 |
|
( p |
2)2 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
p |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
lim |
|
|
|
4 |
|
|
|
|
|
6 p |
|
|
|
|
|
|
|
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
( p 2)3 |
|
( p 2)4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
2 p 1 |
|
|
|
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Аналогично получим A |
|
2 |
; |
|
|
A |
|
1 |
|
|
. Следовательно, |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
27 |
|
|
|
|
22 |
27 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
F ( p) |
1 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
. Отсюда |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
27 |
|
|
( p |
1)3 |
|
|
|
( p |
1)2 |
|
|
p |
1 |
|
|
( p |
|
2)2 |
|
|
|
|
p 2 |
|||||||||||||||||||||||||
по таблице изображений и теоремам смещения и линейности изображения имеем
f (t) |
|
1 3 |
t |
2 |
e |
t |
te |
t |
e |
t |
2te |
2t |
2 |
0 |
e |
2t |
||||
|
27 |
|
2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
(3t 2 |
|
2t 2)et |
|
1 |
|
(2t 1)e 2t . |
|
|
|
|
||||||||
54 |
|
|
27 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Заметим, что коэффициенты разложения (3.6) можно найти и таким способом, который применялся в математическом анализе при интегрировании рациональных дробей.
3.4. Решение дифференциальных уравнений и систем дифференциальных уравнений операционным методом
Пусть дано линейное дифференциальное уравнение (ЛДУ) n- го порядка с постоянными коэффициентами
y(n) (t) a y(n 1) |
(t) a y(t) f (t) , |
|
1 |
|
n |
правая часть которого |
f (t) является оригиналом. Тогда и реше- |
|
ние y(t) этого уравнения, удовлетворяющее начальным условиям
58

y(0) y |
0 |
, y (0) |
y |
0 |
, |
, y(n |
1) (0) y (n |
1) (то есть решение |
|
|
|
|
|
0 |
|
||
задачи Коши для данного ЛДУ), тоже будет оригиналом. |
||||||||
Обозначим |
изображение |
искомого |
решения y(t) через |
|||||
S( p) , то есть S( p) |
|
|
L( y(t)) . Используя теорему о дифференци- |
|||||
ровании оригинала и свойство линейности, находим изображение левой части исходного ЛДУ и приравниваем его к L( f (t)) . В
итоге вместо ЛДУ с начальными условиями получается так называемое изображающее уравнение, которое является линейным алгебраическим уравнением относительно новой неизвестной
функции S( p) |
L( y(t)) . Решая изображающее уравнение, нахо- |
||||||||||||||||||||||||||||||||||||||||||||||
дим |
S( p) . Определяя затем по |
S( p) оригинал y(t) , |
мы тем са- |
||||||||||||||||||||||||||||||||||||||||||||
мым найдем искомое решение |
|
y(t) |
задачи Коши. |
|
Аналогично |
||||||||||||||||||||||||||||||||||||||||||
решаются и системы ЛДУ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Пример 1. |
|
|
Решить |
ЛДУ |
|
|
y'' (t) |
2y (t) |
3y(t) |
|
e3t , |
если |
|||||||||||||||||||||||||||||||||
y(0) |
y (0) |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Решение. Обозначим L( y(t)) |
S( p) . По теореме о диффе- |
|||||||||||||||||||||||||||||||||||||||||||
ренцировании |
|
|
оригинала |
|
|
|
|
имеем |
|
|
|
L( y (t)) |
|
|
pS( p) y0 ; |
||||||||||||||||||||||||||||||||
L( y (t)) |
p2S( p) |
|
py |
y |
0 |
|
|
p2S( p) . |
|
|
Тогда |
|
|
изображающее |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
уравнение |
|
таково: |
p2 S ( p) |
|
|
2 pS( p) |
3S ( p) |
1 |
|
|
|
. |
|
|
Отсюда |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
p |
3 |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
S( p) |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
. |
Восстановим теперь |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
( p |
|
3)( p2 |
2 p |
3) |
|
|
( p |
|
1)( p |
3)2 |
||||||||||||||||||||||||||||||||||||
оригинал |
y(t) |
. |
|
|
S( p) . Разложим вначале дробь S ( p) |
на про- |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
стейшие дроби: |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
A |
|
|
|
B |
|
C |
. Ищем |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
( p 1)( p |
3)2 |
|
|
|
( p |
|
|
3)2 |
|
|
( p |
3) |
|
|
p |
1 |
|||||||||||||||||||||||||||||
A, B, C: 1 A( p 1) B( p 3)(p |
|
|
1) C( p 3)2 . Полагая |
p |
1, |
||||||||||||||||||||||||||||||||||||||||||
получаем 1 |
16C , |
то есть C |
1 16 ; |
полагая |
p |
|
3, p |
|
|
0 , |
|
получа- |
|||||||||||||||||||||||||||||||||||
ем |
1 A |
|
3B |
|
9C , |
откуда |
|
|
|
B |
1 |
|
( A |
|
9C |
1) |
|
|
|
|
1 |
, |
|
A |
|
1 |
. |
||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
16 |
|
4 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
S ( p) |
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
1 |
1 |
|
|
|
|
|
|
y(t) |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
4 ( p 3)2 |
|
|
|
16 ( p |
3) |
|
|
16 ( p |
1) . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
1 |
te3t |
|
1 |
e3t |
1 |
|
e t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
4 |
|
16 |
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Решение поставленной задачи Коши найдено.
59
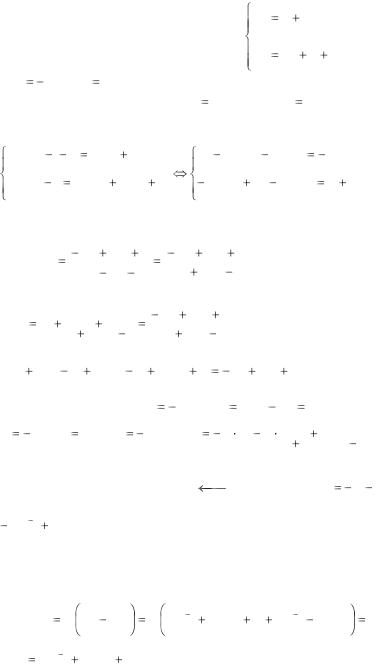
|
dx |
|
x |
2 y; |
|
|
|
||
|
dt |
|||
Пример 2. Решить систему ЛДУ |
|
|
если |
|
dy |
|
|
||
|
|
2x |
y 1, |
|
|
|
|
||
|
dt |
|
||
|
|
|
|
|
x(0) 1, y(0) 5 . |
|
|
|
|
Решение. Обозначим L(x(0)) T ( p), L( y(t)) |
S( p) и най- |
|||
дем изображения левой и правой частей каждого из уравнений системы.
pT ( p) ( 1) T ( p) 2S ( p) |
( p 1)T ( p) 2S ( p) |
1; |
|
|
|
|
|||||||||||||||||||||||||||||||||||
pS( p) 5 2T ( p) S ( p) |
1 |
|
|
2T ( p) ( p 1)S ( p) S |
|
1 |
. |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
||||
|
Из последней линейной алгебраической системы уравнений |
||||||||||||||||||||||||||||||||||||||||
находим неизвестную T ( p) |
|
(например, по формулам Крамера) |
|||||||||||||||||||||||||||||||||||||||
|
T ( p) |
|
|
|
|
p2 |
|
11 p |
2 |
|
|
|
|
|
|
|
p2 |
11 p |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
p(( p 1)2 |
4) |
|
|
|
|
|
p( p |
1)( p |
3) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
Разложим T ( p) |
на |
|
|
простейшие |
рациональные |
дроби: |
||||||||||||||||||||||||||||||||||
T ( p) |
|
A |
|
|
|
B |
|
|
C |
|
|
|
|
|
|
p2 |
11 p |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
p |
|
p |
1 |
|
p 3 |
|
|
|
p( p |
1)( p |
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Для |
определения |
чисел |
A, |
|
B, C получаем равенство |
|||||||||||||||||||||||||||||||||||
A( p 1)(p 3) Bp( p 3) |
Cp( p 1) |
|
|
|
p2 |
|
11p 2 . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
Подставляя в обе части равенства вместо p поочередно числа |
||||||||||||||||||||||||||||||||||||||||
–1; |
3 |
|
и |
0, |
|
имеем |
4B |
|
|
|
|
10, |
12C |
26, |
|
3A |
2 . Отсюда |
||||||||||||||||||||||||
B |
5 |
|
; C |
13 |
; A |
2 |
|
; T ( p) |
|
2 1 5 |
1 |
|
13 |
|
1 |
. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
2 |
|
|
|
|
|
|
6 |
|
|
3 |
|
|
|
|
|
|
|
|
3 p 2 p 1 6 p 3 |
|||||||||||||||||||||
Пользуясь таблицей изображений и свойством линейности изо-
бражения, |
найдем |
оригинал |
|
x(t) |
|
|
T ( p) . |
Итак, x(t) |
2 |
|
||||||||||||||||||||||
|
. |
|
|
|||||||||||||||||||||||||||||
3 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
e |
t |
13 |
|
e3t , одна из искомых функций найдена. |
Функцию |
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
2 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y(t) |
можно найти аналогично x(t) , предварительно определив ее |
|||||||||||||||||||||||||||||||
изображение S ( p) . Но в данном случае y(t) |
можно найти проще, |
|||||||||||||||||||||||||||||||
выражая из первого уравнения исходной системы ЛДУ |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
y(t) |
|
|
1 dx |
x(t) |
|
1 |
|
5 |
e t |
|
13 |
e3t |
2 |
|
5 |
e t |
13 |
e3t |
|
|
|||||||||
|
|
|
|
2 |
|
dt |
|
|
2 |
2 |
|
2 |
3 |
|
2 |
6 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
5 |
e |
t |
|
13 |
e3t |
1 |
. |
Задача решена. |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
2 |
|
|
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|
|
|
|
