
Контрольная работа для Ольги Лысой
.pdf
Задание 7. Найти dy функций.
|
|
|
|
|
|
|
|
dx |
||
а) |
y = |
|
|
|
|
+ |
|
|
; б) y = xarcsin x ; в) x4 - 6x2 y2 + 9 y4 - 5x2 +15 y2 -100 = 0 ; |
|
|
x arcsin |
x |
1- x |
|||||||
x = t 2 + 2, |
|
|
|
|
|
|||||
г) |
1 |
|
|
|
|
|
|
|
|
|
y = |
|
t3 |
-1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
3 |
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|||||
а) |
y = |
|
|
|
|
+ |
|
|
; |
|
|
x arcsin |
x |
1- x |
|||||||
Для вычисления производной используем свойство производной суммы
( f + g )¢ = f ¢ + g¢ , производной произведение ( f × g )¢ = f ¢× g + f × g¢ и производной сложной функции ( f (g (x)))¢ = f ¢(g (x))× g¢(x). Так же производную табличной функции
(xr )¢ = rxr −1 и (arcsin x)¢ = |
|
|
1 |
|
. Тогда получим |
|
|
|
|
||
|
- x2 |
||||
1 |
|
|
|||
|
dx |
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
( |
|
|
|
|
|
|
|
|
|
) |
|
|
( |
|
|
) |
|
|
|
( |
|
) |
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
) |
||||||||||||||
|
dy |
= |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
¢ |
= |
|
|
|
|
|
|
|
|
|
|
|
¢ + |
|
|
|
|
|
¢ = |
|
|
|
¢ ×arcsin |
|
+ |
|
× |
|
|
|
|
|
|
|
¢ + |
|||||||||||||||||||||||
|
|
|
|
|
|
|
x arcsin |
x |
1- x |
|
|
x arcsin |
x |
|
|
1- x |
|
|
x |
x |
x |
|
|
arcsin |
x |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
1 |
|
|
- x)¢ |
|
|
1 |
1 |
−1 ×arcsin |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
×( |
|
|
)¢ - |
|
|
|
1 |
|
|
arcsin |
|
|
|
x |
|
|
|
|||||||||||||||||||||||||||
+ |
×(1- x) |
|
−1 ×(1 |
= |
× x |
|
|
x |
+ |
x |
× |
|
|
|
|
|
|
|
|
|
x |
|
|
|
= |
|
+ |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1- ( |
x ) |
2 1- x |
2 x |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
arcsin |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
arcsin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
+ |
|
|
|
|
× |
|
|
|
- |
|
|
|
|
= |
|
|
x |
+ |
|
|
|
- |
|
|
|
|
= |
|
|
x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 x × 1- x 2 1- x |
|
|
|
2 x |
|
|
|
|
2 1- x 2 1- x |
|
|
|
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
б) |
y = xarcsin x ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Применяем операцию логарифмирования, получаем ln y = ln xarcsin x , |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ln y = arcsin x ×ln x . Дифференцируем это равенство по x , учитывая что y = y (x). Тогда получим
(ln y )¢ = (arcsin x ×ln x)¢ , |
|
1 |
× |
dy |
= (arcsin x)¢ ×ln x + arcsin x ×(ln x)¢ , |
|||||||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
y dx |
|
|
|
|
|
|
|
|
|
|||
|
dy |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
ln x |
|
|
arcsin x |
|||
|
|
= y × |
|
|
|
×ln x |
+ arcsin x × |
|
|
= xarcsin x × |
|
|
|
+ |
|
. |
||||
dx |
|
|
|
x |
|
|
|
x |
||||||||||||
1- x2 |
1- x2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
в) x4 - 6x2 y2 + 9 y4 - 5x2 +15 y2 -100 = 0 ; |
|
|
|
|
|
|
|
|
|
||||
Производная неявной функции F (x, y ) = 0 вычисляется по формуле |
dy |
= - |
Fx′ |
, где |
|||||||||
|
F ¢ |
||||||||||||
|
|
|
|
|
|
|
|
|
|
dx |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
Fx′ и Fy′ частные производные по x и y соответственно. |
|
|
|
|
|
|
|||||||
Вычислим частные производные: |
|
|
|
|
|
|
|
|
|
||||
Fx¢ = (x4 - 6x2 y2 + 9 y4 - 5x2 +15 y2 -100)¢ |
= 4x4−1 - 6 × 2x2−1 × y2 - 5 × 2x2−1 = 4x3 -12xy2 -10x , |
|
|
||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
Fy¢ = (x4 - 6x2 y2 + 9 y4 - 5x2 +15 y2 -100)¢ |
= -6 × x2 ×2 y2−1 + 9 × 4 y4−1 +15 ×2 y2−1 = -12x2 y + 36 y3 + 30 y . |
||||||||||||
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
dy |
|
4x3 -12xy2 -10x |
|
2x (2x2 - 6 y2 - 5) |
x |
|
|
|||||
Тогда получим |
|
= - |
|
= |
|
= |
|
. |
|
|
|||
dx |
-12x2 y + 36 y3 + 30 y |
6 y (2x2 - 6 y2 - 5) |
3y |
|
|
||||||||
x = t 2 + 2, |
|||
г) |
1 |
|
|
y = |
|
t3 |
-1. |
|
|||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = x (t ), |
вычисляется по |
|
Производная функции заданной параметрически |
y = y (t ), |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
формуле |
dy |
= |
yt′ |
|
. Тогда |
|
|
|
|
|
|
|
||||||||||
|
|
x¢ |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
= |
(t2 + 2)¢ |
|
= |
2t 2−1 |
= |
2t |
= |
2 |
. |
|
|
|||||||||
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||
|
dx |
1 |
|
|
3 |
|
¢ |
|
×3t3−1 |
|
t 2 t |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
t |
|
-1 |
|
|
3 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

Задание 8. Исследовать функцию и построить ее график.
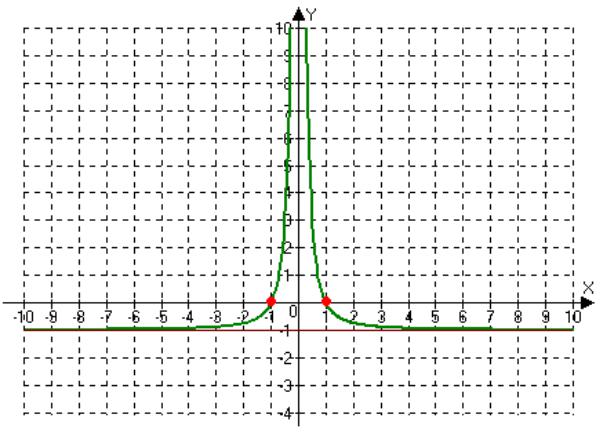
y= 1- x2 . x2
Решение.
1) Область определение. Так как знаменатель дроби не равен 0, то x2 ¹ 0 , т.е. x ¹ 0 . Тогда D (y ) = (-¥; 0)È (0; +¥).
Прямая x = 0 могут быть вертикальными асимптотами. Вычислим односторонние пределы в этих точках:
В точке x = 0 ,
lim |
1− x2 |
= |
1−(−0)2 |
|
= +∞ и lim |
1− x2 |
= |
1−(+0)2 |
= +∞. |
|||||||
|
|
(−0)2 |
|
(+0)2 |
||||||||||||
x→−0 x2 |
|
|
|
|
x→+0 x2 |
|
||||||||||
Прямая x = 0 вертикальная асимптота. |
||||||||||||||||
2) Четность не четность функции. |
|
|
||||||||||||||
y (−x) = |
1−(−x)2 |
= |
1− x2 |
= y (x). |
|
|
||||||||||
|
|
|
|
|
||||||||||||
|
|
|
(−x)2 |
x2 |
|
|
|
|
|
|||||||
Функция четная. Функция не периодическая. |
||||||||||||||||
3) Пересечение с осями координат: |
|
|
||||||||||||||
с осью Ox : y = |
1− x2 |
= 0 , |
x = −1 и x =1 . Точка (-1; 0) и (1; 0) . |
|||||||||||||
|
||||||||||||||||
|
|
|
|
|
|
x2 |
|
|
|
1 |
|
|
2 |
|
||
с осью Oy : так как x = 0 |
не входит в область определения, точек пересечения с |
|||||||||||||||
осью Oy нет.
4) Монотонность функции и точки экстремума.
|
1- x2 ¢ |
|
1 |
¢ |
1 ¢ |
|
|
|
|
|
|
|
|
2 1 |
|
|
|
2 |
|
|||||||||||||||||||||||||
y¢ = |
|
|
|
|
|
|
|
|
= |
|
|
-1 |
= |
|
|
|
|
- (1)¢ |
= -2 × x |
− − - 0 |
= - |
|
|
|
|
|||||||||||||||||||
|
|
x |
2 |
|
|
|
|
2 |
|
|
2 |
|
|
x |
3 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Критических точек нет. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Составим таблицу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
(-¥; 0) |
|
|
0 |
|
|
|
|
(0; +¥) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′ |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+¥). Точек экстремума нет. |
|||||||||||||||||||||||||||||
|
Функция |
|
возрастает |
(-¥; 0) |
, убывает (0; |
|||||||||||||||||||||||||||||||||||||||
5) Выпуклость и вогнутость функции, точки перегиба. |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 ¢ |
|
|
|
|
|
|
3 1 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
y¢¢ = -2 × |
|
|
|
|
|
= -2 ×(-3)× x− − |
= |
|
|
> 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
3 |
|
x |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Так как вторая производная функции на всей области определения больше 0, то |
||||||||||||||||||||||||||||||||||||||||||||
функция на всей области вогнута |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
6) Найдем асимптоты графика функции при x → ±∞ . Асимптоты вида y = kx +b , |
||||||||||||||||||||||||||||||||||||||||||||
где k = lim |
y |
|
|
и b = lim |
(y - kx). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
x→∞ x |
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
1- x |
2 |
|
|
|
|
1- x |
2 |
|
|
|
|
|
|
x |
|
|
|
|
-1 |
|
|
|
|
|
-1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
k = lim |
|
|
|
|
|
|
|
|
: x |
= lim |
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
= 0 и |
|||||||||||||
|
|
x |
2 |
|
|
x |
3 |
|
|
|
|
|
|
x |
3 |
|
|
|
x |
|
||||||||||||||||||||||||
|
x→∞ |
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
x→∞ |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
1- x |
2 |
|
|
1- x |
2 |
|
x |
|
|
|
|
-1 |
1 |
|
|
||||
|
|
|
2 |
|
||||||||||||||||
|
|
|
|
|
|
x |
|
|
= 0 -1 = -1 . |
|||||||||||
b = lim |
|
|
|
- 0 × x |
= lim |
|
|
|
= lim |
|
|
|
|
|
|
= lim |
|
|
-1 |
|
x |
2 |
|
x |
2 |
|
|
|
|
x |
2 |
|
|
2 |
|||||||
x→∞ |
|
|
|
x→∞ |
|
|
x→∞ |
|
|
|
|
x→∞ x |
|
|
|
|||||
Получили асимптоту y = −1. 7) Построим график
