
Начертательная геометрия. Часть 2
.pdf
Министерство образования Республики Беларусь БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Инженерная графика строительного профиля»
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
Т |
|
|
|
|
|
|
|
|
Н |
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
й |
|
|
|
|
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ |
|
|||||||
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
Конспект лекц |
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
В 2 частях |
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
Часть 2 |
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
МЕТРИЧЕСКИЕ ЗАДАЧИ. |
|
|
|||
|
|
|
|
и |
|
|
|
|
|
|
|
ОДНОКАРТИННЫЕ ИЗОБРАЖЕНИЯ |
|
|
|||||
|
|
|
з |
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
п |
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
М и н с к Б Н Т У
2 0 1 1
УДК 515.18(075.8) ББК 22.151.3я7
Н 36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Авторы: |
|
|
|
|
|
||
|
|
|
|
Л.С. Корытко – лекции 9–10, |
|
|
|
У |
|||||
|
|
|
|
Ю.И. Садовский |
– лекция 11, |
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
М.К. Протасова – лекции 12, |
|
|
|
|
|||||
|
|
|
|
И.М. Шуберт – лекции 13, 16–17, |
|
Т |
|||||||
|
|
|
|
М.В. Кравченко – лекции 14–15, 18, |
|
||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
В.В. Тарасов – лекции 9, 15 |
|
|
|
|
|||||
|
|
|
|
Е.А. Телеш – графическое оформление |
Н |
|
|||||||
|
|
|
|
Под редакцией В.В. Тарасова |
|
|
|||||||
|
|
|
|
Б |
|
|
|||||||
|
|
|
|
|
Рецензенты: |
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
В.А. Столяр, П.В. Зелёный |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
й |
|
|
|
|
Н 36 |
|
Начертательная геометрия: конспект |
лекций |
|
|
|
|
||||||
|
|
|
: в 2 ч. / Л.С. Корытко [и др.]; под ред. |
||||||||||
|
В.В. Тарасова. – Минск: БНТУ, 2011. – Ч. 2: Метр ческ е задачи. Однокартинные изображе- |
||||||||||||
|
ния. – 118 с. |
|
|
р |
|
|
|
|
|
||||
|
|
ISBN 978-985-525-535-3 (Ч.2). |
|
|
|
|
|
||||||
|
|
часть 1 «Метод Монжа. |
Позиционные задачи», |
|
|
|
|
||||||
|
|
Настоящий конспект лекций аз аб тан коллективом авторов кафедры «Инженерная |
|||||||||||
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
графика строительного профиля» Бел усск го национального технического университета и |
||||||||||||
|
предназначен для студен ов с р ельных специальностей. |
|
|
|
|
||||||||
|
|
Конспект состоит двух час ей: |
|
|
|
|
|
|
|
||||
|
|
часть 2 «Метр ческ е задачи. Однокартинные изображения». |
|
|
|
||||||||
|
|
Рассмотрены основные теоретические вопросы курса начертательной геометрии в соот- |
|||||||||||
|
ветствии с многолетней практ кой работы кафедры и увязкой с методикой проведения прак- |
||||||||||||
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
тических |
анят й, решены многие типовые задачи, вызывающие у студентов наибольшие |
|||||||||||
|
трудн сти. |
|
из |
|
|
|
|
|
|
|
|
||
|
|
Часть 1: Мет д Монжа. Позиционные задачи, авторы: Ю.И. Садовский, М.Н. Петрович, |
|||||||||||
|
п |
|
|
|
|
|
|
|
|
|
|
||
|
В. В. Тарас вз, Е.А. Телеш, издана в БНТУ в 2010 г. |
|
|
УДК 515.18(075.8) |
|||||||||
е |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
ББК 22.151.3я7 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
ISBN 978-985-525-535-3 (Ч.2) |
© БНТУ, 2011 |
ISBN 978-985-525-317-5 |
|
ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
Точки в пространстве обозначаются прописными буквами латинского алфавита A, B, C или цифрами 1, 2, 3 …
|
Произвольные линии в пространстве – строчными буквами латинского ал- |
|||||||||||
фавита a, b, c … |
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Прямые, параллельные плоскостям проекций: |
|
|
|
||||||||
|
горизонтали – h; |
|
|
|
|
|
|
|
Т |
|||
|
фронтали – f; |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
профильные прямые – p. |
|
|
|
|
|
Н |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
Плоскости общего положения, поверхности обозначаются заглавными |
|||||||||||
буквами греческого алфавита Ψ, Ω, Σ … |
|
|
|
Б |
|
|
||||||
|
|
|
|
|
|
|||||||
|
Плоскости проекций – буквой греческого алфавита Π с добавлением ниж- |
|||||||||||
него индекса 1, 2, 3 … |
|
|
|
|
|
й |
|
|
||||
|
Основные плоскости проекций: |
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||
|
горизонтальная – Π1; |
|
|
и |
|
|
|
|||||
|
фронтальная – Π2; |
|
|
|
|
|
|
|||||
|
профильная – Π3. |
|
|
р |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
Проекции точек, прямых и плоскостей на чертеже обозначаются теми же |
|||||||||||
|
|
|
|
|
о |
|
|
|
|
|
|
|
буквами, что и в пространстве, с добавлением подстрочного индекса 1, 2, 3, со- |
||||||||||||
ответствующего плоскости пр екций, на кото ой они получены. |
|
|
||||||||||
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
Обозначение основных пераций: |
|
|
|
|
|
|
|||||
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
совпадение отмечае ся знаком ≡ ; |
|
|
|
|
|
|
|||||
|
з |
|
|
|
|
|
|
|
|
|
||
|
о |
|
|
|
|
; |
|
|
|
|
||
|
взаимная принадлежность – знаком |
|
|
|
|
|||||||
|
пересечение |
тмечается знаком ∩; |
|
|
|
|
|
|
||||
е |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
результат остроения (логическое следствие) – знаком . |
|
|
|||||||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
3
Лекция 9
СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ И ИХ ПРИМЕНЕНИЕ К РЕШЕНИЮ ЗАДАЧ
|
Общие понятия. Способ замены плоскостей проекций |
У |
||||||||
|
|
|
9.1. Общие понятия |
|
|
|||||
|
|
|
|
Т |
||||||
|
|
|
|
|
|
|
|
|
||
|
Решение многих пространственных задач (позиционных и метрических) на |
|||||||||
эпюре часто усложняется из-за того, что заданные геометрические объекты |
||||||||||
|
|
|
|
|
|
|
|
Н |
|
|
(оригиналы) расположены произвольно относительно плоскостей проекций и, |
||||||||||
следовательно, проецируются на эти плоскости в искаженном виде. Задание на |
||||||||||
|
|
|
|
|
|
|
|
Б |
|
|
эпюре прямых и плоскостей частного положения значительно упрощает реше- |
||||||||||
ние задач и делает его выполнимым при помощи простейших графических по- |
||||||||||
строений. Например, проекции отрезка, расположенного наклонно ко всем |
||||||||||
|
|
|
|
|
|
|
й |
|
|
|
плоскостям проекций, не дают непосредственно его натуральную величину и |
||||||||||
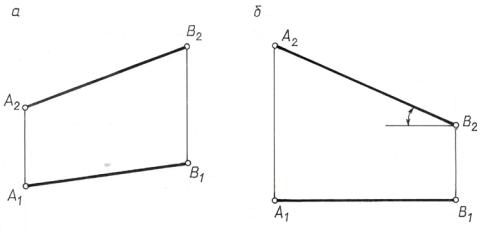
величину углов наклона его к плоскостям проекций (рис. 9.1, а). |
|
|
||||||||
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
||
|
|
и |
|
|
|
|
|
|
|
|
|
трезок |
|
|
Рис. 9.1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
На рис 9.1, б |
|
расположен параллельно фронтальной плоскости |
|||||||
проекций, эт му |
н проецируется на эту плоскость без искажения, т. е. |
|||||||||
ленных |
|
|
|
|
|
|
|
|
|
|
|А2В2| = |АВо|. |
|
|
|
|
|
|
|
|
|
|
Р |
По данному чертежу определяется также и угол наклона прямой АВ к го- |
|||||||||
ризо тальнойпплоскости проекций АВ^П1. При таком положении отрезка АВ го про кции можно считать удобно расположенными для решения постав-
задач.
Если на эпюре изображена плоская фигура общего положения (рис. 9.2, а), то без специальных построений нельзя сказать, какой угол она образует с плоскостью проекций, например, с П1. Между тем, если плоскость фронтально проецирующая (рис. 9.2, б), то наклон ее фронтальной проекции (фронтальная проекция треугольника) к оси проекций Х непосредственно дает величину угла, образованного плоскостью треугольника АВС с плоскостью П1.
4
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
Рис. 9.2 |
|
Б |
Т |
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
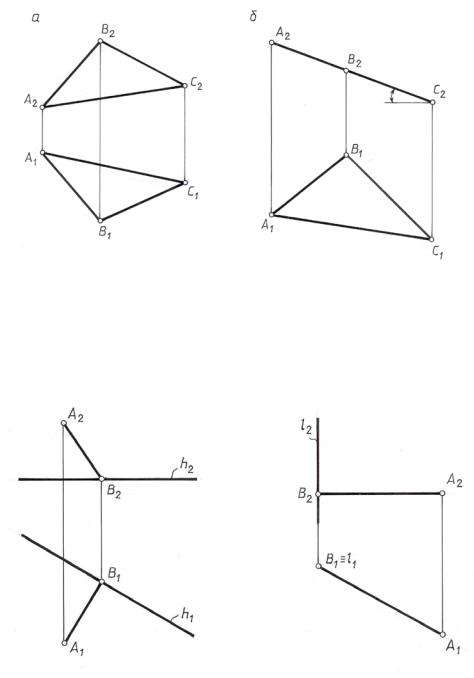
Для построения перпендикуляра из точки А(А1, А2) к горизонтальной пря- |
|||||||||||||
мой h(h |
, |
h |
) достаточно провести горизонтальную проекцию прямой А В |
h |
|||||||||
1 |
|
2 |
|
|
|
|
|
|
|
Н |
1 |
1┴ 1 |
|
(рис. 9.3), по линии связи найти точку В2 |
|
й |
|
|
|
||||||||
и соединить ее с точкой А2. |
|
|
|||||||||||
|
|
|
|
|
|
|
и |
|
|
|
|
||
|
|
|
|
|
|
р |
|
|
|
|
|
||
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
з |
Рис. 9.3 |
|
|
|
Рис. 9.4 |
|
|
|
|
|
Если |
орямая l(l1, l2) – горизонтально проецирующая (рис. 9.4), то легко не |
||||||||||||
только остроить перпендикуляр АВ (А1В1, А2В2) из точки А к прямой l(l1, l2), но и |
|||||||||||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
опредплить натуральную величину расстояния |АВ|=|А1В1| от точки до прямой. Возникает вопрос, как же следует поступить в том случае, если заданные
фигуры неудобно расположены относительно плоскостей проекций и затрудняют решение какой-либо задачи. В таких случаях прибегают к преобразованию проекций, т. е. замене исходных проекций изображаемой фигуры новыми (частного положения) с таким расчетом, чтобы последние позволили проще решать поставленную задачу.
В начертательной геометрии в качестве основных применяются следующие способы преобразования проекций:
5
1)способ замены плоскостей проекций;
2)способ плоскопараллельного перемещения;
3)способ вращения.
Основными задачами преобразования комплексного чертежа являются следующие:
1)преобразование прямой общего положения в прямую уровня;
2)преобразование прямой общего положения в проецирующую прямуюУ;
3)преобразование плоскости общего положения в проецирующую плос-
кость;
4)преобразование плоскости общего положения в плоскость уровняТ.Сущность способа состоит в том, что положение изображаемойНфигуры в
|
|
|
|
|
|
|
|
|
|
|
Б |
|
пространстве остается неизменным, а исходная система плоскостей проекций, |
||||||||||||
относительно которой задана фигура, заменяется новой. |
||||||||||||
|
При выборе новой плоскости проекций должен быть выполнен основной |
|||||||||||
принцип ортогонального проецирования (метода Монжа) – взаимной перпен- |
||||||||||||
|
|
|
|
П2 |
|
|
|
и |
|
|
||
дикулярности плоскостей проекций, т. е. новую плоскость проекций необходи- |
||||||||||||
мо обязательно располагать перпенд кулярно |
|
из основных исходных |
||||||||||
плоскостей проекций. |
|
|
|
р |
одной |
|
||||||
|
Пусть задана система плоскостей п оекц й П1 |
и П2 (в дальнейшем будем |
||||||||||
обозначать сокращенно П |
|
о |
|
|
|
|
||||||
). Сп |
еци уем точку А на эти плоскости и найдем |
|||||||||||
|
|
|
|
|
т |
|
|
|
|
|
||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
ее проекции А2 |
и А1 (рис. 9.5). |
|
|
|
|
|
|
|||||
|
|
|
|
и |
|
|
|
|
|
|||
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
п |
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
Рис .9.5
6
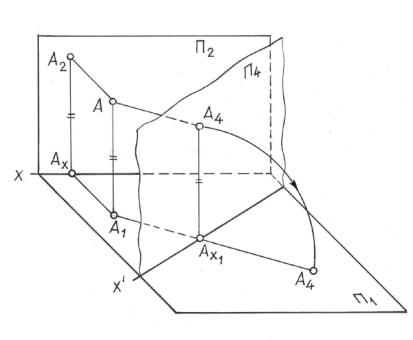
Предположим, что при решении какой-либо задачи целесообразно заменить плоскость П2 другой фронтальной плоскостью П4, перпендикулярной к плоскости П1. Линия пересечения плоскостей проекций П1 и П4 называется новой осью проекций и обозначается Х΄. Построим ортогональные проекции точ-
ки А в системе П4 . Так как плоскость П1 осталась прежней, то и проекция точ- |
|
П |
|
1 |
|
ки А на эту плоскость не изменит своего положения. |
|
Для получения новой фронтальной проекции точки на плоскость П4 опус- |
|
|
Т |
каем перпендикуляр из точки А на плоскость П4. Основание А4 этого перпенди- |
|
куляра определяет искомую фронтальную проекцию точки А. |
|
Установим, какая связь существует между проекциями А(А1, А2) и АУ(А1, А4) |
|
одной и той же точки в обеих системах. |
|
Горизонтальная проекция у них общая и так как расстояние точки А от |
|
плоскости П1 не изменилось, то |АА1| = |А2Аx| = |А4Аx΄|, т. е. расстояние новой |
||||||||||||||
фронтальной проекции до новой оси равно расстоянию заменяемой проекции |
||||||||||||||
до предыдущей оси. |
|
|
|
|
|
|
|
|
Н |
|||||
Чтобы перейти к эпюру, повернем плоскость П4 вокруг оси Х΄ и совместим с |
||||||||||||||
плоскостью П1. Тогда и новая фронтальная проекцияБА4 совместится с плоско- |
||||||||||||||
стью П1 |
и при этом окажется на одном перпендикуляре к осиХ1΄ с проекцией А1. |
|||||||||||||
На рис. 9.6 |
показаны те построен я, которые надо произвести на эпюре. |
|||||||||||||
Чтобы от проекций (А1, А2) точки А |
|
|
йП |
|||||||||||
в с стеме |
2 перейти к проекциям A1, А4) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П1 |
|
|
|
|
|
|
П4 |
|
|
|
|
и |
|||
той же точки в системе |
, не бх димо п овести новую ось проекций Х΄, ко- |
|||||||||||||
торая определяет |
|
П1 |
|
|
р |
|
|
|||||||
|
|
|
|
г риз нтально-проецирующей плоскости П4, за- |
||||||||||
тем из горизонтальной проекцочки А1 опустить перпендикуляр на новую |
||||||||||||||
ось Х΄. |
На построенном перпендикуляре отложить (от новой оси) отрезок |
|||||||||||||
Аx А4 |
|
|
|
|
|
|
т |
|
|
|
|
|
||
= АxА2. Полученная так м образом точка А4 является проекцией точки А |
||||||||||||||
на плоскость П4. |
|
положение |
|
|
|
|
|
|
||||||
Замена г ри |
|
нтальной плоскости П1 новой плоскостью П4 и построение |
||||||||||||
новых |
|
з |
|
|
|
|
П |
2 осуществляется аналогично рассмот- |
||||||
р екций т чки |
А в системе |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
П4 |
|
|
|
р нному случаюос той лишь разницей, что теперь остается без изменения фрон- |
||||||||||||||
тальная |
ро кция точки, а для нахождения новой горизонтальной проекции А5 |
|||||||||||||
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
точки А н обходимо из фронтальной проекции точки А2 опустить перпендику- |
||||||||||||||
ляр на новую ось Х΄и отложить на нем от точки пересечения с осью Х΄ отрезок |
||||||||||||||
е |
|
|
|
|
|
|
|
|
|
|
|
|
||
А5Аx΄, равный расстоянию старой горизонтальной проекции от старой оси А1Ах |
||||||||||||||
(рис. 9.7). |
|
|
|
|
|
|
|
|
|
|
|
|
||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
Т |
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
Рис 9.6 |
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
п |
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
Рис. 9.7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рассмотренные примеры позволяют установить следующее общее правило: для того чтобы построить проекцию точки в новой системе плоскостей проекций, необходимо из неизменяемой проекции точки опустить перпендикуляр на новую ось проекций и отложить на нем от новой оси до новой проекции расстояние, равное расстоянию от заменяемой проекции до предыдущей оси.
8

9.2.1. Замена двух плоскостей проекций
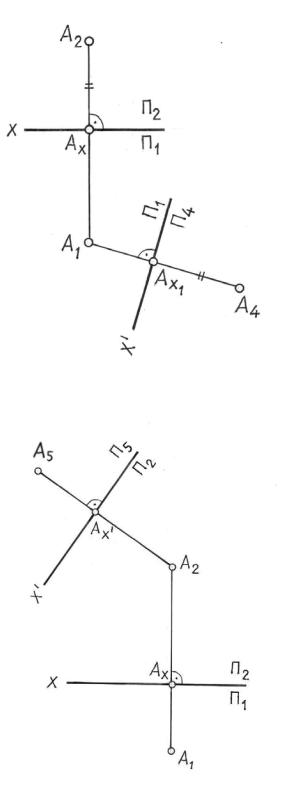
Некоторые задачи не могут быть решены заменой только одной плоскости проекций. Так, при определении действительной величины какой-либо геометрической фигуры или для получения более полного (наглядного) ее изображе-
ния замены одной плоскости проекций бывает недостаточно. |
|
У |
|||||||||||
|
На рис. 9.8 показан пример замены двух плоскостей проекций. Проекция |
||||||||||||
заданной точки А на плоскость П4 построена известным способом (см. рис. 9.6). |
|||||||||||||
Для построения проекции точки А5 |
на плоскость П5 из точки А4 |
опущен перпен- |
|||||||||||
дикуляр на новую |
|
|
|
|
|
|
|
|
Т |
||||
|
ось Х΄΄ и на этом перпендикуляре отложен отрезок |
||||||||||||
А2А5 = АХ΄А1. |
|
|
|
|
|
|
|
|
Н |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
и |
о |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
з |
т |
Рис. 9.8 |
|
|
|
|
||||
|
|
о |
|
а тем, чтобы не происходило накладывания новых про- |
|||||||||
|
Следует следить |
||||||||||||
екций на старые. |
|
|
|
|
|
|
|
|
|
|
|||
|
п |
|
|
|
|
|
|
|
|
|
|
||
е |
|
9.2.2. Основные задачи, решаемые способом замены |
|
||||||||||
Р |
|
|
|
|
|
плоскостей проекций |
|
|
|
||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
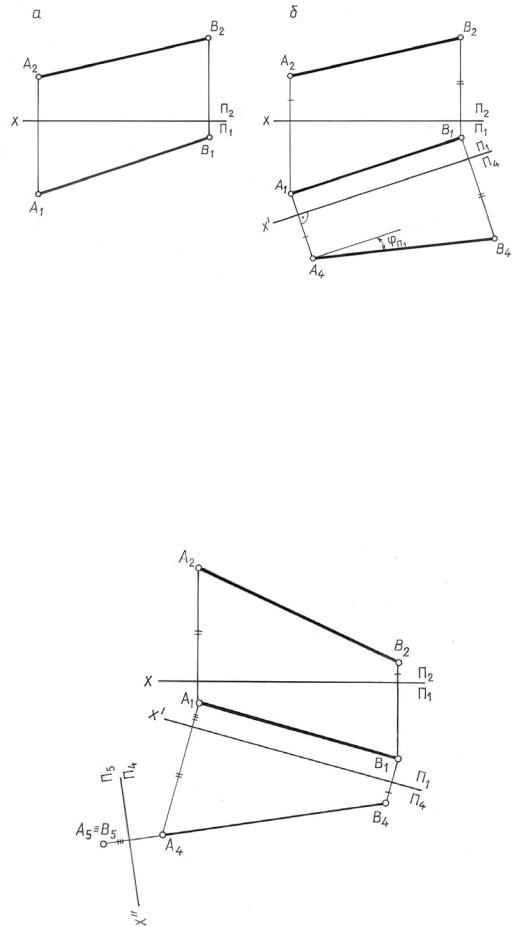
Задача 9.1. Преобразовать эпюр, изображенный на рис. 9.9, а, так, чтобы прямая общ го положения оказалась параллельной одной из плоскостей проекций новой системы.
Для решения задачи необходимо расположить новую плоскость проекций параллельно заданному отрезку (П ║АВ). Тогда на эту плоскость проекций отрезок проецируется без изменений.
9
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
Т |
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|
|
|
|
|
|
|
|
Рис. 9.9 |
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Решение этой задачи показано на рис. 9.9, б. Параллельно А1В1 проведена |
||||||||||||
|
|
|
|
|
|
|
|
|
|
прямой |
|
|
|
ось Х΄, и в системе плоскостей проекций |
П1 |
построена новая фронтальная |
|||||||||||
|
|
|
|
|
|
|
|
|
П4 |
|
|
|
|
проекция отрезка А4В4. Очевидно, что |
|А4В4| = |АВ| и угол φ, образованный |
||||||||||||
проекцией А4В4 |
с осью Х΄, равен углу наклона |
|
АВ к плоскости П1. |
||||||||||
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
Задача 9.2. Преобразовать эпюр, |
зоб аженный на рис. 9.10, так, чтобы |
|||||||||||
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
отрезок АВ прямой линии общего положенияиоказался перпендикулярным од- |
|||||||||||||
ной из плоскостей проекций. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 9.10
10
