
- •Миноры и алгебраические дополнения. Теорема Лапласа
- •12. Определение ранга матрицы методом окаймляющих миноров.
- •17.Выражение скалярного произведения через координаты( перемножаемых векторов)
- •26. Вывод канонического уравнения эллипса.
- •27. Вывод канонического уравнения параболы.
- •28.Гиперболические поверхности
- •31.Свойства пределов функции
- •33.Числовая последовательность. Предепредел последовательности.
- •36.Бесконечно малые величины и их св-ва
- •46. Достататочное условие существования экстремума.
- •49. Формула Телора
- •51. Производная суммы и частного.
- •56. Необходимое условие существования точек экстремума
- •57. Представление в виде формулы Тейлора основных элементарных функций
46. Достататочное условие существования экстремума.
Пусть функция y = f(x) непрерывна на всем интервале (a, b), дифференцируема на (a, b), кроме, быть может, числа x0(a,b), причем точка (x0, f(x0)) является критической точкой графика функции f. Тогда, если при переходе через x0 производная меняет знак с плюса на минус (с минуса на плюс), то f'(x0) – максимум (минимум) функции f.
Доказательство.
Пусть при переходе
через x0 производная функции f меняет
знак с плюса на минус. Рассмотрим x = x0
+ Δx(a,b) число . Если Δx > 0, то, воспользовавшись
теоремой Лагранжа, имеем f(x)-
f(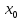 )=f’’(ζ)(x-x0)<0
где ζ
)=f’’(ζ)(x-x0)<0
где ζ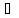 (x0,x)
т.е.f(x)<f(x0)
, если Δx < 0, то f(x0)-f(x)=f’’(ζ)(x0-x)>0,
где ζ
(x0,x)
т.е.f(x)<f(x0)
, если Δx < 0, то f(x0)-f(x)=f’’(ζ)(x0-x)>0,
где ζ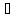 (x0,x),т.е.
f(x0)>f(x)
(x0,x),т.е.
f(x0)>f(x)
Доказано, что значение f(x0) – максимум функции f. Аналогично доказывается, что если при переходе через x0 производная меняет знак с минуса на плюс, то f(x0) – минимум функции f.
Теорема доказана.
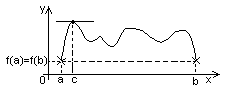
47. Теорема Роля: если функция f(x) непрерывна на заданном промежутке [a,b] деффер. на интервале (a,b) f(a)=f(b) то существует точка с из интервала (a,b), такая, что f’(c)=0.
48.
Правило Лопиталя представляет
собой метод вычисления пределов, имеющих
неопределенность
типа ![]() или
или![]() .
Пустьa является
некоторым конечным действительным
числом или равно бесконечности.
.
Пустьa является
некоторым конечным действительным
числом или равно бесконечности.
Если
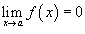 и
и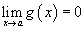 ,
то
,
то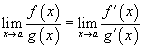 ;
;Если
 и
и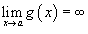 ,
то аналогично
,
то аналогично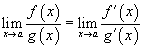 .
.
49. Формула Телора
Тейлора формула, формула
![]()
изображающая функцию f (x), имеющую n-ю производную f (n)(a) в точке х = а, в виде суммы многочлена степени n, расположенного по степеням х—а, и остаточного члена Rn (x), являющегося в окрестности точки а бесконечно малой более высокого порядка, чем (x—a) n [то есть Rn (x) = an (x)(x—a) n, где an (x) ® 0 при х ® а]. Если в интервале между а и х существует (n + 1)-я производная, то Rn (x)можно представить в видах:
![]()
51. Производная суммы и частного.
Производная произведения функций.
Пусть u(x) и u(x) -
дифференцируемые функции. Тогда
произведение функций u(x)v(x) также
дифференцируемо
![]()
Производная частного функций.
Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле
![]()
|
52. Теорема Коши |
|
Если
функции f (х)
и
Доказательство. Рассмотрим функцию
F(х) = [f(х)-f(а)] –
Легко
проверить, что эта функция удовлетворяет
теореме Ролля (аналогично тому, как
это было сделано в предыдущей теореме).
Следовательно, существует точка сÎ (a,
b.)
такая, что Отсюда получаем утверждение теоремы. Замечание.
Равенства
54. Теорема Лагранжа. Если функция f(x) непрерывна на [a,b] и дефференцирована на (a,b), то сущест. т. с(a,b), такая, что: f(b)-f(a)=f’(c)(b-a). Доказательство: применим т.Коши, взяв только g(x)=x, тогда g’(x)=10.
|
55. Необходимое условие существования точки перегиба:
если функция f(x),
дважды дифференцируемая в некоторой
окрестности точки x0, имеет в x0 точку
перегиба, то
![]() .
.
Достаточное условие
существования точки перегиба: если
функция f(x) в некоторой окрестности
точки x k раз непрерывно дифференцируема,
причем k нечётно и
![]() ,
и
,
и![]() при
при![]() ,
а
,
а![]() ,
то функция f(x) имеет в x0 точку перегиба.
,
то функция f(x) имеет в x0 точку перегиба.

