1. Матрица. Их виды. Линейные операции над матрицами.

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Обычно матрицы представляются двумерными (прямоугольными) таблицами. Квадратной называют матрицу, количество строк в которой равно количеству столбцов. Треугольная матрица — квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю. Диагональная матрица — квадратная матрица, все недиагональные элементы которой равны нулю. Обра́тная ма́трица — такая матрица A-1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E: Нулева́я ма́трица — это матрица, размера mxn, все элементы которой равны нулю. Единичная, Обратная Перестановочная, Симметричная. Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен b_ij = λa_ij. Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен c_ij = a_ij + b_ij Вычитание матриц A − B определяется аналогично сложению, это операция нахождения матрицы C, элементы которой c_ij = a_ij – b_ij

Умножение матриц. Транспонирование матриц.

Транспонирование матриц

Транспонирование матриц – переход от матрицы  А  к матрице, в которой строки и столбцы поменялись местами с сохранением порядка.

Свойства транспонированной матрицы:

1. (A^T)^T=A

2. Линейность: (A+B)^T = A^T+B^T

3. Умножение на число: (xA)^T = x*(A^T)

4. (A*B)^T = B^T*A^T

Умножение матриц

.

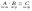Свойства умножения

1. АB != BA

2. 0A = A0 = 0

3. ABC = A(BC)

4. (A+B)C = AC + BC

2. Свойства Определителей

Св-ва: 1)Определитель не измениться, если его строки заменить столбцами и наоборот; 2) При перестановке 2-х парал рядов опред меняет знак на противоположный; 3)Определитель, имеющ два одинаковых ряда=0; 4)Общий множитель элементов какого-то ряда опред, можно вынести за знак опред; 5)если все элем ряда пропорц соотв элем парал ряда, то такой опред=0; 6)если все элем строки(столбца) определителя=0, то опред=0; 7) если элем определителя представ собой суммы двух слогаемых, то опред может быть разложен на сумму двух соотв определителей; 8)Определитель не изменится, если к элем одного ряда прибавить соотв элементы парал ряда, умноженного на число; 9)для разлож опред обычно выбирают тот ряд, где есть нулевые элементы, т.к. соотв им слаг будут=0; 10)сумма произведений элементов какого-либо ряда определителя на алг. дополнение параллельного ряда соотв элементов равно 0;

3.Миноры, алгебраические дополнения. Теорем о разложении определителя по элементам ряда

Миноры и алгебраические дополнения. Теорема Лапласа

Минором Мij квадратной матрицы n-го порядка для элемента аij называется определитель (n-1)-ого порядка, полученный с данного вычёркиванием i-ой строки и j-ого столбца.

Алгебраическое дополнение элемента определителяопределитель

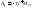где - минор

элемента.

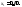
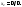
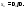
Теорема Лапласа. В данной квадратной матрице А(n x n ) вычеркнем k строк (1kn). Тогда равно сумме произведений всевозможных миновров к-того порядка из данных строк на их алгебраические дополнения: . То же для столбцов. Теорема удобна для матриц с большим кол-вом нулей.

4.Определители n-го порядка. Их свойства и методы вычисления.

Определителем n-го порядка называется число, равное алгебраической сумме всевозможных произведений элементов взятых по одному и только одному из каждой строки и каждого столбца.

Знак каждого слагаемого определяется числом инверсий в перестановках составленных из первых и вторых индексов сомножителей : если оно четное «+», нечетное «-».

Инверсия - когда большее число стоит перед меньшим.

Св-ва определителей:

1. В определителе строки и столбцы равнозначны.

2. Если все Эл-ты в строке или столбце = 0, то определитель =0.

3. Общий множитель строки или столбца можно выносить.

4. Если в определителе переставить местами 2 строки, то знак определителя изменится на противоположный.

5. Если в определителе 2 одинаковых строки/столбца, то определитель =0.

6. Если в определителе 2 строки пропорциональны, то определитель =0.

7. Определитель можно разложить на сумму.

8. Если в определителе некоторая строка/столбец является линейной комбинацией другой строки-столбца, то определитель =0.

9. Если к Эл-ам некоторой строки добавить соотв. Эл-ты другой строки умноженные на число не равное 0, то определитель не изменится.

Минор- определитель полученный из определителя n-го порядка вычеркиванием К каких-то строк и К столбцов.

Теорема Лапласа.

Определитель n-го порядка равен сумме произведений Эл-ов некоторой строки/столбца на их алгебраические дополнения.

Алгебраическое дополнение – A_ij=(-1)^i+jM_ij

Определитель треугольного вида равен произведению Эл-ов главной диагонали.

6. . Обратная матрица. Достаточное условие существования обратной матрицы. Определим операцию деления матриц как операцию, обратную умножению.Опр. Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:

XA = AX = E,где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратной к матрице А и обозначается А^-1.Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.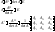

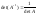
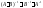
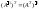
Для того чтобы матрица имела обратную достаточно того, чтобы она была невырождена.

7. «Матричная форма заииси системы линейных алгебраических уравнений»

Линейной системой mуравнений сn неизвестными, называется система вида:

(1) , гдеa_ij, h_i (i=1,m; j=1,n) – числа.

Заметим, что a_ij - коэффициент при неизвестном x_j в i-ом уравнении системы, h_i – свободный член в i-ом уравнении системы (1). Матрица A = составленная из коэффициентов при неизвестном сист. (1) – называетсяматрицей, или основной матрицей системы, а матрица =, которая получается из матрицы А приписыванием свободных членов, называется расширенной матрицей истемы (1).

Для того, чтобы записать систему (1) в матричной форме, наряду с матрицей системы А рассмотрим следующие матрицы:

X= 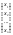;H = 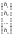; , т.к. матрица А согласованна с матрицей Х, то можно найти произведение А*Х=Н. Элементами полученной матрицы-столбца, являются левые части уравнения системы (1). На основании определения равенства матриц, систему (1) можно записать в виде матричного уравнения;

А*Х=Н (2) – такая запись называется матричной.

8. «Матричный метод для решения не вырожденных систем»

Матричный метод решения систем линейных уравнений.

Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.

Метод удобен для решения систем невысокого порядка.

Метод основан на применении свойств умножения матриц.

Пусть дана система уравнений:

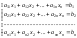
Составим матрицы: A= ;B = ;X = .

Систему уравнений можно записать:

AX = B.

Сделаем следующее преобразование: A^-1AX = A^-1B,

т.к. А^-1А = Е, то ЕХ = А^-1В

Х = А^-1В

Для применения данного метода необходимо находить обратную матрицу, что может быть связано с вычислительными трудностями при решении систем высокого порядка.

9.Формулы Крамера.

Система линейных уравнений:

Определители: Решение:

10. Ранг матрицы. Методы его вычисления.

Ответ: Рангом матрицы называется наибольший из порядков миноров матрицы , отличных от нуля. Ранг нулевой матрицы считается равным нулю. Ранг невырожденной квадратной матрицы порядка равен, так как ее определитель является минором порядка и у невырожденной матрицы отличен от нуля.

Рассмотрим прямоугольную матрицу. Выделим в этой матрице k произвольных строк и k произвольных столбцов (k≤n, k≤m). Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы. Так, у матрицы с тремя строками и пятью столбцами возможны миноры первого, второго и третьего порядка. Рангом матрицы А (обозначается r(A)) называется наибольший порядок минора этой матрицы, отличного от нуля. Если все элементы матрицы равны нулю, то ранг такой матрицы принимают равным нулю.

Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы. Ранг матрицы не изменится от следующих преобразований, называемых элементарными преобразованиями матрицы: - замены строк столбцами, а столбцов соответствующими строками; - перестановки строк матрицы; - вычеркивания строки, все элементы которой равны нулю; - умножения строки на число, отличное от нуля; - прибавления к элементам строки соответствующих элементов другой строки, умноженной на одно и то же число. Сама матрица при элементарных преобразованиях меняется, но ранг матрицы не изменится.

Свойства:

Свойство 1. При транспонировании матрицы её ранг не меняется.

Свойство 2. Ранг матрицы не меняется при перестановке её столбцов (строк).

Свойство 3. Ранг матрицы не меняется при умножении всех элементов её столбца (строки) на отличное от нуля число.

Свойство 4. Ранг матрицы не изменится, если к одному из её столбцов (строк) прибавить другой столбец (строку), умножив его (её) на некоторое число.

Свойство 5. Ранг матрицы не изменится, если удалить из неё столбец (строку), состоящий из одних нулей.

Свойство 6. Ранг матрицы не изменится, если удалить из неё столбец (строку), являющийся линейной комбинацией других столбцов (строк).

11. Элементарными преобразованиями матрицы называют:

     1) умножение какой-нибудь строки (столбца) на отличное от нуля число;

     2) прибавление к какой-нибудь строке (столбцу) другой ее строки (столбца), умноженной на произвольное число;

     3) перестановку местами любых двух строк (столбцов).