
- •К у р с о в а я р а б о т а
- •«Выбор эргономически обоснованных параметров мобильного транспортного средства на основе оптимизированной модели его колебательной системы»
- •Содержание
- •2.2. Вывод обобщенных перемещений………………………………………........................6
- •Введение
- •1. Постановка задачи
- •2. Вывод системы формул для расчёта оптимизационной модели автомобиля
- •2.1. Расчётная схема многоопорной машины с указанием варьируемых параметров
- •2.2. Выбор обобщенных перемещений.
- •4.3. Подготовка модели в виде пригодном к использованию функцией Minimize
- •4.4. Выполнение оптимизационных вычислений.
1. Постановка задачи
В курсовой работе необходимо:
разработать модель многоопорной колебательной системы (транспортного механизма);
на основе полученной модели произвести тестирование данного транспортного средства в зависимости от различных внутренних и внешних параметров, действующих на систему;
эргономически обоснованно реализовать выбор определенных параметров, влияющих на комфортабельность места водителя.
В качестве инструментариев к реализации поставленной задачи необходимо использовать следующие пакеты:
MathCAD;
MATLAB.
4
2. Вывод системы формул для расчёта оптимизационной модели автомобиля
2.1. Расчётная схема многоопорной машины с указанием варьируемых параметров
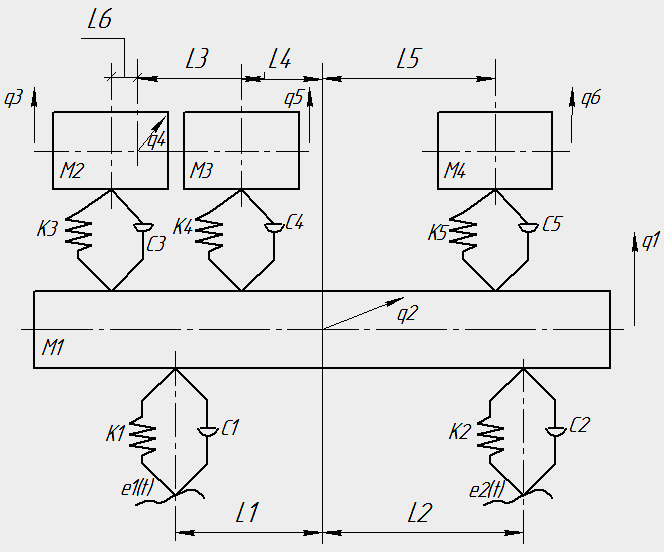
Кратко
охарактеризуем её. Машина представляет
собой корпус М1,
который получает кинематическое
воздействие от дороги
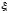 ,
,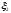 посредством двух опор. Эти опоры состоят
из параллельно соединённой пружины и
демпфера (
посредством двух опор. Эти опоры состоят
из параллельно соединённой пружины и
демпфера (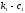 )
и (
)
и (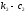 ).
Сверху на корпусе М1
расположены массы М2,
М3
и М4.
Эти массы соединяется с корпусом М1
при помощи трех опор: соединённых
параллельно пружины и демпфера (
).
Сверху на корпусе М1
расположены массы М2,
М3
и М4.
Эти массы соединяется с корпусом М1
при помощи трех опор: соединённых
параллельно пружины и демпфера (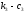 ),
(
),
(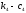 )
и (
)
и (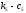 ).
Расстояниеoт
центра корпуса до опор (
).
Расстояниеoт
центра корпуса до опор ( )
и
(
)
и
(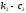 )
равны
l1
и
l2
соответственно. Расстояние от центра
корпуса до опор (
)
равны
l1
и
l2
соответственно. Расстояние от центра
корпуса до опор (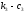 )
и
(
)
и
(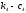 )
равноl6+l3+l4
и l4
соответственно.
Расстояние от центра корпуса до опор
(
)
равноl6+l3+l4
и l4
соответственно.
Расстояние от центра корпуса до опор
(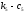 )
равноl5.
Запишем исходные данные модели:
)
равноl5.
Запишем исходные данные модели:
Параметры пружин, демпферов; длины, моменты инерции, функции дороги
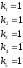
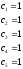
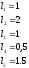
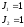
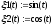
![]()
![]()
Для
оптимизации было выбрано линейное
ускорение массы М2
при варьировании параметров
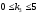 ,
,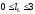 .
.
5
2.2. Выбор обобщенных перемещений.
Целесообразно
рассматривать относительные перемещения
 ,
,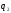 ,
,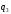 ,
,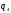 ,
,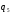 ,
,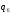 ,
которые отсчитываются относительно
земли:
,
которые отсчитываются относительно
земли:
q1 — вертикальное перемещение массы корпуса относительно грунта;
q2 — угол поворота корпуса относительно горизонта;
q3 — вертикальное перемещение массы М2 относительно грунта;
q4 — угол поворота массы М2 относительно горизонта;
q5 — вертикальное перемещение массы М3 относительно грунта;
q6 — вертикальное перемещение массы М4 относительно грунта;
В дальнейшем будем использовать в формулах для кинетической энергии относительные перемещение, а в формулах для удлинения пружин – обобщённые. Этот подход усложнит формулу кинетической энергии, однако упростит формулы для потенциальной энергии и диссипативной функции.
6
2.3. Составление выражений для удлинения и скорости удлинения упругих элементов
Перед началом записи выражений удлинения упругих элементов, определим следующие правило знаков: знак “-” будет браться, если упругий элемент сжимается, знак “+“ будет браться, если упругий элемент растягивается.
Запишем
значение удлинения для каждой из
присутствующих в многоопорном механизме
пружин:
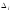
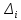 ,
гдеi
соответствует
номеру пружины:
,
гдеi
соответствует
номеру пружины:
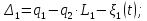
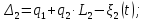

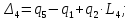
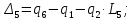
Таким образом, выражения для скоростей удлинения примут вид:
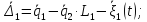
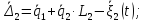
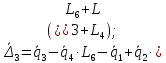
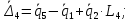
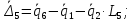
Записав абсолютные перемещения и выражения для удлинения упругих элементов, а также выражения для скоростей, имеем все данные для составления выражений кинетической, потенциальной энергий и диссипативной функции.
7
2.4. Полная кинетическая энергия системы.
Ее выражение и частные производные
Полная кинетическая энергия системы:
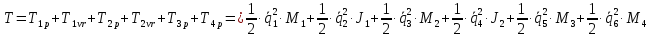
Вычислим частные производные вида:
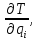
Они понадобятся нам для составления уравнения Лагранжа 2-го рода.
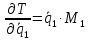
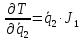
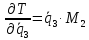
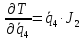
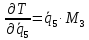
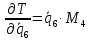
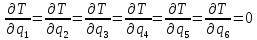
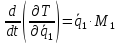
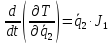
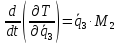
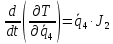
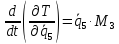
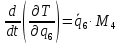
8
2.5. Полная потенциальная энергия системы.
Ее выражение и частные производные
Выражение для потенциальной энергии системы:
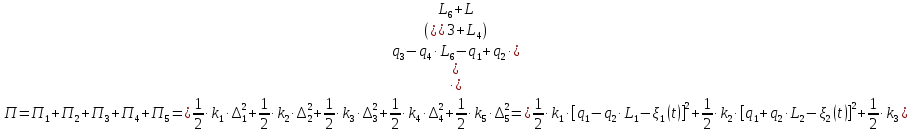
Определим частные производные вида:
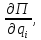
которые понадобятся при составлении уравнений Лагранжа 2-го рода.
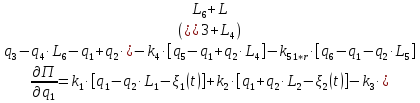
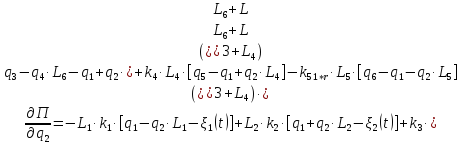
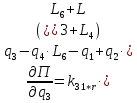
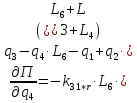
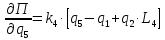
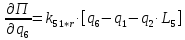
9
2.6. Диссипативная функция. Ее выражение и частные производные
Выражение для диссипативной функции:
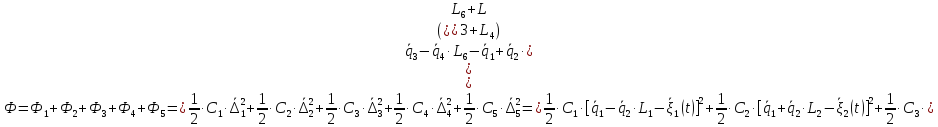
Найдем частные производные вида:
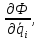
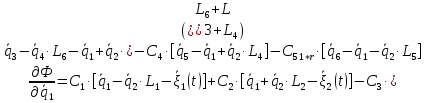
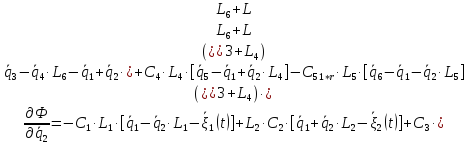
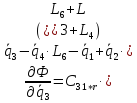
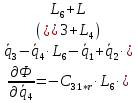
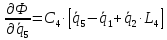
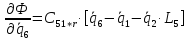
10
2.7. Составление системы уравнений Лагранжа 2-го рода
В систему уравнений Лагранжа второго рода (количество уравнений равно количеству неизвестных, т.е. количество уравнений равно шести) будут входить уравнения типа:
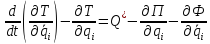
где
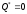 - вектор обобщённых внешних воздействий
(на модель оказывают воздействие только
функции дороги, поэтому этот вектор
равен нулю),
- вектор обобщённых внешних воздействий
(на модель оказывают воздействие только
функции дороги, поэтому этот вектор
равен нулю),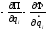 - найденные ранее частные производные
от потенциальной энергии и диссипативной
функции.
- найденные ранее частные производные
от потенциальной энергии и диссипативной
функции.
Система Лагранжа 2-го рода:
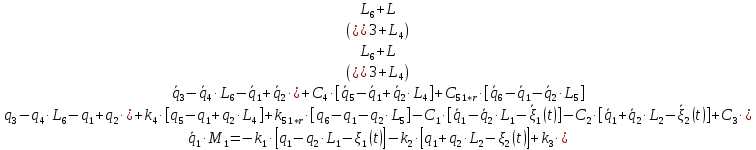
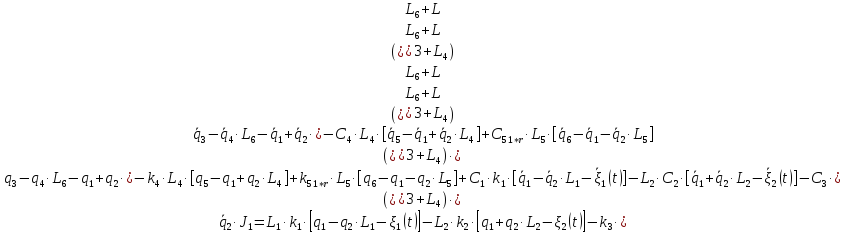
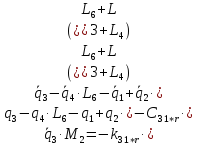
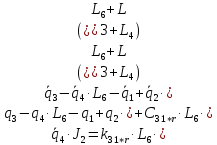

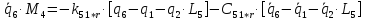
11
2.8. Сведение системы ОДУ 2-го порядка к системе ОДУ 1-го порядка в канонической форме Коши
Для того чтобы свести систему ОДУ Лагранжа 2-го рода к системе ОДУ 1-го рода в канонической форме Коши, введём следующие новые переменные.


Заменив, получим:
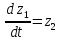
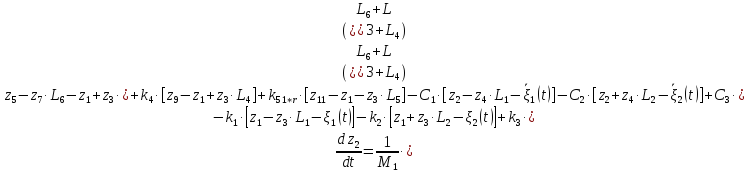
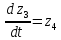
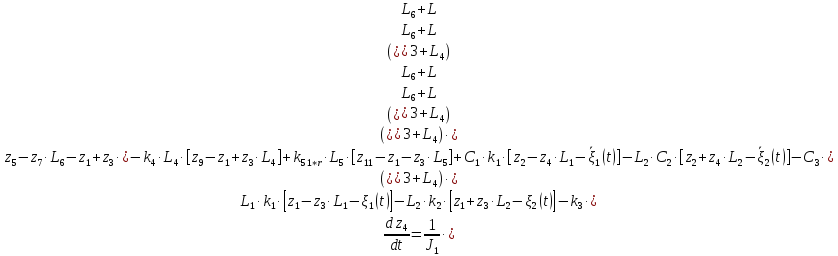
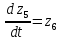
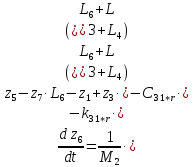
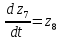
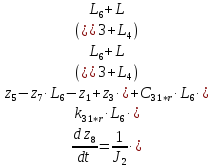
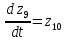
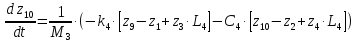
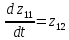
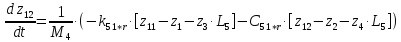
Система
значений вида
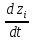 является системой, пригодной для решения
пакетамиMathCAD
и MATLAB.
является системой, пригодной для решения
пакетамиMathCAD
и MATLAB.
12
3. ТЕСТИРОВАНИЕ ПОЛУЧЕННЫХ УРАВНЕНИЙ
Для того, чтобы проверить правильность составленных уравнений, нужно воспроизвести такую ситуацию, в которой поведение системы можно предугадать. Тогда моделируя такую ситуацию, можно сравнить, совпадают ли наши предположения с полученными результатами, чем и определить правильность составления системы ОДУ.
Тест
№ 1:
принимаем функции дороги
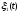 ,
,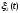 равными
нулю.
равными
нулю.
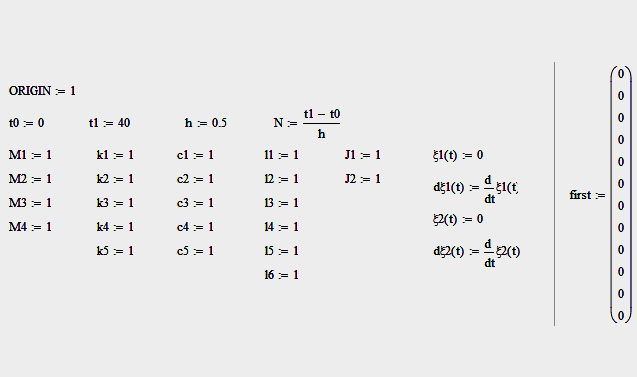
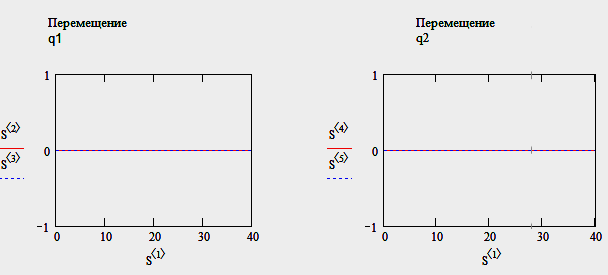
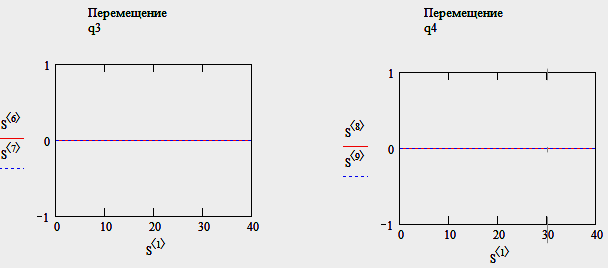
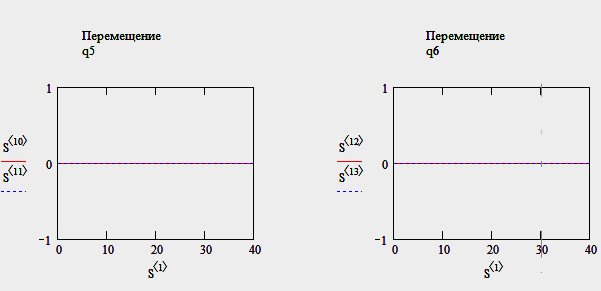
13
Результат – в отсутствии кинематического воздействия дороги система не колеблется, т.е. все перемещения (углы поворота) и скорость их изменения равны нулю.
Тест
№ 2:
задаем очень большую жесткость для
пружин, соединяющих массы М1 с М2 и М1 с
М3
 )
и задаем линейное перемещение массы М1q1=2.
)
и задаем линейное перемещение массы М1q1=2.

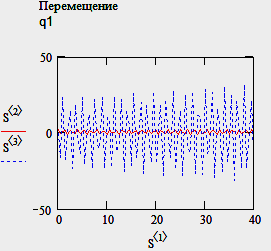
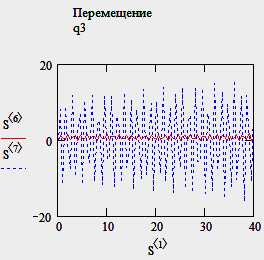
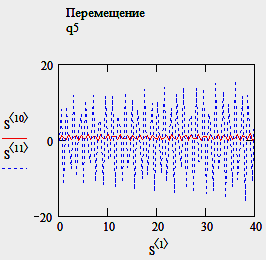
Результат: массы оказались «связанными», их колебания почти идентичны.
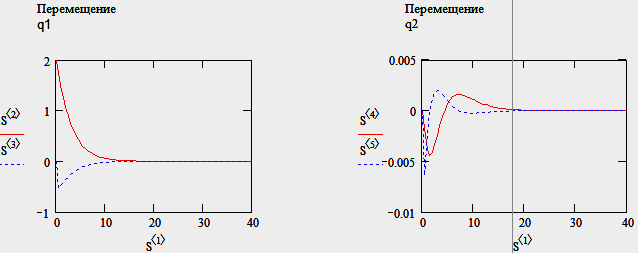
Тест № 3: разрываем связь между корпусом и массой М2 (k3=c3=0).


14
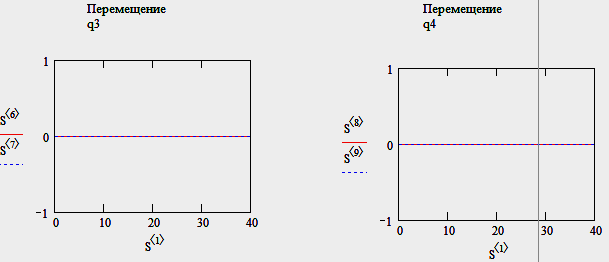
Результат – т.к. масса М2 получает кинематическое воздействие дороги через корпус, то разорвав связь между корпусом и массой М2, мы получаем отсутствие колебаний (поворотов) массы М2.
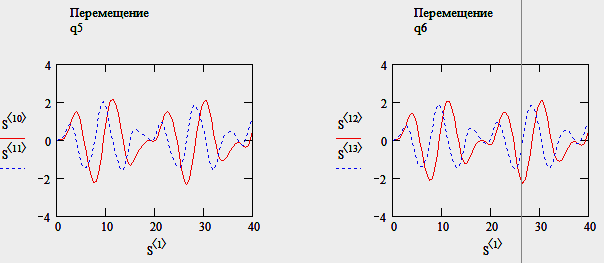
Тест № 4: добавляем демпферы.

15
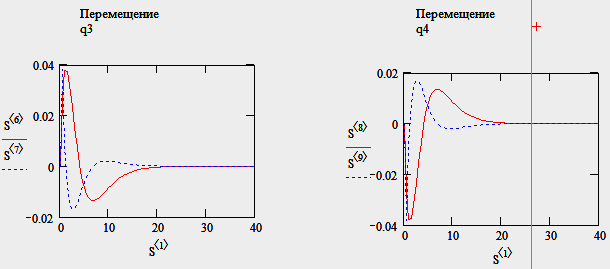
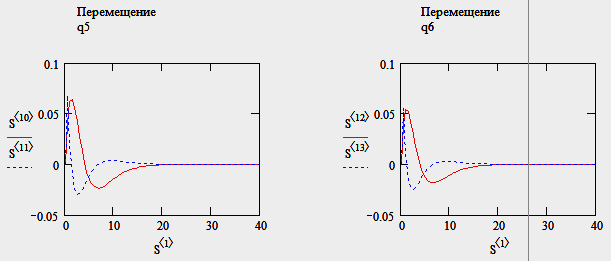
Результат – наблюдаем угасание колебаний.
Тест
№ 5:
разрываем связь между корпусом и массой
М2 и М4 (k3=c3=k5=c5=0),
принимаем функции дороги
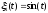 ,
,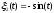 .
.

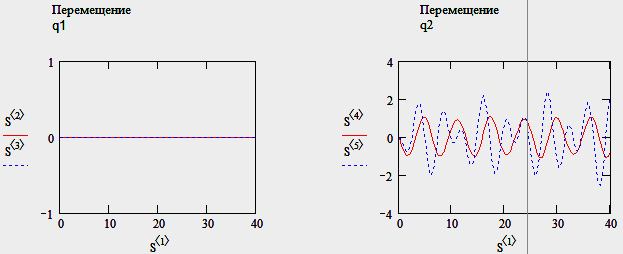
16
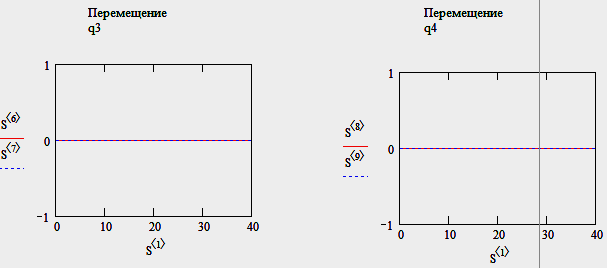
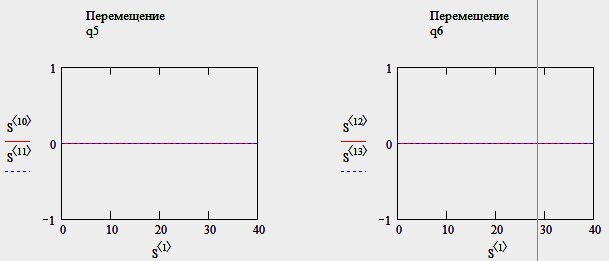
Результат – т.к. масса М3 находится посередине рамы и получает кинематическое воздействие дороги через корпус, то образовав связь между корпусом и массой М3, мы получаем только наличие поворотов рамы.
17
4. ОПТИМИЗАЦИЯ НА ОСНОВЕ ПАРАМЕТРОВ K3, L6
4.1. Разработка программы для решения системы ОДУ в канонической форме Коши средствами MathCAD, на основе предложенного алгоритма
Для решения системы ОДУ в каноническом виде Коши используем метод Рунге-Кутта 4-го порядка. Приращение переменной можно выразить по следующей формуле:
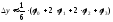 ,
,
где:
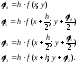
Тогда программная реализация данного метода будет иметь вид:

В результате вычислений и всех тестов, получается полное совпадение результатов с результатами, полученными при помощи встроенной функции Rkadapt (Приложение 1).
18
4.2.Изучение встроенной процедуры оптимизации в MathCAD
Рассмотрим встроенную в MathCAD функцию Minimize.
Данная функция предназначена для поиска такого значения независимой перемененной, при котором значение функции будет минимально. Опишем синтаксис данной функции.
Перед
началом блока оптимизации пишется
ключевое слово Given,
которое позволяет определить пакету
MathCAD,
где начинается блок минимизации. После
ключевого слова Given
перечисляются переменные с указанием
граничных условий. По этим переменным
MathCAD
и будет искать минимальное значение
функции. Исходя из моего примера,
следующая запись (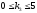 и
и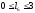 )
означает, чтоMathCAD
будет искать минимальное значение
функции, изменяя 2 параметра -
)
означает, чтоMathCAD
будет искать минимальное значение
функции, изменяя 2 параметра -
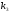 и
и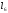 .
После перечисления переменных следует
вызов функцииMinimize.
Синтаксис у функции следующий:
.
После перечисления переменных следует
вызов функцииMinimize.
Синтаксис у функции следующий:
Minimize(<имя_функции>,<параметр1>,<…>,<параметрn>),
где - <имя_функции> - имя той функции, минимальное значение которой необходимо найти, <параметр1>…<параметрn> - список параметров, по которым функция Minimize будет искать минимум.
Необходимо заметить, что количество параметров и их порядок следования должен быть таким же, как и в функции, минимальное значение которой мы ищем.
Так же необходимо отметить, что чем больше входных параметров у функции Minimize, тем большее количество времени занимает поиск минимального значения. Отсюда следует вывод – количество входных параметров у функции Minimize (как было замечено выше, и у минимизированной функции тоже) должно быть минимально.
Функция Minimize возвращает матрицу-столбец с перечислением оптимальных параметров.
19
