
86-2008(методичка-математика)
.pdf
Тогда |
|
|
t 3, |
3 |
|
|
|
|
|
t 2 , |
dx 3t 5dt . |
|
||||
2x 1 |
2x 1 |
|
||||||||||||||
|
|
|
3t 5dt |
|
|
|
|
|
|
|
t 2 |
|
(t 2 1) 1 |
|
||
|
I |
|
|
3 |
|
|
dt 3 |
|
|
dt |
||||||
|
t 3(1 t 2 ) |
1 t 2 |
1 t 2 |
|||||||||||||
|
3 dt 3 |
1 |
|
|
dt 3t 3arctg t C |
|
||||||||||
|
|
|
|
|||||||||||||
|
1 t 2 |
|
||||||||||||||
3 6 2x 1 3 arctg 6 2x 1 C .
г) Интегрирование тригонометрических выражений.
При вычислении интегралов sin n x cosm x dx , где n, m –
целые числа рекомендуется использовать следующие приемы: I. Если оба показателя n и m - неотрицательные четные
числа, то применяют формулы понижения степени:
|
|
2sin 2 x 1 cos 2x, |
|
2 cos 2 x 1 cos 2x . |
|
|
||||||||||||||||||||||||||||
|
4 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
2 |
|
|||||||
cos |
|
x dx |
|
|
|
1 cos 2x |
dx |
|
|
|
|
1 2 cos 2x cos |
|
2x dx |
||||||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 2 cos 2x |
|
|
(1 cos 4x) dx |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 cos 2x |
|
|
|
cos 4x dx |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
3 |
dx |
1 |
cos 2x dx |
|
1 |
cos 4x dx |
|
|
||||||||||||||||||||||
|
|
|
8 |
|
2 |
|
8 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
x |
sin 2x |
|
|
sin 4x |
C . |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
32 |
|
|
|
|
||||||||
II. Если n и m - натуральные числа такие, что хотя бы одно из них нечетное, то в случае нечетного m полагают
41
sin x t , а в случае нечетного n полагают |
cos x t и |
применяют формулу |
|
sin 2 x cos 2 x 1. |
|
sin5 x cos4 x dx sin 4 x cos4 x sin x dx
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
sin 4 x cos 4 x d cos x (1 cos 2 x) |
|
cos 4 x d cos x |
||||||||||||||||||||
|
|
|
(1 t 2 )2 t 4 dt (t 4 2t 6 t8 ) dt |
|
|
|
||||||||||||||||
|
|
5 |
|
t |
7 |
|
t |
9 |
|
|
cos |
5 |
x |
|
2 cos |
7 |
x |
|
cos |
9 |
x |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
2 |
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
5 |
|
7 |
|
9 |
|
5 |
|
|
7 |
|
|
|
9 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача №8
Вычислить несобственный интеграл или показать, что он расходится.
Решение. Напомним определение несобственного интеграла. Если существует конечный предел
b
lim f (x) dx , b a
то этот предел называют несобственным интегралом от функции f(x) на промежутке [a, +∞) и обозначают
f ( x ) dx .
a
Следовательно, по определению
|
|
b |
f (x) dx |
lim |
f (x) dx . |
a |
b a |
|
42
В этом случае говорят, что несобственный интеграл сходится, в противном случае – расходится.
|
1 |
|
|
b |
|
|
1 |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|||||
1) |
|
|
|
|
dx |
lim |
|
|
|
|
dx |
lim |
(arctg x) |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1 x2 |
|
|
x2 |
|
1 |
|
|
||||||||||||||||||
|
1 |
|
b |
1 |
1 |
|
b |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
lim |
(arctg b arctg 1) |
|
lim (arctg b |
) |
|
|
|
|
|
. |
|||||||||||||
|
b |
|
|
|
|
|
|
b |
|
|
|
|
4 |
2 |
|
|
4 |
|
4 |
||||||
|
|
|
b |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
b |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
cos |
|
|
lim cos 2x dx |
|
|
|
|
|
|
|||||||||||||||
2) |
2x dx |
lim |
|
sin 2x |
|
|
|
|
|
||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
b |
|
|
|
|
|
|
b |
|
|
|
|
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
lim |
sin 2b sin 0 |
1 |
|
lim |
sin 2b. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
2 b |
|
|
|
|
|
2 b |
|
|
|
|
|
|
|
|
|
|
|||||||
Так как полученный предел не существует, то интеграл расходится.
dx |
|
b dx |
|
|
b |
|
|||
|
|
|
|
||||||
3) |
|
lim |
|
|
|
lim (ln x) |
1 |
|
|
x |
x |
||||||||
b |
|
b |
|
||||||
1 |
1 |
|
|
|
|||||
lim (ln b ln1) b
lim |
ln b . |
|
|
||
b |
|
|
|
|
|
В данном случае интеграл расходится. |
|||||
|
|
|
Задача №9 |
|
|
Вычислить |
площадь |
фигуры, |
ограниченной линиями |
||
y x 3 и |
y 6x x2 7 . Сделать чертеж. |
||||
Решение. |
Если фигура ограничена графиками функций |
||||
y1(x) и |
y2(x) |
y1(x) y2 (x) |
и соответствующими |
||
отрезками прямых |
x a и |
x b , то ее площадь вычисляется |
|||
по формуле
43

b
S( y2 (x) y1(x))dx . a
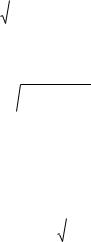
В нашем случае y1(x) x 3 и y2 (x) 6x x2 7 , a и b
– абсциссы точек пересечения указанных прямых (рис. 3). y
2
0 |
1 |
3 |
4 |
-2
|
|
|
|
|
|
|
|
Рис. 3 |
|
|
|
|
|
|
|
||||
Найдем эти значения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
6x x2 7 x 3, |
|
|
||||||||||||
|
|
|
|
|
|
|
x2 5x 4 0 , |
|
|
|
|||||||||
|
|
|
|
|
|
|
x1 1, |
x2 4 . |
|
|
|
||||||||
Найдем площадь фигуры: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4 |
|
(6x x |
2 |
7) (x |
|
|
|
4 |
|
|
|
||||||||
S |
|
|
3) dx |
5x |
|||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
5 |
|
2 |
|
1 |
|
|
3 |
|
|
|
4 |
|
9 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
x |
|
|
|
|
x |
|
|
4x |
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
1 |
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x
x |
2 |
|
|
4 dx |
|
|
|
|
44
|
|
|
|
|
Задача №10 |
|
|
|
Вычислить |
длину |
дуги |
кривой, |
заданной |
уравнением |
|||
|
|
|
|
|
|
|
|
|
y 9 x2 ; |
0 x 3. |
|
|
|
|
|||
Решение. |
|
Длина |
дуги |
кривой, |
заданной |
уравнением |
||
y f (x) при |
a x b , |
вычисляется по |
формуле |
|||||
b
L 1 y 2 (x) dx . a
1 y 2 (x) dx . a
В рассматриваемом случае 1 y |
2 |
(x) |
9 |
. Поэтому |
|||||||||||||
|
|||||||||||||||||
9 x2 |
|||||||||||||||||
|
|||||||||||||||||
3 |
|
dx |
|
|
x |
|
|
3 |
|
|
|
|
|
3 |
|
||
|
|
|
|
|
|
|
|
|
|
||||||||
L 3 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
3arcsin |
|
|
|
|
3(arcsin 1 arcsin 0) |
|
. |
||||||
|
|
|
|
|
|
|
|
||||||||||
0 |
|
9 x |
2 |
|
3 |
|
|
0 |
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Задача №11
Вычислить объем тела, полученного при вращении
вокруг |
оси |
Ox |
фигуры, |
ограниченной |
линиями |
||
y 1 |
1 |
, |
y 0, |
x 1, |
x 3 . Сделать чертеж. |
|
|
|
|
||||||
|
x |
|
|
|
|
|
|
Решение. Объем V тела, образованного вращением вокруг |
|||||||
оси Ox фигуры, |
ограниченной графиком функции |
y y(x) , |
|||||
отрезками прямых x a и x b и отрезком оси Ox , равен
b
V y 2 (x) dx .
a
Изобразим указанную в условии задачи фигуру (рис.4). По формуле находим:
45

3 |
|
1 2 |
|
|
|
|
3 |
|
2 |
|
|
|
1 |
|
||||
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
dx 1 |
|
x |
|
|
2 |
dx |
|||||||||
1 |
|
|
x |
|
|
|
|
1 |
|
|
x |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
|
3 |
8 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||||
x |
|
2 ln x |
|
|
|
|
|
|
|
|
2 ln 3 . |
|||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
x |
|
|
1 |
3 |
|
|
|
|
|||||
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
3 |
x |
|
|
|
Рис. 4
46

Приложение 1
Таблица производных простейших элементарных функций.
I.(С) = 0.
II. (x ) x 1, в частности |
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|
, ( x ) |
|
|
|||||||||
|
|
|
|
|
|
|
. |
|||||
|
x2 |
|
|
|
||||||||
|
|
х |
|
|
|
|
2 x |
|
|
|||
III. |
(logа х) = |
1 |
|
logа е, в частности (ln х) = |
1 |
. |
||||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|||
IV. |
|
(a x ) a x ln a, в частности, |
(e x ) e x . |
|
|
|||||||||||||||
V. (sin х) = cos х. |
|
|
|
|
|
|
|
|
|
|||||||||||
VI. |
|
(cos х) = sin х. |
|
|
|
|
|
|
|
|
|
|||||||||
VII. |
|
( tg x ) = |
1 |
|
. |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
cos |
2 x |
|
|
|
|
|
|
|
|
|
|||||||
VIII. (ctg x) = |
|
|
|
1 |
|
|
|
. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
sin 2 x |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
IX. |
|
(arcsin х) = |
|
1 |
|
|
|
. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1 x2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
X. |
(arccos x) = |
|
1 |
|
|
|
|
. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 x2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
XI. (arctg x) = |
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 x2 |
|
|
|
|
|
|
|
|
|
|||||||||||
XII. (arcctg x) = |
|
1 |
|
. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||
1 x2 |
|
|
|
|
|
|
|
|||||||||||||
XIII. |
(sh х) = ch х. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
XIV. |
(ch х) = sh х. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
47

XV. (th x) = |
|
|
1 |
|
. |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
ch 2 x |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
XVI. |
(cth x) = |
|
|
1 |
|
. |
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sh2 x |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 2 |
|
|
Таблица интегралов простейших элементарных функций |
|||||||||||||||||||||||||
I. |
x dx |
x 1 |
C |
|
1 . |
|||||||||||||||||||||
|
1 |
|
||||||||||||||||||||||||
II. |
|
dx |
|
ln |
|
x |
|
C. |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
III. |
|
|
|
|
dx |
arctg x C. |
|
|
||||||||||||||||||
1 |
x2 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
IV. |
|
|
|
|
dx |
|
|
|
|
|
arcsin x |
C. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1 |
x2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
V. a xdx |
|
|
a x |
|
|
|
0 a 1 . |
|||||||||||||||||||
|
C |
|
||||||||||||||||||||||||
ln a |
|
|||||||||||||||||||||||||
VI. |
e x dx e x C. |
|
|
|
|
|||||||||||||||||||||
VII. sin x dx cos x C.
VIII. cos x dx sin x C.
IX . dx tg x C . cos 2 x
48

X. |
|
|
|
dx |
ctg x C. |
|
|
|
||||||||||||||||||
sin 2 x |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
XI. |
|
|
|
|
|
dx |
|
|
|
|
1 |
|
ln |
x a |
C |
(a 0) . |
||||||||||
|
x2 a2 |
2a |
x a |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
XII. |
|
|
|
|
|
dx |
|
|
|
ln |
x |
|
x2 k |
C. |
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
x2 k |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
XIII. |
|
|
|
dx |
|
|
|
|
|
1 |
arctg |
x |
C. |
|
||||||||||||
|
x2 a2 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
a |
|
|
|
||||||||||||
XIV. |
|
|
|
dx |
|
|
|
|
arcsin |
|
x |
|
C. |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
||||||||||||||
|
|
|
a2 x2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1.Пискунов Н. С. Дифференциальное и интегральное исчисления / Н.С. Пискунов.- М.: Наука, 1985. Т.1.
2.Данко П.Е. Высшая математика в упражнениях и
задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - М.: Высш. шк., 1986. Ч. 1.
3.Рябушко А.П. и др. Сборник индивидуальных заданий по высшей математике / А.П. Рябушко. - Минск: Высш. шк.,
1990. Ч.1.
4.Каплан И.А. Практические занятия по высшей математике / И.А. Каплан. – Харьков: ХГУ, 1973. Ч. 1, 2.
5.Кузнецов Л.А. Сборник заданий по высшей математике
/Л.А. Кузнецов - М.: Высш. шк., 1994. 172 с.
49
|
СОДЕРЖАНИЕ |
|
|
1. |
Общие рекомендации студенту-заочнику к изучению |
|
|
|
курса высшей математики . . . . . . . . . . |
. . . . . . . . . . . . . . . |
1 |
2. |
Правила выполнения и оформления контрольных работ |
3 |
|
3. |
Программа курса “Высшая математика” для студентов- |
|
|
|
заочников инженерно-технических специальностей. . . . |
3 |
|
4. |
Вопросы для самопроверки к контрольной работе №2. . |
5 |
|
5. |
Контрольная работа №2. . . . . . . . . . . |
. . . . . . . . . . . . . . . |
6 |
6. |
Примеры решения задач к контрольной работе №2 . . . . |
23 |
|
|
Приложение 1 . . . . . . . . . . . . . . . . . . . . |
. . . . . . . . . . . . . . . |
45 |
|
Приложение 2 . . . . . . . . . . . . . . . . . . . . |
. . . . . . . . . . . . . . . |
46 |
|
Библиографический список . . . . . . . |
. . . . . . . . . . . . . . . |
47 |
50
