
Теория графов
.pdfВ частности, в полном графе Кn |
любые две различные |
вершины связаны ребром, следовательно |
(Kn ) n . |
Многие практические задачи сводятся к построению |
|
раскрасок графа.
Пример 1: Требуется прочитать несколько лекций за кротчайшее время. Пусть при этом чтение одной лекции занимает 1 час. Некоторые лекции не могут читаться одновременно из-за того, например, что их читает один и тот же лектор. В графе G вершинам соответствуют лекции и две вершины в нем смежны тогда и только тогда, когда соответствующие им лекции нельзя читать одновременно. Следовательно, любая раскраска графа определяет допустимое расписание. В результате любое допустимое расписание определяет раскраску графа. При чём оптимальное расписание соответствует раскраске с минимальным числом цветов и, следовательно, оно определяет минимальное число часов, необходимых для прочтения всех лекций. Оно равно (G) .
Пример 2: Рассмотрим граф, вершины которого страны,
а рёбра – границы стран. Числу |
(G) |
соответствует наимень- |
шее число красок, необходимых для раскрашивания карты так, чтобы никакие две соседние страны небыли окрашены в один цвет.
Существуют также задачи связанные с раскраской ребер мультиграфа. Раскраска ребер в мультиграфе G может быть определена с помощью раскраски вершин реберного мультиграфа L(G). Для произвольного неориентированного мультиграфа G=(V,E,P) реберным мультиграфом L(G) называется
тройка (E, V, P`) , |
где P` является подмножеством прямого |
||||
произведения |
|
E V E , |
и |
выполняется |
усло- |
P |
|||||
|
тогда и только тогда, когда в мультиграфе G |
||||
вие (u, a,v) P |
|||||
вершина а является концом ребер u и v. Раскраской ребер мультиграфа G называется раскраска вершин мультиграфа
L(G).
Практическое приложение. Проводится монтаж радиоаппаратуры. Чтобы не перепутать проводники необходимо их
50
раскрасить так, чтобы два проводника, идущие к одной плате, имели разные цвета, В этом примере вершинам мультиграфа соответствуют платы, а ребрам - проводники. Определение минимального набора цветов в проводниках соответствует решению задачи о раскраске рёбер соответствующего мультиграфа.
Неорграф называется бихроматическим, если
(G)
2
.
Теорема. Пусть G – неорграф без петель, имеющий хотя бы одно ребро. Тогда следующие утверждения эквивалентны:
1)G – бихроматический граф.
2)G – двудольный граф.
3)G –не содержит циклов нечетной степени.
Следствие. Если G – лес, то (G) 2 .
Для любого неорграфа G без петель справедливо неравенство (G) deg(G) 1, где deg(G) – максимальная степень вершин графа G.
8.3.Алгоритм последовательной раскраски.
1.Произвольная вершина графа принимает цвет 1.
2.Если вершины a1, …, ai раскрашены цветом 1,2, …,l (l i), то новой произвольно взятой вершине ai+1 приписывается минимальный цвет, неиспользованный при раскраске вершин, смежных с ai+1.
Для некоторых классов графов последовательная раскраска является минимальной, однако, в общем случае, это не всегда так.
Раскраска планарного графа. Теорема (Горбатов). Хроматическое число планарного графа не превышает четырех. (Горбатов «Фундаментальные основы дискретной математи-
ки», с. 244)
51

9.ПОКРЫТИЯ И НЕЗАВИСИМОСТЬ.
9.1.Покрывающие множества вершин и ребер.
Говорят, что вершина покрывает инцидентные ей ребра, а ребро покрывает инцидентные ему вершины.
Множество вершин, которое покрывает все ребра графа, называется вершинным покрытием. Наименьшее число вершин во всех вершинных покрытиях называется числом вершинного покрытия и обозначается 0.
Например:
1.Для полного графа 0(Kn)=n-1.
2.Для полного двудольного графа 0(Km,n)=min(m,n).
3. Для графа с изолированными вершинами 0(
K |
n |
|
)=0.
4.Для несвязного графа 0(G1 G2)= 0(G1)+0(G2), где G1 и G2 – компоненты связности.
Множество ребер, которые покрывают все вершины называется реберным покрытием. Наименьшее число ребер во всех реберных покрытиях называется числом реберного покрытия и обозначается 1. Заметим, что 1 не определено для графа с изолированными вершинами.
Например:
1.Для четного цикла 1(K2n)=n, для нечетного цикла
1(K2n+1)=n+1.
2.Для полного графа с четным числом вершин
1(K2n)=n, для полного графа с нечетным числом вершин 1(K2n+1)=n+1.
3.Для полного двудольного графа 1(Km,n)=max(m,n).
9.2.Независимые множества вершин и ребер.
Множества вершин называются независимыми, если никакие две из них не смежны. Наибольшее число вершин в независимом множестве вершин называется вершинным числом независимости и обозначается 0.
52

Например:
1.Для полного графа 0(Kp)=1.
2.Для полного двудольного графа 0(Km,n)=max(m,n)
3. Для графа с изолированными вершинами 0(
K |
p |
|
)=p.
4. Для несвязного графа 0(G1 G2)= 0(G1)+ 0(G2) Множества ребер называются независимыми, если ни-
какие два из них не смежны. Наибольшее число ребер в независимом множестве ребер называется реберным числом независимости и обозначается 1. Независимое множество ребер называется также паросочетанием.
Например:
1.Для четного цикла 1(K2n)=n, для нечетного цикла
1(K2n+1)=n-1.
2.Для полного графа с четным числом вершин
1(K2n)=1, для полного графа с нечетным числом вершин 1(K2n+1)=n-1.
3.Для полного двудольного графа 1(Km,n)=min(m,n).
Для любого нетривиального графа числа независимости и покрытия связаны следующим соотношением 0+ 0 = 1+ 1
= p.
Замечание. Условия связности и нетривиальности гарантируют, что все четыре инварианта определены. Однако это условие является достаточным, но не является необходимым. Например, для графа Kn Kn заключения теоремы остаются справедливыми, хотя условие не выполнено.
Задача отыскания наибольшего независимого множества вершин (т.е. определение вершинного числа независимости 0) принадлежит к числу трудоемких.
В данном случае имеется возможность найти решение данной задачи «полным перебором» всех возможных вариантов в силу конечности их числа. Для выполнения данного алгоритма потребуется О(2Р) шагов.
При решении переборных задач большое значение имеет способ организации перебора. В данном случае это последовательность перечисления множеств. Наиболее известным спо-
53
собом организации перебора является поиск с возвратом. Иногда употребляется термин бектрекинг.
Идея поиска с возвратом состоит в следующем. Находясь в некоторой ситуации, изменяют её для того, чтобы найти решение. Если изменение не дало желаемого результата, то возвращаются в исходную позицию. Затем делается изменение другим образом и т.д. до тех пор пока не будут исчерпаны все возможности.
Применение метода поиска с возвратом не гарантирует эффективности. В худшем случае поиска с возвратом имеет тот же порядок, что и другие способы перебора.
Используя конкретную информацию о задаче, в некоторых случаях можно существенно сократить трудоемкость выполнения каждого шага перебора или уменьшить количество перебираемых вариантов. Такие методы называются методами улучшения перебора. Например, может оказаться, что некоторые варианты заведомо не могут привести к решению, а потому их можно не рассматривать.
9.3. Доминирующие множества.
Задача о наименьшем покрытии (ЗНП) является примером общей экстремальной задачи, к которой прямо или косвенно сводятся практические задачи. Эта задача может быть сформулирована в терминах доминирующего множества.
Определение. Для графа G(V,E) множество вершин S V называется доминирующим множеством, если для любой вершины v V выполняются условия: 1) либо v S, 2) либо существуют вершина s S и ребро (s,v).
Доминирующее множество называется минимальным, если его подмножество не является доминирующим. Доминирующее множество называется наименьшим, если число элементов в нем минимально.
Пример: Задача о пяти ферзях. Расставить их на шахматной доске так, чтобы они били всю доску. Это задача об отыскании наименьших доминирующих множеств.
54
Доминирование тесно связано с вершинной независимостью.
Теорема. Независимое множество вершин является максимальным тогда и только тогда, когда оно является доминирующим.
Независимое доминирующее множество вершин называется ядром графа.
Рассмотрим задачу. Пусть каждый вершине сопоставлена некоторая цепь. Требуется выбрать доминирующее множество с наименьшей суммарной ценой. Эта задача называется задачей о наименьшем покрытии (ЗНП). К этой задаче сводятся, например:
1)Задача о выборе переводчиков. Организации нужно нанять переводчиков с определенного множества языков. Каждый из имеющихся переводчиков владеет некоторыми иностранными языками и требует определенную зарплату. Требуется определить, каких переводчиков следует нанять, чтобы сумма расходов на зарплату была минимальной.
2)Задача о перевозке. Поставщику необходимо доставить товары своим потребителям. Имеется множество различных маршрутов, каждый их которых позволяет обслуживать определенное подмножество потребителей и требует определенных расходов. Требуется определить, какие маршруты следует использовать, чтобы все потребители были обслужены, а сумма транспортных расходов была наименьшей.
ЗНП могут быть сформулированы различными способами.
1) Пусть имеется конечное множество {V1,…, Vp} и семейство подмножеств этого множества {E1,…, Ep}. Каждому подмножеству Ei приписать вес. Найти покрытие E` (E` E) наименьшего веса. Из этой формулировки происходит название «задача о наименьшем покрытии».
2)ЗНП можно сформулировать как задачу линейного
p |
p |
|
программирования min ci xi при ограничениях |
tij x j |
1 |
i 1 |
j 1 |
|
55
(i=1,…,p), где ci0 xi=
1,если E E |
||
|
i |
|
противном |
||
0, в |
||
|
|
|
случае
tij=
1, если |
V E |
|||
|
|
i |
i |
|
противном случае |
||||
0, в |
||||
|
|
|
|
|
3) Дана булева матрица Т размера р на р. Каждому столбцу приписан вес cj. Найти такое множество столбцов минимальной стоимости, чтобы любая строка содержала единицу хотя бы в одном из выбранных столбцов.
ЗНП относиться к числу трудоемких задач, и для ее решения применяются переборные алгоритмы с теми или иными улучшениями. Связь ЗНП с другими задачами можно представить в следующем виде.
ЗНП
Наименьшее |
|
доминирующее |
ЗНП с единичными весами |
множество вершин |
|
|
Наибольшее независимое |
|
множество вершин |
Наименьшее |
|
доминирующее |
Наибольшее независимое |
множество ребер |
множество ребер |
На этой схеме стрелки от задачи А к задаче В означает, что решение задачи А влечет за собой решение задачи В.
56

10. КРАТЧАЙШИЕ МАРШРУТЫ В ГРАФАХ.
10.1. Расстояния в графах.
Пусть G(V, E) – связный неориентированный граф, a,b – две несовпадающие вершины. Длина кратчайшего (a, b) – маршрута называется расстоянием между вершинами a и b и обозначается (a, b).
Полагается, что (a, b)=0. Расстояние удовлетворяет аксиомам метрики:
1)(a, b)0
2)(a, b)=0 тогда и только тогда, когда a=b
3)(a, b)= (b, a) (свойство симметричности)
4)(a, b) (a, c)+ (c, b) (неравенство тре-
угольника)
Матрица P=pi,j , где pi,j = (ai, aj), называется матрицей расстояний. Заметим, что матрица расстояний симметрична
(PT=P).
E(a)=max{ (a,b)|b V} – эксцентриситет вершины a. Эксцентриситет вершины равен расстоянию от данной точки до наиболее удаленной от нее.
Эксцентриситет e(a1) равен наибольшему из чисел стоящему в i-ой строке матрицы расстояний.
Максимальный среди всех эксцентриситетов вершин называется диаметром графа G и обозначается d(G). d(G)=max
e(ai)
Вершина a называется периферийной, если ее эксцен-
триситет e(a)=d(G).
Минимальный из эксцентриситетов графа G называется его радиусом и обозначается r(G). r(G)=min{e(a)|a V}
Вершина a графа G называется центральной, если e(a)=r(G).
Множество всех центральных вершин графа называются его центром.
57
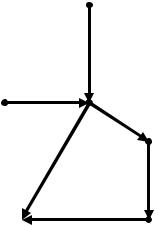
Пример: Рассмотрим граф
|
0 |
||
|
|
1 |
|
|
|
||
Матрица расстояний: P= |
|
2 |
|
|
|||
|
|
||
|
1 |
||
|
|
2 |
|
|
|
||
4  5
5
|
|
|
|
2 |
|
|
|
1 |
|
3 |
|
1 |
2 |
1 |
2 |
||
0 |
1 |
1 |
1 |
|
|
|
|||||
1 |
0 |
2 |
1 |
|
|
|
|||||
|
|
|
|
||
1 |
2 |
0 |
1 |
||
1 |
1 |
1 |
0 |
|
|
|
|||||
Отсюда e(1)=2; e(2)=1; e(3)=2 e(4)=2; e(5)=2, следова-
тельно, периферийными вершинами будут являться (1, 3, 4, 5). R(G)=1 Центром графа {2}. В полном графе d(Kn)=r(Kn)=1
Задача нахождения центральных вершин возникает в практической деятельности людей. Например, пусть в графе вершины соответствуют населенным пунктам, а ребра - дорогам между ними. Требуется оптимальным образом разместить больницы, пункты обслуживания и т.п. Местами размещения таких объектов должны быть центральные вершины графа. Реальные задачи отличаются от идеальных тем, что приходится учитывать расстояния между населенными пунктами, время проезда, стоимость и т.д. Для учетов этих параметров используются взвешенные графы.
Пусть G(V, E) – взвешенный граф, в котором вес каждой дуги (a,b) есть некоторое вещественное число (a,b).
Весом маршрута a1, a2, …, an, an+1 называется число
n |
|
= |
(ai , ai 1 ) . |
i 1 |
|
58
Взвешенным расстоянием ( расстояние) (a,b) между вершинами a и b называется минимальный из весов (a,b) – маршрутов.
(a,b) – маршрут, вес которого равен (a,b) называется кратчайшим (a,b) маршрутом графа G.
Взвешенным эксцентриситетом e (a) вершины a назы-
ваются числа max{ (a,b)|b V}.
Взвешенной центральной вершиной графа G называется вершина a, для которой e (a)=min{ e (b)|b V}.
Взвешенный эксцентриситет центральной вершины называется взвешенным радиусом графа G, и обозначается как r (G).
10.2. Алгоритм Форда-Беллмана.
Пусть G(V, E) – взвешенный граф, имеющий n вершин и матрицу весов W=( ij). Требуется найти взвешенное расстояние от фиксированной вершины ai V называемой источником, до всех вершин графа G.
Предполагается, что в G отсутствуют контуры с отрицательным весом т.к. двигаясь по такому контуру достаточное количество раз можно получить маршрут меньший любого, наперед заданного, числа. Т.о. в этом случае задача нахождения расстояния становиться бессмысленной.
Алгоритм Форда-Беллмана заключается в том, что зада-
ется строка Д(1)=(d(1)1, d(1)2, d(1)3, …, d(1)n), в которой d(1)i=0, d(1)j= ij, если i j.
Предполагается, что все дуги ij= , если (ai, aj) E Далее определяется строка Д(2)=(d(2)1, d(2)2, d(2)3, …, d(2)n),
где d(2)j=min{d(1)j, d(1)k+ kj}
Заметим, что d(2)j – минимальный из весов (ai, aj) маршрутов состоящих не более чем из двух дуг.
59
