
Теория графов
.pdf
2. ПРЕДСТАВЛЕНИЯ ГРАФОВ В ЭВМ И ОПЕРАЦИИ НАД НИМИ.
2.1. Матричные способы задания графов.
Матрицей смежности графа G=(V,E) с n вершинами называется квадратная матрица А порядка n, элементы которой определяются следующим образом:
а) в случае неориентированного графа
|
|
|
a |
|
1, если вершины v и |
v |
|
смежны, |
|
|
|
|
|
|
|
i |
|
j |
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
i, j |
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
в противном случае; |
|
|
|||
|
|
б) для ориентированного графа |
|
|
|
|
|
||||
a |
|
1, если существуетдуга из вершины v в вершину v |
, |
||||||||
|
|
|
|
|
|
|
i |
j |
|
||
|
|
|
|
|
|
|
|
|
|||
i, j |
|
0 |
|
- |
|
в противном случае; |
|||||
|
|
|
|
|
|||||||
в) в мультиграфе ai Пример. Для графа
v1
e7
e8
v6
e9
v4
, j = k, где k – кратность ребра (vi vj). изображенного на рисунке
e1 |
v2 |
|
|
|
|
|
e3 |
e4 |
e2 |
|
v3 |
e5
v5
e6
матрица смежности имеет вид
|
0 |
1 |
0 |
0 |
1 |
1 |
||
|
|
1 |
0 |
1 |
0 |
1 |
1 |
|
|
|
|
||||||
|
|
0 |
1 |
0 |
1 |
0 |
0 |
|
A |
|
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
1 |
1 |
|||
|
|
1 |
1 |
0 |
1 |
0 |
0 |
|
|
|
|
||||||
|
|
1 |
1 |
0 |
1 |
0 |
0 |
|
|
|
|
||||||
|
|
|
|
|
10 |
|
|
|
Свойства матрицы смежности: Матрица смежности неориентированного графа является симметричной относительно главной диагонали. Диагональные элементы этой матрицы указывают на наличие петель в соответствующем графе.
Сумма элементов матрицы А неориентированного графа по i-ой строке (или i-му столбцу) равна d(vi). Для ориентированного графа сумма элементов матрицы А по i-ой строке рав-
на d |
|
(vi), а по j-му столбцу d |
|
( vj). |
|
|
Графы изоморфны тогда и только тогда, когда их матрицы смежности получаются друг из друга одновременной перестановкой строк и столбцов (i, j строк и i, j столбцов).
Объём памяти для матрицы смежности – О(n2) Матрицей инцидентности графа G=(V, E) с n вершина-
ми и m ребрами называется матрица В размера n×m, элементы которой определяются следующим образом:
а) для неориентированного графа
b |
|
1, |
если вершина v инцидентна ребруe |
, |
||
|
|
i |
j |
|
||
|
|
|
|
|||
i, j |
|
0 |
- |
в противном случае. |
||
|
|
|
||||
б) для ориентированного графа
|
|
1, если вершина v |
является началом дугиe |
, |
||||
|
|
|
|
i |
|
j |
|
|
b |
|
1, |
если вершина v служит концом дугиe |
, |
||||
|
||||||||
i, j |
|
|
|
i |
j |
|
||
|
|
|
0, |
если вершина v не инцидентна дугеe |
. |
|||
|
|
|
||||||
|
|
|
|
i |
j |
|
||
Например, для графа предыдущего примера:
|
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
||
|
|
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
|
|
|
|||||||||
|
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
B |
|
|
|
|
|
|
|
|
|
|
|
0 0 0 0 1 |
1 |
0 |
0 |
1 |
|||||||
|
|
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
|
|
|
|||||||||
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
|
|
|
|||||||||
Заметим, что мультиграфы изоморфны тогда и только тогда, когда их матрицы инцидентности получаются друг из друга некоторыми перестановками строк или столбцов.
Объём памяти для матрицы инцидентности – О(nm)
11

2.2. Список ребер (дуг) и структура смежности графа.
Если граф является разреженным, то есть когда число
рёбер (дуг) m= |
E |
много меньше числа вершин n= V |
, то целе- |
|
|
|
|
сообразно представлять граф посредством списка рёбер (дуг).
Этот список задается двумя наборами |
v (v |
, v |
2 |
,...,v |
m |
) |
и |
|
1 |
|
|
|
|
||
u (u1, u2,...,um ) , где (vi , ui ) - i-ая дуга графа. |
|
|
|
|
|
||
Пример. Для графа, приведенного ранее, имеем:
v (1,1,2,2,3,4,1,2,4) и u (2,5,5,3,4,5,6,6,6) . Здесь для упроще-
ния записи мы пишем 1 вместо a1 , 2 - вместо a2 и т.д.
Объём памяти для списка рёбер (дуг) – О(2m) Представлением графа, удобным при операциях с гра-
фами, в которых добавляются или удаляются вершины, является структура смежности. Она получается путем составления
для каждой вершины |
a V |
списка номеров вершин |
b V |
, |
|
для которых (a, b) E . |
|
|
|
||
Пример. Для графа, представленного ранее, имеем: |
|
|
|||
|
|
|
|
|
|
Вершины |
|
Список последовательностей |
|
|
|
1 |
|
|
2,5,7 |
|
|
2 |
|
|
1,3,5,6 |
|
|
3 |
|
|
2,4 |
|
|
4 |
|
|
3,5,6 |
|
|
5 |
|
|
1,2,4 |
|
|
6 |
|
|
1,2,4 |
|
|
Объём памяти для структуры смежности – О(n+m)
2.3. Части графов.
G
Подграфом графа |
G (V , E) |
(V , E ) , для которого V V и E |
|
называется граф
E .
Полный подграф некоторого графа называется кликой этого графа.
12
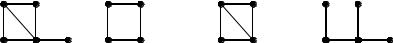
|
Остовным подграфом графа |
G (V , E) |
называется под- |
граф, содержащий все вершины |
исходного |
графа G, т.е. |
|
Go |
(V , Eo ) , где Eo E . |
|
|
|
Порожденным подграфом графа G (V , E) на множе- |
||
стве вершин Vp называется граф Gp=(Vp, Ep), причем Vp V ,а Ep – множество ребер или дуг графа G, оба конца которых принадлежат множеству Vp.
Пример. На следующем рисунке изображены:
а) - исходный граф G, б) - один из его подграфов, в) - порож- |
||||||||||
дённый подграф графа G на множестве вершин |
v1,v2 |
,v3 |
,v4 , |
|||||||
г) – один из остовных подграфов графа G. |
|
|
|
|
|
|||||
v |
v |
|
v |
v |
v |
v |
v |
v |
3 |
|
2 |
3 |
|
2 |
3 |
2 |
3 |
2 |
|
|
|
|
v |
v |
|
v |
|
v |
|
v |
4 |
v |
v |
4 |
5 |
v |
4 |
v |
4 |
v |
|
5 |
|
|
|
|
|
|
|
|
||||
1 |
|
|
1 |
|
1 |
|
1 |
|
|
|
|
а) |
|
|
б) |
в) |
|
г) |
|
|
|
2.4. Основные операции над графами.
Объединением графов G1=(V1, E1) и G2=(V2, E2) называется граф G3=(V1 V2, E1 E2). Объединение называется дизъюнктным , если V1 V2=0.
Пересечение графов G1=(V1, E1) и G2=(V2, E2) называется
граф G3=(V1 V2, E1 E2).
Аналогично определяются объединение, дизъюнктное объединение и пересечение любого количества графов. Операции объединения и пересечения являются коммутативными,
т.е. G1 G2= G2 G1, а также G1 G2= G2 G1
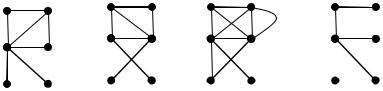
Пример. На ниже приведённом рисунке показаны: а) – граф G1, б) – граф G2, в) – их объединение, г) – пересечение.
13
|
|
|
|
|
|
|
|
|
|
|
e1 |
v1 |
e1 v2 |
v1 |
|
e1 |
v2 |
v1 |
e1 |
v2 |
v1 |
v2 |
|
e5 |
e4 e2 |
|
e5 |
e9 |
e8 |
e5 e9 |
e8 e2 |
e5 |
v4 |
||
v3 |
e3 |
|
v3 |
|
e3 |
v4 |
v3 |
e3 |
v4 |
v3 |
e3 |
v4 |
e10 |
e6 |
|
e7 |
e6 |
|
|
e6 |
|||
e7 |
e6 |
|
|
|
|||||||
v6 |
v5 |
|
|
v6 |
v5 |
e10 |
v6 |
v5 |
v6 |
||
v5 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||
|
а) |
|
|
|
б) |
|
|
в) |
|
|
г) |
|
|
|
|
|
|
|
|
|
|
|
|
Удаление вершины. При удалении вершины из графа удаляются и все инцидентные ей рёбра (дуги).
Удаление ребра (дуги). При удалении ребра (дуги) его концевые вершины не удаляются. Операцией обратной к операции удаления ребра является операция добавления ребра.
Слияние (отождествление) вершин. Говорят, что вершины vi и vj в графе G отождествляются (сливаются) если они заменяются новой вершиной vk такой, что все ребра (дуги) графа инцидентные vi и vj становятся инцидентными к вершине
vk .
Стягивание ребра – эта операция означает удаление ребра и отождествление его концевых вершин. Граф G называется стягиваемым графу Н, если граф Н может быть получен из G в результате некоторой последовательности стягиваний ребер.
Подразбиение ребра. При выполнении этой операции из графа удаляется ребро (vi, vj) и добавляются два новых (vi, vk) и (vk, vi), где vk – новая вершина графа.
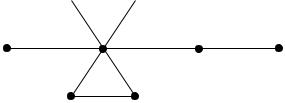
Пример:
На следующем рисунке представлены: а) - исходный граф, б) – граф после удаления вершины v3, в) - результат удаления ребра e2, г) –отождествления вершин v3 и v4, д) – стягивание ребра e1, е) – подразбиение ребра e2.
14

v3 |
e1 |
|
v4 |
|
|
e2 |
|
e3 |
|
e4 |
|
|
|
e5 |
|
|
|
v1 |
а) |
|
v2 |
v1 |
|
|
|
|
|
|
|
v5 |
e1 |
|
|
v5 |
|
|
|
|
|
|
|
e2 |
e3 |
e4 |
e2 |
||
e5 |
|
|
|||
|
|
|
|
|
|
v1 |
г) |
|
v2 |
v1 |
|
|
|
|
|
|
|
v4
e3 e4 e5
б) v2
e3 e4 e5
д) v2
15
v3
v1
v3
e8
v6
e7 v1
e1
e3
e5
в) e1
e3
e5
е)
v4
e4
v2
v4
e4
v2
3. МАРШРУТЫ В ГРАФАХ.
3.1. Понятие маршрута.
Маршрутом в графе G=(V,E) называется чередующаяся последовательность вершин и ребер (дуг) – v1, e1, v2, e2, …., vn, en,vn+1, в которой любые два соседних элемента инциденты.
Маршрут, соединяющий вершины v1 и vn+1 можно также задать последовательностью из одних вершин v1, v2, v3,…,vn, vn+1 или последовательностью ребер e1, e2,…,en. Число n ребер (или дуг) в маршруте называется его длиной. Маршрут называется циклическим, если v1=vn+1.
Маршруты в неориентированных графах.
Маршрут в неорграфе называется цепью, если все его ребра различны. Цепь называется простой, если все её вершины, кроме возможно первой и последней, различны. Циклическая цепь называется циклом, а простая циклическая цепь – простым циклом.
Неорграф без циклов называется ациклическим графом. Минимальная из длин циклов неорграфа называется его обхватом.
Пример 1: Рассмотрим неорграф
1  2
2
3 |
4 |
5 |
6 |
7 8
В данном примере наборы вершин: (1,2) ; (1,2,4,7) являются простыми цепями,: (1,2,4,7,8,4) - непростая цепь, (1,2,4,7,8,4,2) – маршрут, который не является цепью, (1,2,4,8,7,4,1) – непростой цикл, (1,2,4,1) – простой цикл. Об-
хват графа равен 3.
16

Маршруты в ориентированных графах.
Маршрут ориентированного графа называется путем, если все его дуги различны.
Путь называется контуром, если v1=vn+1. Граф не имеющий контуров называется безконтурным. Вершина v называется достижимой из вершины u, если существует путь из u в v.
Пример 2: Рассмотрим ориентированный граф
2
4 5
13
Вданном примере наборы вершин (1,2,3,1) образуют контур. Заметим, что здесь вершина 5 – достигается из любой другой вершины, а из вершины 5 не достигается ни одна из остальных вершин.
3.2. Связность в графах.
Неорграф называется связным, если любые две его несовпадающие вершины соединены маршрутом. Граф называется связным, если соответствующий ему неорграф является связным. В данном случае соответствующий неориентированный граф получается из исходного графа путём замены всех его дуг рёбрами. Граф называется сильно связным, если для каждой пары различных вершин u и v существуют маршруты (u,v) и (v,u). Из этого определения следует, что любой связный неорграф является также сильно связным. Понятия связности и сильной связности распространяются также и на мультиграфы.
Отметим, что граф в примере 1 является сильно связным, а в приме2 – не сильно связный граф.
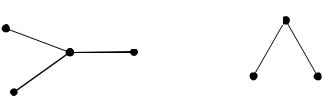
Пример 3. На следующем рисунке показан несвязный
граф.
17
2
6
3 4
5  7
7
1
Всякий максимальный по включению сильно связный подграф данного графа называется его сильно связной компонентой, или сильной компонентой связности.
В примере 3 граф имеет две сильно связных компонен-
ты.
3.3. Связность и матрица смежности графа.
Теорема 1. Любой граф представляется в виде объединения непересекающихся (сильно) связных компонент. Разложение графа на (сильно) связные компоненты определяется однозначно.
Таким образом, множество вершин связных компонент, а также сильных компонент образуют разбиение множества вершин графа, причем число с(G) связных компонент графа G определяется однозначно.
Теорема 2. Если A матрица смежности графа G, то (i, j) элемент матрицы Ak=A·A·A··…·A (k раз), есть число (vi, vj) маршрутов длины k.
Следствие 1. В графе G мощности n тогда и только тогда существует маршрут (vi, vj) , причем vi ≠vj , когда (i, j) – элемент матрицы A+A2+ A3+ A4+…+ An-1 не равен нулю.
Следствие 2. В графе G мощности n тогда и только тогда существует цикл, содержащий вершину vi когда (i, i) – элемент матрицы A+A2+ A3+ A4+…+ An-1+An не равен нулю.
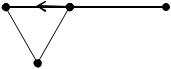
Пример. При помощи матрицы смежности определим существование всевозможных (1, 3) - маршрутов в графе, изображенном на рисунке.
18
1 |
2 |
3 |
4
По графу находим матрицу смежности A:
0 |
0 |
0 |
1 |
|
||
|
1 |
0 |
1 |
1 |
|
|
|
|
|||||
A= |
0 |
1 |
0 |
0 |
. |
|
|
|
|||||
|
|
|
|
|||
|
1 |
1 |
0 |
0 |
|
|
|
|
|||||
Её элемент (1,3)=0, следовательно. (1, 3) маршрутов длины 1 в графе нет. Затем находим:
|
0 |
0 |
0 |
1 |
|
0 |
0 |
||||
|
|
1 |
0 |
1 |
1 |
|
|
|
1 |
0 |
|
A2= |
|
|
. |
|
|||||||
|
0 |
1 |
0 |
0 |
|
|
0 |
1 |
|||
|
|
||||||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||
|
|
1 |
1 |
0 |
0 |
|
|
|
1 |
1 |
|
|
|
|
|
|
|||||||
В этой матрице элемент длины 2 в графе нет. Далее
1 |
1 |
0 |
0 |
0 |
0 |
||||
|
1 |
2 |
0 |
1 |
|
|
1 |
0 |
|
|
|
|
|||||||
A3= A2·A = |
1 |
0 |
1 |
1 |
|
· |
0 |
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
||||
|
1 |
0 |
1 |
2 |
|
|
1 |
1 |
|
|
|
|
|||||||
0 |
1 |
1 |
1 |
0 |
0 |
|
|||
1 |
1 |
|
|
1 |
2 |
0 |
1 |
|
|
|
|
|
|||||||
0 |
0 |
|
= |
1 |
0 |
1 |
1 |
. |
|
|
|
|
|||||||
|
|
|
|
|
|
||||
0 |
0 |
|
|
1 |
0 |
1 |
2 |
|
|
|
|
|
|||||||
(1,3)=0, т.е. (1, 3) маршрута
0 |
1 |
1 |
0 |
1 |
2 |
||||
1 |
1 |
|
|
3 |
1 |
2 |
3 |
|
|
|
|
|
|||||||
0 |
0 |
|
= |
1 |
2 |
0 |
1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
||||
0 |
0 |
|
|
2 |
3 |
0 |
1 |
|
|
|
|
|
|||||||
Eё элемент (1, 3)=1, т.е. существует ровно один (1, 3) - маршрут длины 3. Этот маршрут определяется набором вершин (1,
4, 2, 3)
Эту последовательность вершин можно найти на основе перемножения матрицы смежности: Элемент (1, 3) матрицы A3 получается при перемножении элемента (1, 2) матрицы A2 на элемент (2, 3) матрицы A. В свою очередь элемент (1, 2) мат-
19
