
Теория графов
.pdf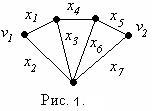
16. ПЕРЕКЛЮЧАТЕЛЬНЫЕ СЕТИ (СХЕМЫ).
Рассмотрим граф без петель G=(V,E), каждому ребру еi которого поставлена в соответствие переменная xi , принимающая значение только 0 или 1. Такой граф может считаться математической моделью множества взаимосвязанных физических устройств, например ключей, каждый из которых может быть в любом из двух состояний: включенном (xi=1) или выключенном (xi=0). Пусть v1 и v2 – две различные фиксированные вершины G. Исходный граф вместе с переменными {xi} называется переключательной схемой (сетью), а v1 и v2 считаются её конечными точками (терминалами).
Если в сети существует n ребер (т.е. ключей) и Х=(x1,x2,…,xn) есть некоторая комбинация значений переменных, то рассматриваемая сеть будет замкнутой относительно Х тогда и только тогда, когда множество ребер, для которых xi=1, образует элементарную сеть, соединяющую v1 и v2 . В противном случае говорят, что сеть замкнута относительно Х. (Другими словами, сеть замкнута относительно Х тогда и только тогда, когда v1 и v2 лежат в одной и той же компоненте подграфа, определённого ребрами, для которых xi=1).
Рассмотрим, например, переключательную сеть рис. 1. Множество переменных переключения, соответствующих элементарным
цепям, соединяющим v1 и v2 , есть
((1,4,5), (1,4,6,7), (1,3,6,5), (1,3,7),
(2,7), (2,6,5), (2,3,4,5)), где цифры совпадают с индексами переменных. Векторы Х=(x1,x2,…,x7), для которых
сеть замкнута являются в точности теми векторами, которые имеют 1 в каждой позиции, соответствующей одной из элементарных цепей, и произвольные значения в других позициях.
Переключательная функция f(X) данной переключательной сети N с n ключами определяется на 2n возможных значениях Х следующим образом:
90
1, |
если N замкнута относитель но Х, |
f ( X ) |
в противном случае. |
0, |
|
|
|
от xj
До сих при i j
пор мы неявно предполагали, что xi не зависит , т.е. что все n ключей управляются независимо
друг от друга. Если это не так, то не все 2n значений Х являются допустимыми. Предположим, что в предыдущем примере
x7 x1 и |
x6 x2 , |
x2 1 x2 . |
Тогда цепь, определяемая индексами (2,6,5), не может быть замкнутой, так как x2 и x6 не могут быть одновременно равны 1. Аналогично цепь (1,3,7) замкнута всякий раз, когда
x1=x3=1,
так как в этом случае мы обязательно имеем x7=1.
Возникает следующая общая задача. Сформулировать условия, при которых может быть найдена переключательная сеть, реализующая заданную переключательную функцию f(X) от m независимых переменных (x1,…,xm).
Любая переключательная функция может быть реализована достаточно большой сетью, каждая переменная которой равна одной из m независимых переключательных переменных или её дополнению. Например, если m=3 и f(X)=1 для следующих значений Х:
|
x1 |
x2 |
x3 |
X1 |
1 |
0 |
1 |
X2 |
1 |
1 |
0 |
X3 |
0 |
1 |
1 |
X4 |
0 |
0 |
1 |
то сеть рис. 2, очевидно, реализует заданную переключательную функцию. К сожалению, высокая степень избыточности, возникающая при таком способе построения цепи, как правило, недопустима.
91
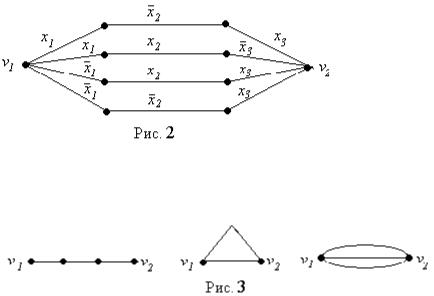
Естественно стремиться использовать наименьшее количество ключей (в лучшем случае m). В предыдущем примере, при m=3, существует только три различных представляющих интерес конфигурации, которые показаны на рис. 3.
Они не обеспечивают достаточного разнообразия структур для реализации всех 28 возможных переключательных функций при сравнительно небольшом числе ключей. Например, в работе [64] для решения этой задачи используются свойства фундаментального цикла и матриц разрезов, рассмотренные в главе 5. Показано, что задача реализуемости переключательной функции связана с задачей реализуемости матрицы циклов соответствующего графа с помощью заданной матрицы.
92
17. МАТЕМАТИЧЕСКИЕ МАШИНЫ И ЦЕПИ МАРКОВА
Многие реальные системы можно характеризовать, выделяя различные состояния, в которых они могут находиться, и задавая их реакции на поступление произвольных входных воздействий при нахождении систем в любом заданном состоянии. Как правило, реакция системы проявляется в форме перехода из одного состояния в другое и формировании соответствующего выходного сигнала. Формализация предыдущей идеи приводит к понятию математической машины.
Последние работы по теории математических машин (называемой иногда теорией автоматов) как будто бы имеют мало общего с глубокими исследованиями Гёделя, Тьюринга и других специалистов по математической логике.
Новые теории в основном опираются на элементарные теоремы, но, тем не менее, приводят к трудным комбинаторным задачам, которые, вероятно, удобно решать методами теории графов.
Определение. Машина есть математическая система, которая состоит из
1)конечного множества S={s1,…, sm} элементов, называемых состояниями,
2) |
конечного множества |
X={x1,…, xn} элементов, |
|
называемых входами, |
|
3) |
конечного множества |
Y={y1,…, yk} элементов, |
|
называемых выходами, |
|
4)функции перехода Т, которая отображает S×X на S,
5)функции выхода Ω, которая отображает S×X на Y,
Если s принадлежит S и x принадлежит X, то s`=Т(s,x) интерпретируется как следующее состояние, в которое попадает машина из текущего состояния s при воздействии входного сигнала x. Множества X и Y называются соответственно входным и выходным алфавитом (хотя, природа их элементов существенно изменяется в зависимости от рассматриваемых задач).
93
Машины, соответствующие данному определению, можно классифицировать по нескольким признакам. Вопервых, они являются детерминированными, так как их выходной сигнал и следующее состояние полностью определяются входным сигналом и текущим состоянием. Во-вторых, такие машины являются последовательностными, так как входные сигналы подаются в дискретные моменты времени t1, t2, t3, а не непрерывно. Они являются полными, т.е. каждая комбинация состояния и входного сигнала (входа) имеет смысл и дает известный выходной сигнал (выход) и новое состояние. Они не имеют памяти в том смысле, что текущий выход и следующее состояние не зависят от прошлых входов, состояний или выходов. Наконец, они стационарны в том смысле, что функция переходов Т и функция выхода Ω не зависят от рассматриваемого момента времени. Изменив некоторые или все из названных предположений, можно получить определение машины более общего вида.
Иногда машину удобно изображать ориентированным графом, вершины которого соответствуют состояниям, а дуги характеризуют X,Y,T и Ω.
Сказанное проще всего пояснить на примере. Рассмотрим машину для которой
S={s1, s2, s3, s4}, X={0,1} и Y={a,b,c}.
Одна из возможных машин с множеством состояний S и алфавитами X и Y представлена в виде графа рис. 1.
94
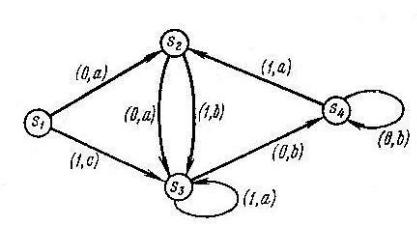
Рис. 1.
Каждая вершина соответствует одному состоянию. Начальная вершина инцидентна точно двум дугам (в общем случае к дугам, где к – число различных входов). Если некоторая дуга идет из вершины s в вершину s` и ей соответствует упорядоченная пара (x, y), то T(s, x)=s`, (s, x)=y. Например, если текущее состояние s3, то вход 0 даст выход b и переведет систему в состояние s4. С другой стороны, вход 1 дает a и система останется в состоянии s3. (Практически число дуг можно уменьшить, помечая некоторые дуги несколькими упорядоченными парами, если несколько входов дают одно и то же следующее состояние.)
Отдельные состояния и множества можно классифицировать по структурным признакам соответствующего графа. Например, машина называется сильно связной, если ей соответствует сильно связный граф. Независимо от начального состояния s такую машину можно всегда перевести в любое другое состояние s` с помощью соответствующей последовательности входов (не обязательно за один шаг). Состояние s называется переходным, если из соответствующей ему вершины выходит, по крайней мере, одна дуга (s, t), где t s, и если эта вершина не является конечной ни для одной дуги (u, s), где u s. Например, s1 – переходное соcтояние. Состояние s1, кото-
95
рому соответствует вершина, являющаяся конечной, по крайней мере, для одной дуги (t, s), где t s, и не являющаяся начальной ни для одной дуги (s, u) где s u, называется устойчивым. (Рассматриваемая машина не имеет отдельных устойчивых состояний. Однако состояние s2, s3 и s4 совместно образует в соответствующем смысле устойчивое множество состояний).
При заданном начальном состоянии s и произвольной ленте или конечной последовательности входов с помощью графа можно легко определить результирующее конечное состояние s` (после t переходов) и соответствующую выходную последовательность y1,…,yt. Например, если в текущий момент машина находиться в состоянии s1 и следующие пять входов равны 1, 1, 0, 1, 0, то она последовательно перейдет в состояние s3, s3, s4, s2, s3 и выходные сигналы будут равны c, a, b, a, a.
Отметим следующие классы задач, существующие в теории абстрактных машин.
1.Анализ реакции (переходов и выходов) заданной машины.
2.Синтез машины с заданными характеристиками реакций.
3.Приведение машины к более простой в некотором смысле эквивалентной форме.
Более подробное рассмотрение вопросов, связанных с теорией абстрактных машин, читатель может найти в работах Жилля и Гинзбурга. В данном случае нам хотелось лишь подчеркнуть, что одним из удобных способов представления таких машин являются ориентированные графы с соответствующей символикой. В частности, их удобно использовать для классификации машин и некоторых видов их анализа.
Идея марковской цепи в некотором смысле является вероятностным аналогом абстрактных детерминированных машин. Здесь снова мы имеем систему, которая может находиться в одном из конечного числа состояний и изменять состояния в дискретные моменты времени. Однако при этом переходы не
96
зависят от управляемых входов, а определяются распределениями вероятностей. Выходные переменные в данном случае отсутствуют. Наибольший интерес в такой модели представляет распределение вероятностей состояний как функция времени при заданном начальном состоянии.
Цепь Маркова формально можно определить как систему, которая состоит из:
1)конечного множества S={s1,…,sn} элементов, называемых состояниями,
2)n n – матрицы переходов P={piJ}, где piJ – вероятность того, что в следующий момент наблюдения система будет находиться в состоянии sj при условии, что в текущий момент она находиться в состоянии si. Конечно, требуется, чтобы выполнялось соотношение
pij |
1 |
i |
|
(I = 1,2,…,n).
Определенная таким образом цепь Маркова называется иногда стационарной (или независящей от времени), в отличии от цепи Маркова более общего вида, в которой вероятности переходов могут быть функциями времени.
Цепи Маркова соответствует ориентированный граф. Вершины графа определяются состояниями цепи. Каждой дуге из si в sj поставлено в соответствие число pij в случае pij>0 (т. е. в случае, когда возможен одношаговый переход из si в sj). Граф цепи Маркова с пятью состояниями показан на рисунке 2. Если текущее состояние системы s2, то она переходит в состояние s3, s5 или остается в s2 с вероятностями 0,2; 0,3 и 0,5 соответственно. Другие дуги интерпретируются аналогично.
Качественную классификацию состояний или множеств состояний можно провести на основе структурных свойств графа без учета конкретных значений вероятностей (различаются только нулевые и ненулевые вероятности). Например, множество состояний Т S называется поглощающим, если ориентированный разрез {T, S-T} является пустым
97

Рис. 2.
(т.е. из состояний в множестве Т нельзя попасть ни в какие другие состояния, не принадлежащие Т). В частности, отдельное состояние является поглощающим тогда и только тогда, когда pij = 1. Цепь Маркова называется эргодической, если соответствующий граф сильно связан. Таким образом, эргодическая цепь это такая цепь, для которой при любом текущем состоянии si существует ненулевая вероятность достижения любого другого
Рис. 3.
состояния за соответствующее число шагов (переходов). Эргодическая цепь называется регулярной, если существует по-
98
ложительное целое число t0 такое, что для любых состояний si и sj ( возможно i=j ) есть путь из vi в vj, имеющий в точности t дуг для всех t t0. Цепь на рис. 3, а, например, является эргодической, но нерегулярной. (Действительно, если начать, скажем, с s1, то можно оказаться в s3 только после четного числа шагов). В отличии от неё, цепь рис. 3, b регулярна.
99
