Вектор называется нулевым, если начало и конец его совпадают. Нулевой вектор не имеет определенного направления и имеет длину, равную нулю.

Определение. Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.

Определение. Два вектора называются равными, если они коллинеарные, имеют одинаковую длину и одинаковые направления. (Все нулевые векторы равны).

Определение. Векторы называют компланарными, если они лежат либо

водной плоскости, либо в параллельных плоскостях.

4.2.Линейные операции над векторами. Проекция вектора на ось

1. Операция сложения;

2. Операция вычитания (частный случай сложения);

3. Операция умножения на вещественное число.

Вдальнейшем нам потребуются понятия: проекция вектора на ось и угол наклона вектора. Введем эти понятия.

В

А

А/ В/ и

Рис. 2

.

16

Если координаты точек начала и конца вектора A(x1, y1, z1) ; B(x2 , y2 , z2 ) ,

4.3. Линейная зависимость и линейная независимость векторов на плоскости и в пространстве

сумму произведений этих векторов на произвольные вещественные числа, т.е.

где 1, 2 , ... n - любые вещественные числа.

если найдутся такие вещественные числа 1, 2 , ... n , из которых хотя бы одно

независимыми, если равенство нулю их линейной комбинации (4.1) возможно

нулевым, то эти векторы линейно зависимы.

Теорема. Если среди n векторов какие-либо (n-1) векторы линейно зависимы, то все n векторов линейно зависимы.

Теорема. Необходимым и достаточным условием линейной зависимости двух векторов является их коллинеарность.

Следствие 1. Если векторы a и b не коллинеарны, то они линейно независимы.

Следствие 2. Среди двух линейно независимых векторов не может быть нулевого вектора (иначе они оказались бы линейно зависимыми).

Теорема. Необходимым и достаточным условием линейной зависимости трех векторов является их компланарность.

Определение. Линейное пространство R называется n-мерным, если в нем существует n линейно независимых векторов, а любые из (n+1) векторов уже являются зависимыми, то есть размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов.

17

4.4. Базис на плоскости и в пространстве

Справедливы следующие утверждения:

1.Любая тройка некомпланарных векторов a , b и c образует базис в пространстве.

2.Любая пара лежащих на плоскости неколлинеарных векторов a и b образуют базис на этой плоскости.

3. Каждый вектор d может быть единственным способом разложен по

В чем необходимость базиса?

При задании базиса линейные операции над векторами становятся обычными линейными операциями над числами-координатами этих векторов, а именно:

d на любое число все его координаты умножаются на это число.

Тогда в силу свойств линейных операций над векторами:

4.5. Переход к новому базису

Пусть в пространстве R имеются два базиса: старый

и новый , ,…, . Каждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса:

(4.5)

Найдем зависимость между координатами вектора в разных базисах.

то есть в матричной форме

Здесь

–

матрица перехода, причем коэффициенты разложения новых базисных векторов по старому базису образуют столбцы этой матрицы.

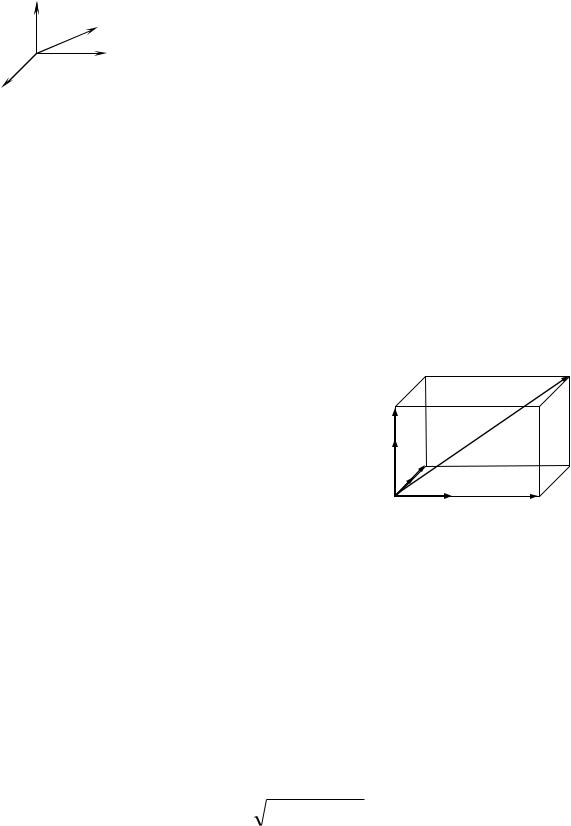
4.6. Декартова прямоугольная система координат

Реальное пространство, которое мы будем изучать, называется трехмерным R3. Каждая точка в нем определяется тройкой действительных чисел. Плоскость – R2.

Определение. Декартова прямоугольная система координат

представляет собой три взаимно перпендикулярные оси в пространстве с общим началом О и одинаковой масштабной единицей:

19