ГОУВПО "Воронежский государственный

технический университет"

Кафедра "Экономика, производственный менеджмент и

организация машиностроительного производства"

223-2008

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по выполнению самостоятельной работы и

индивидуальных заданий по дисциплине

"Разработка производственных управленческих решений"

для студентов специальностей 080502

«Экономика и управление на предприятии» и

080500 «Менеджмент» очной формы обучения

Воронеж 2008

Составитель: д-р экон. наук С.В. Амелин

УДК 519.85

Методические указания по выполнению самостоятельной работы и индивидуальных заданий по дисциплине "Разработка производственных управленческих решений" для студентов специальностей 080502 "Экономика и управление на предприятии" и 080500 "Менеджмент" очной формы обучения / ГОУВПО "Воронежский государственный технический университет"; сост. С.В. Амелин. Воронеж, 2008. 47 с.

Разработка и принятие оптимальных управленческих решений в современных условиях не обходится без информационно-математической поддержки, проведения многовариантных расчетов на основе использования экономико-математических методов и моделей. В работе представлена программа курса, вопросы для самостоятельного изучения материала, рекомендуемые литературные источники, а также приведены варианты для выполнения индивидуальных заданий.

Табл. 4 . Ил. 8 . Библиогр.: 19 назв.

Рецензент канд. экон. наук, доц. Г.Н. Чернышова

Ответственный за выпуск зав. кафедрой д-р экон. наук, проф. О.Г. Туровец

Печатается по решению редакционно-издательского совета Воронежского государственного технического университета

_© ГОУВПО "Воронежский государственный технический

университет", 2008

ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Студенты должны ознакомиться с программой и содержанием основных вопросов по дисциплине “Разработка производственных управленческих решений”, внимательно изучить соответствующие методические указания и решение типовых задач.

В процессе изучения дисциплины студенты отвечают на вопросы для самопроверки. Выполняя индивидуальные задания, студенты должны показать ход решения, подробно изложить расчеты, расшифровать все используемые формулы, сделать краткие выводы.

Изучая дисциплину “Разработка производственных управленческих решений”, студенты выполняют тот вариант задания, номер которого соответствует номеру студента по списку группы. Таблицы соответствия вариантов заданий номерам групп и номерам в списке необходимо получить у преподавателя. Перед решением задачи необходимо ознакомиться с теоретическим материалом, соответствующего раздела дисциплины “Разработка производственных управленческих решений ”.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Чем вызывается необходимость принятия решений?

2. Чем отличается принятие управленческих решений от частного выбора?

3. Какие аспекты управленческого решения выделяют его исследователи?

4. Назовите основные виды управленческих решений.

5. Охарактеризуйте возможные условия, в которых менеджеру приходится принимать решения: определенность, риск, неопределенность.

6. Какие решения называются формализованными и в чем заключаются их преимущества?

7. Что понимается под «качеством» управленческого решения?

8. Какими факторами обеспечивается научная обоснованность управленческого решения?

9. Какие личные качества необходимы менеджеру для успешного принятия решений?

10. Что называется процессом принятия решений и каковы его основные этапы?

11. Дайте понятие проблемы.

12. Что понимается под критериями выбора?

13. Какое решение можно считать оптимальным?

14. Чем вызывается необходимость согласования решений?

15. Опишите процедуру принятия решений в японской

модели управления. Дайте сравнительный анализ системы «ринги» и западной модели принятия решений.

16. В каких ситуациях и какие математические модели могут помочь менеджеру в разработке и принятии решений?

17. Назовите основные этапы процедуры разработки оптимизации решения методами моделирования.

18. В каких случаях целесообразно использование экспертных технологий в процессах принятия решений?

19. Назовите основные методы экспертных оценок.

20. В чем заключается сущность метода мозговой атаки?

21. Какие особенности проведения экспертизы присущи методу Дельфи?

22. Кого можно считать экспертом? Охарактеризуйте основные способы, используемые для оценки качеств экспертов.

23. Назовите основные типы шкал, применяемых для количественных измерений. Какие шкалы применяются экспертами для получения качественных оценок?

24. Что понимается под интеллектуальными системами и каково их назначение? Что представляет собой СППР?

25. Дайте определение понятия «риск». Должен ли менеджер избегать риска?

26. Рассмотрите основные виды рисков. Как можно количественно оценить уровень риска?

27. Назовите основные элементы механизма реализации решений.

28. Для чего необходима стадия контроля и оценки результатов решения?

29. Чем определяется вид ответственности руководителя за принятое решение? Назовите виды юридической ответственности.

30. Как в организации реализуется административная ответственность?

31. Чем различаются дисциплинарная и материальная ответственность?

32. Какими факторами определяется эффективность управленческого решения?

Задание № 1

ПРИНЯТИЕ РЕШЕНИЙ

В УСЛОВИЯХ МНОГОКРИТЕРИАЛЬНОСТИ

МНОЖЕСТВО ПАРЕТО

Важное понятие теории принятия управленческих решений - понятие «цели». Цель - это желаемый результат деятельности.

Результат принятого решения стараются описать функцией, аргументами которой являются разные варианты решений, а значениями числа, отражающие меру достижения цели. Эту функцию называют целевой функцией, или критерием, а лучшим будет то решение, которое делает значение целевой функции большим или меньшим (исходя из ее смысла).

Среди вариантов решений только некоторые удовлетворяют ограничениям, не нарушают их. Такие решения называются допустимыми, допустимое решение, которое доставляет максимум (или минимум) целевой функции, называется оптимальным.

В дальнейшем будем использовать такие обозначения:

F(х) - целевая функция скалярного или векторного аргументах; Х - допустимое множество;хХ- имеет обычный смысл (хпринадлежит Х, является одним из элементов Х);

G(х) ≤ 0, …,Q(х) ≤ 0 - функциональные ограничения, описывающие взаимосвязи переменных.

Найти то значение переменной, которое доставляет экстремум (максимум или минимум) целевой функции, и величину целевой функции при этом значении означает решить данную оптимизационную задачу. В стандартной форме оптимизационную задачу максимизации можно записать, например, так:

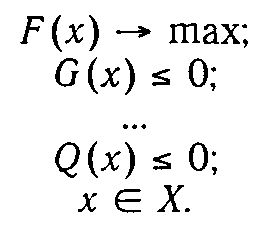
В силу экономического смысла переменных хот них очень часто требуется неотрицательность. В некоторых случаях с помощью искусственного добавления переменных функциональные неравенства можно превращать в уравнения.

Оптимальное решение может быть не единственным или отсутствовать. Если оптимальное решение - не единственное, то есть существуют несколько решений, которые доставляют экстремум целевой функции, то значение целевой функции для всех этих решений одно и то же (рис. 1). Решение оптимальное по одному критерию, может не быть оптимальным по другому критерию.

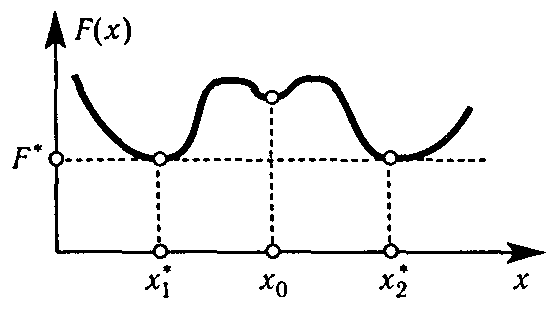
Рис. 1. Два оптимальных решения задачи F(х) →min,х ≥ 0.

х₁^*, х₂^*- оптимальные решения, х₀- не оптимальное решение.F(х₁) =F(х₂).

Напомним еще смысл двух распространенных терминов: эффект это результат деятельности, эффективность - это со- измерение результата и затрат.

Основные этапы работы с оптимизационными задачами:

1. Постановка задачи, то есть ее содержательная формулировка с точки зрения и заказчика, и разработчика.

2. Построение математической модели, то есть переход к формализованному представлению, общий вид которого приведен выше.

3. Нахождение решения или решений (нахождение какого-либо решения или всех оптимальных и близких к нему решений - это разные задачи и по постановке, и по методам, и по сложности, и по результативности полу чаемых вариантов).

4. Проверка модели и полученного с ее помощью решения. Это - необходимый этап, так как модель лишь частично отображает действительность. Хорошая модель должна точно предсказывать влияние изменений в реальной системе на общую эффективность решений.

5. Построение процедуры подстройки модели, поскольку в модели могут изменяться какие-либо неуправляемые переменные.

6. Выбор вариантов, если есть несколько конкурирующих вариантов.

7. Осуществление решения.

Как правило, перечисленные этапы перекрываются, идут параллельно или несколько раз циклически повторяются.

Пусть есть несколько целевых функций F₁(), …,F₂(), каждую из которых хотят максимизировать.

Вектор решения ^* называют эффективным, если не существует другого вектора’, для которого значения всех функцийF_i (’)≥F_i (^*) и хотя бы одно неравенство - строгое. Суть в том, что есть несколько (эффективных) решений, которые несравнимы: одно решение в чем-то лучше по одному из критериев, но хуже по другому, и нет такого вектора, который был бы лучше сразу по всем критериям. Экономический смысл понятия эффективное решение в следующем. Эффективное решение относительно какого-либо производства (в масштабах отдельной фирмы или всего народного хозяйства) означает, что увеличение выпуска одного продукта возможно лишь при уменьшении выпуска хотя бы одного другого продукта или при увеличении затрат ресурсов.

Множество эффективных векторов называют множеством

Парето, а любой вектор этого множества - оптимумом по Парето.

Для того чтобы лучше разобраться в понятии «эффективное решение», посмотрим, что такое неэффективное решение (вариант, альтернатива). Решение А неэффективное, если есть решение В такое, что В лучше А сразу по всем критериям. Надо иметь в виду, что решение может быть либо эффективным, либо неэффективным.

В качестве примера рассмотрим простую ситуацию. Человек собирается поместить свои свободные деньги в какой-либо (один) банк. Каждый вариант он оценивает по двум критериям: F₁– ставка процента по вкладу,F₂- вероятность возврата вклада с процентами как мера надежности банка. Результаты его анализа представлены на рис. 2. Варианты А и В - неэффективные, так как вариант С лучше, чем А и В сразу по двум критериям. Вариант С - также неэффективный, так как вариант Е лучше С сразу по двум критериям. Эффективными являются вариантыDи Е. Если человек захочет сделать выбор между этими вариантами, то ему надо либо бросить жребий, либо принять во внимание какие-либо дополнительные соображения (удобство местоположения банка, например). Если человек захочет распределить свои деньги между двумя банками, то получится задача, резко отличающаяся от задачи выбора одного банка.

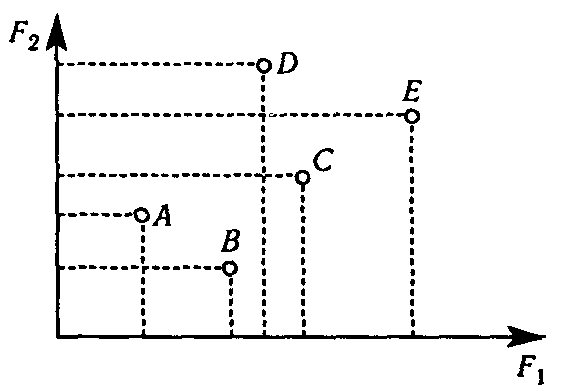
Рис. 2. Оценивание вариантов решений по двум критериям

Пусть теперь все множество допустимых вариантов ограничено осями F₁,F₂и пунктирно-сплошной кривой КАСВDР (рис. 3). Вариант Е - явно неэффективный, так как вариант С лучше по всем критериям. Для выделения множества эффективных решений надо провести такие линии уровней АК и ВК, которые дают максимальное значение критериев отдельно по каждому из них. Участок АВ (сплошная линия) - множество эффективных решений. В самом деле, решение А лучше, чем В поF₂, но хуже поF₁; С лучше А поF₁, но хуже поF₂и т. д. ТочкаD- неэффективная, так как для неё значения по обоим критериям хуже, чем для В. Видим, что эффективные решения лежат на границе допустимой области, но не каждая точка на этой границе - эффективное решение.

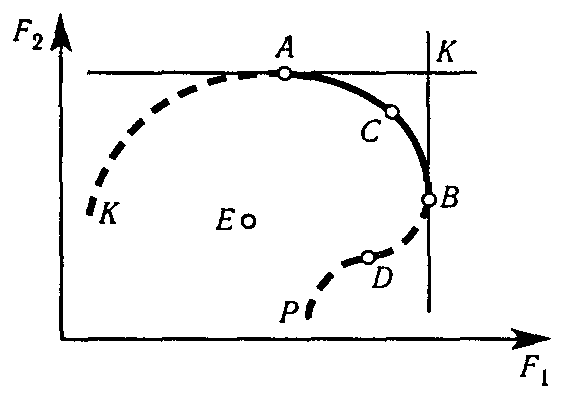
Рис. 3. Выделение эффективных решений

Как видно из рис. 4, множество эффективных решений может состоять из нескольких несвязанных подмножеств, например АВ и СD. Эти подмножества действительно содержат эффективные решения, так как К лучше Р поF₂, но хуже поF₁. Хороший менеджер, конечно, должен иметь в виду такой возможный вариант.

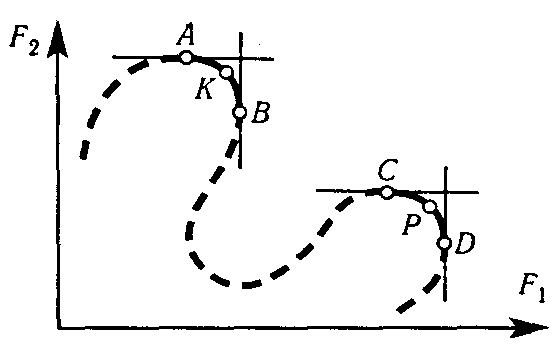
Рис. 4. Вариант множества эффективных решений

Наконец, рассмотрим ситуацию на рис. 5. Пусть когда-то допустимая область ограничивалась кривой МАРQBL. В этом случае эффективным был участок АВ, и вы пользовались вариантомQ. Потом ситуация изменилась, допустимой стала область МАРQBLCRKDZ. ВариантQперестал быть эффективным, так как вариант С (и не только он!) стал лучше сразу по всем критериям. Вариант К, который хуже дажеQпоF₂, тем не менее - эффективный, так как он лучше всех вариантов из АВ поF₁. Таким образом, изменение ситуации привело к сужению прежнего эффективного множества и появлению нового эффективного множества.

Рис. 5. Изменение множества эффективных решений

Варианты заданий

В пространстве критериев нарисовать точки, соответствующие отдельным вариантам решений. Найти точки, составляющие множество Парето.

Вариант 1. Критерий F₁– эффективность вариантов решений, критерийF₂– экономия времени при решении проблемы.

Вариант 2. Критерий F₁– прибыль от реализации вариантов решений, критерийF₂– время решения проблемы.

Вариант 3. Критерий F₁– затраты на реализацию вариантов решений, критерийF₂– время решения проблемы.

Вариант 4. Критерий F₁– время решения проблемы, критерийF₂– экономия средств при реализации вариантов решений.

Вариант 5. Критерий F₁– экономия времени при решении проблемы, критерийF₂– затраты на реализацию вариантов решений.

Из таблицы случайных чисел, полученных у преподавателя, выбрать по 10 значений для каждого критерия.

Например, студент гр. МП – 3, 35-й по списку, выбирает следующие исходные данные:

Решения	1	2	3	4	5	6	7	8	9	10
F1	35	02	40	08	64	94	45	87	42	74
F2	54	15	84	42	43	75	05	19	30	29

РЕШЕНИЕ ЗАДАЧ МНОГОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ МЕТОДОМ ПОСЛЕДОВАТЕЛЬНЫХ УСТУПОК

В практической деятельности часто встречаются задачи, заключающиеся в поиске лучшего (оптимального) решения при наличии различных несводимых друг к другу критериев оптимальности. Например, принятие решения о строительстве дороги в объезд города должно учитывать такие факторы, как выигрыш города в целом по соображениям экологии, проигрыш отдельных предприятий и фирм, например, из-за уменьшения проезжающих через город потенциальных покупателей и многие другие. Если такого рода задачи решаются методами математического программирования, то говорят о задачах многокритериальной оптимизации. Эти задачи могут носить как линейный, так и нелинейный характер. Поскольку методы решения таких задач излагаются ниже на примере линейных многокритериальных оптимизационных задач, это объясняет рассмотрение этой темы в данной главе учебного пособия.

Задачи многокритериальной оптимизации возникают в тех случаях, когда имеется несколько целей, которые не могут быть отражены одним критерием (например, стоимость и надежность). Требуется найти точку области допустимых решений, которая минимизирует или максимизирует все такие критерии. Если в подобного рода задачах речь идет не о разнородных критериях некоторой системы, а о сопоставлении однородных критериев разных ее подсистем (например, отрасли, группы населения и т.п.), то эти задачи называются задачами векторной оптимизации.

Обозначим i-й частный критерий черезZ_i(X), гдеХ - допустимое решение, а область допустимых решений - черезQ. Если учесть, что изменением знака функции всегда можно свести задачу минимизации к задаче максимизации, то кратко задачу многокритериальной оптимизации можно сформулировать следующим образом:

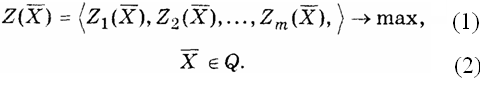
Некоторые частные критерии могут противоречить друг другу, другие действуют в одном направлении, третьи - индифферентны, безразличны друг к другу. Поэтому процесс решения многокритериальных задач неизбежно связан с экспертными оценками как самих критериев, так и взаимоотношений между ними. Известен ряд методов решения задач многокритериальной оптимизации:

• оптимизация одного признанного наиболее важным критерия, остальные критерии при этом играют роль дополнительных ограничений;

• упорядочение заданного множества критериев и последовательная оптимизация по каждому из них (этот подход рассмотрен ниже на примере метода последовательных уступок);

• сведение многих критериев к одному введением экспертных весовых коэффициентов для каждого из критериев таким образом, что более важный критерий получает более высокий вес.

Возвращаясь к задаче многокритериальной оптимизации в общей постановке (1), (2), отметим, что в идеальном случае можно вести поиск такого решения, которое принадлежит пересечению множеств оптимальных решений всех однокритериальных задач. Однако такое пересечение обычно оказывается пустым множеством, поэтому приходится рассматривать так называемое «переговорное множество эффективных решений (оптимальных по Парето). Критерий оптимальности итальянского экономиста В.Парето применяется при решении таких задач, когда оптимизация означает улучшение одних показателей при условии, чтобы другие не ухудшались.

Определение. Вектор называется эффективным (оптимальным по Парето) решением задачи (1), (2), если не существует такого вектора, что

причём хотя бы для одного значения iимеет место строгое неравенство.

Множество допустимых решений, для которых невозможно одновременно улучшить все частные показатели эффективности (т.е. улучшить хотя бы один из них, не ухудшая остальных), принято называть областью Парето, или областью компромиссов, а принадлежащие ей решения эффективными, или оптимальными по Парето.

В общем случае эффективные решения не эквивалентны друг другу, так что про два оптимальных по Парето решения нельзя сказать, какое из них лучше. Поэтому при решении многокритериальных задач необходимо дополнительное изучение эффективных решений. Для этого можно было бы сформулировать некоторый критерий и оптимизировать его на множестве эффективных решений. Однако при этом возникают значительные трудности в связи с тем, что, как правило, область компромиссов не является выпуклой, и полученная задача в общем случае будет задачей невыпуклого программирования. Обычный подход заключается в стремлении «свернуть частные критерии в один обобщенный скалярный критерий, оптимизация которого приводит к оптимальному решению задачи в целом. Формулировка подходящего обобщённого критерия в зависимости от конкретных условий как раз и является основным вопросом, который изучается в многокритериальной оптимизации.

В некоторых случаях вместо одного обобщённого критерия и решения одной соответствующей задачи скалярной оптимизации предлагается рассматривать последовательность обобщённых критериев и последовательность задач скалярной оптимизации. К сожалению, многие из описанных в литературе подобных процедур не всегда приводят к эффективным решениям.

Рассмотрим один из таких методов решения многокритериальных задач: метод последовательных уступок.

Метод последовательных уступок решения задач многокритериальной оптимизации применяется в случае, когда частные критерии могут быть упорядочены в порядке убывания их важности. Предположим, что все частные критерии максимизируются и пронумерованы в порядке убывания их важности. Находим максимальное значение Z₁^*первого по важности критерия в области допустимых решений путем решения однокритериальной задачи

Затем, исходя из практических соображений и принятой точности, назначается величина допустимого отклонения δ₁ > 0(экономически оправданной уступки) критерияZ₁ и находится максимальное значение второго критерия при условии, что значение первого критерия не должно отклоняться от своего максимального значения более чем на величину допустимой уступки, т. е. решается задача:

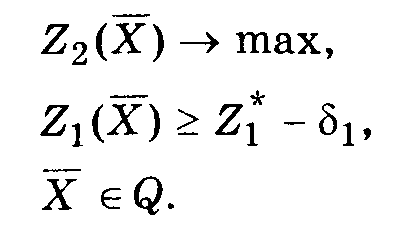
Снова назначается величина уступки δ₂ > 0 по второму критерию, которая вместе с первой уступкой используется для нахождения условного максимума третьего частного критерия:

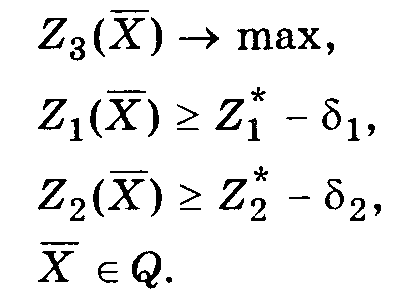
Аналогичные процедуры повторяются до тех пор, пока не будет выявлено максимальное значение последнего по важности критерия Z_mпри условии, что значение каждого из первыхm – 1частных критериев отличается от соответствующего условного максимума не более чем на величину допустимой уступки по данному критерию. Полученное на последнем этапе решение считается оптимальным. Следует заметить, что этот метод не всегда приводит к эффективному решению.

Пример 6. Решение задачи многокритериальной оптимизации методом последовательных уступок.

Пусть задача трехкритериальной оптимизации имеет вид:

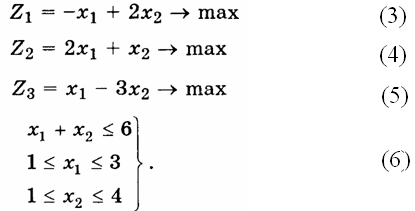
Для определенности будем считать, что допустимые уступки по первым двум критериям заданы: δ₁= 3; δ₂= 5/3.

Максимизируем функцию Z₁в области допустимых решений, т. е. решаем однокритериальную задачу (3), (6). Это несложно сделать графическим методом решения задач линейного программирования (рис. 6).

Рис. 6

Максимум функции Z₁при условиях (6) достигается в точкеАобластиQс координатами (1;4), так что в данном случае

Переходим к максимизации функции Z₂при условиях (6) и дополнительном ограничении, позволяющем учесть, что по критериюZ₁нельзя уступать более чем наδ₁. Так как в нашем примереZ₁^*-δ₁= 4, то дополнительное ограничение будет иметь вид:

Задачу (4), (6), (7) также решаем графически (рис. 7).

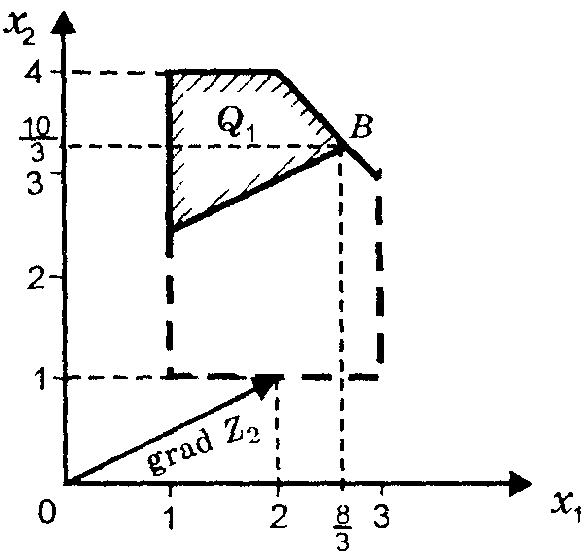
Рис. 7

Получаем, что максимум функции Z₂при условиях (6), (7) достигается в точкеВчастиQ₁областиQ, так что

Теперь уступаем по критерию Z₂ на величину уступки

δ₂= 5/3и получаем второе дополнительное ограничение:

Максимизируем функцию при условиях (6), (7) и (8). Решение этой задачи графическим методом представлено на рис. 8.

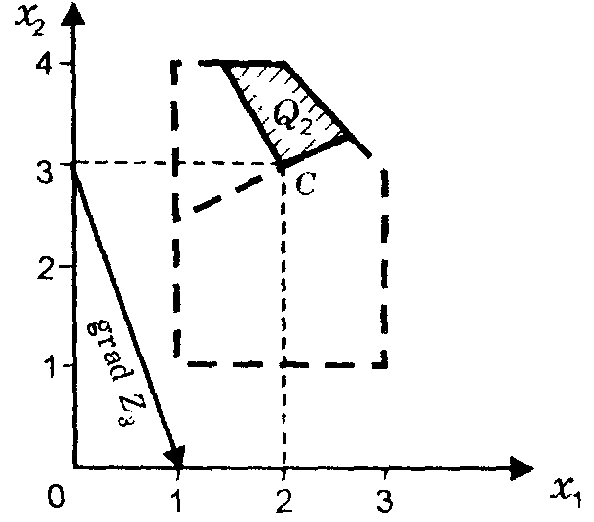
Рис. 8

Таким образом, получаем оптимальное решение рассматриваемой трехкритериальной задачи (точка С на рис. 8):

Соответствующие значения частных критериев при этом составляют:

Варианты заданий

Найти компромиссное решение, учитывая, что оптимальное решение должно удовлетворять величине, составляющей не менее 65% от значения, достигнутого по первому критерию.

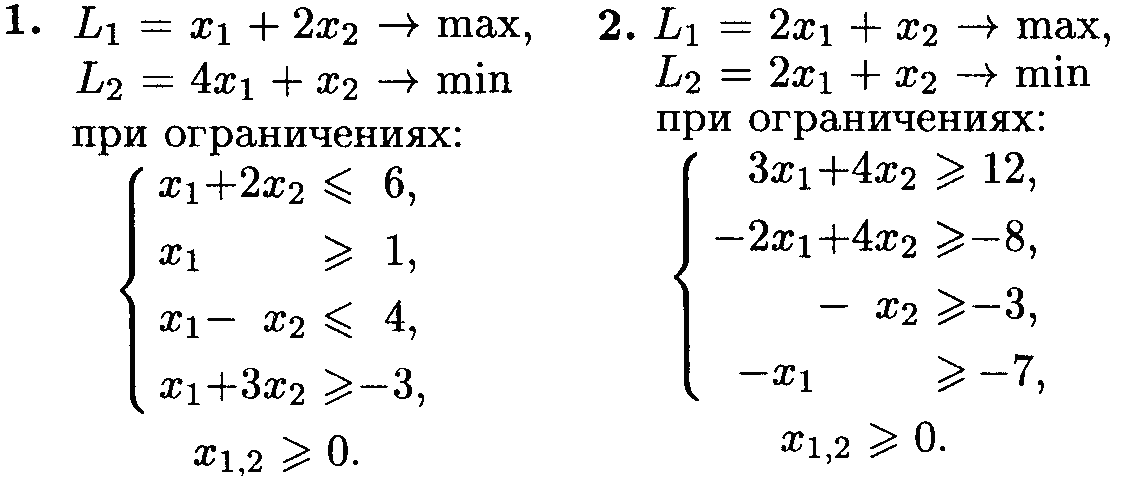
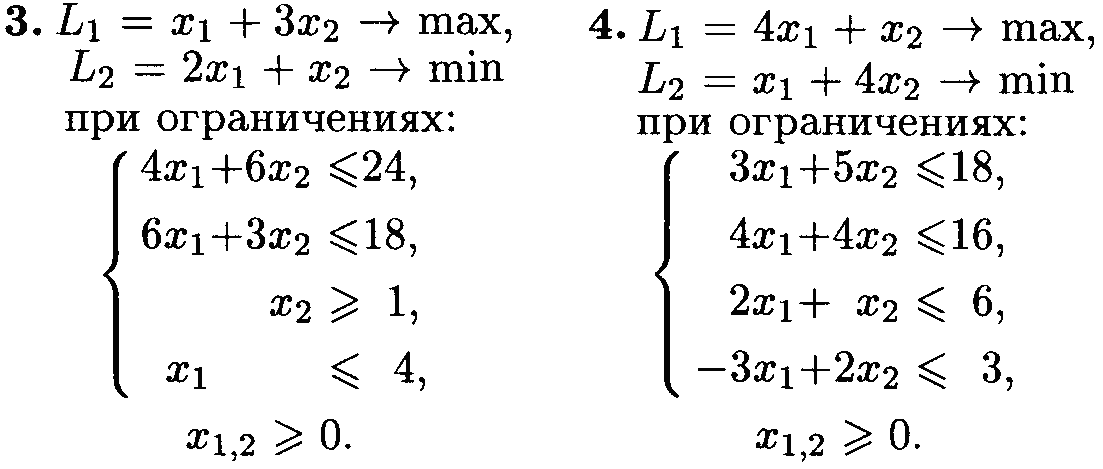
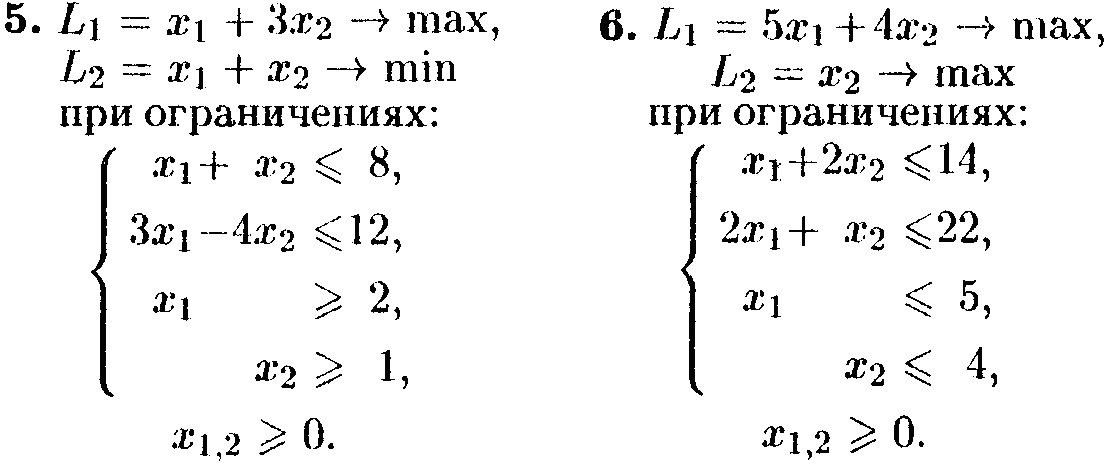
МЕТОД АНАЛИЗА ИЕРАРХИЙ

При принятии решений часто воздействие той или иной альтернативы не может быть выражено количественно, или же количественная оценка такого влияния представляется в виде широкого диапазона значений показателей, что не снимает фактора неопределенности решения. Кроме того, имеется ряд факторов, оцениваемых не абсолютными, а ранговыми (порядковыми) показателями.

Определение целей с помощью многих показателей дает возможность принимать решения на базе нескольких критериев, т.е. с ориентацией на множество целей.

Чтобы повысить рациональность принятия решений и расширить возможности человека в области обработки информации, необходимо провести декомпозицию сложной проблемы на более простые частные задачи. На это и ориентирован метод анализа иерархий (аналитико-иерархический процесс). Метод базируется на обработке порядковой, т.е. “мягкой” информации, поступающей в распоряжение лица, принимающего решения (ЛПР), и на основе этой неполной информации позволяет определить ряд альтернативных вариантов решения.

Система целей для принятия решений не всегда имеет конкретную форму, кроме того, сначала необходимо разработать целевые показатели, требующиеся для принятия решения. В ходе последовательного выявления и формулирования главных целей через определение целей более низкого порядка (подцелей) создается иерархическая целевая система. При этом требуется также установить различия в важности целей одного иерархического уровня. Однако с ростом числа критериев, учитываемых при оценке альтернативных вариантов решений, уменьшаются способности ЛПР в области анализа проблем.

Метод анализа иерархий (МАИ) может быть использован в принятии решений следующим образом: после того как фактор неопределенности решаемой проблемы оценен в форме различных сценариев развития внешней среды, проводится сопоставление пар этих сценариев с помощью порядковой шкалы для установления вероятности осуществления того или иного сценария. Такая шкала представлена в табл. 1.

Таблица 1

Шкала попарного сравнения альтернатив

Значения шкалы Vij	Вероятность одного сценария по сравнению с другим; сравнение важности двух подцелей; реализуемость цели с помощью стратегии i по сравнению со стратегией j
1	одинаково вероятны, важны, значимы
3 (1/3)	несколько вероятнее (невероятнее), важнее (неважнее), лучше (хуже)
5 (1/5)	ощутимо вероятнее (невероятнее), важнее (неважнее), лучше (хуже)
7 (1/7)	намного вероятнее (невероятнее), важнее (неважнее), лучше (хуже)
9 (1/9)	крайне вероятнее (невероятнее), важнее (неважнее), лучше (хуже)
2 (1/2), 4 (1/4), 6 (1/6), 8 (1/8)	промежуточные значения

Данная таблица используется для построения иерархии целей путем ответа на вопрос: какая из каждых двух сравниваемых подцелей важнее для достижения цели более высокого уровня. В результате возникает горизонтальный ряд. Путем порядковой оценки определяется, какая из каждых двух сравниваемых альтернатив предпочтительнее для наилучшего достижения поставленной цели. Полученные данные попарного сравнения сценариев, целей и альтернатив решений оформляются в виде матриц.

При сопоставлении двух объектов анализа выбирается соответствующее значение шкалы V_ij, сравнение этих же объектов в обратном порядке должно оцениваться обратной величиной V_ji = 1 / V_ij . Например, если менеджеры оценивают цель (Ц₁) “лидерство фирмы в области качества” как “несколько важнее” по сравнению с целью (Ц₂) “лидерство фирмы в области издержек”, то сопоставление в обратном порядке дает оценку “несколько неважнее”. Соответствующие значения по шкале будут V₁₂=3 и V₂₁=1/3.

Поскольку диапазон оценок шкалы ограничен, то оценочные суждения могут оказаться инконсистентными. Если, например, менеджмент поставит перед собой наряду с уже названными целями еще и цель (Ц₃) “защита окружающей среды” и при этом для менеджмента лидерство в издержках “намного важнее” (V_ij=7) по сравнению с добавленной целью, то консистентной оценкой для сопоставления важности целей “лидерство в издержках” и “защита окружающей среды”, следовало бы взять показатель V_ij, равный 21. Однако он не согласуется с предложенной шкалой, где максимальной является величина 9.

На базе парного ранжирования сценариев развития внешней среды и сравнительных суждений о каждой паре целей и стратегий с помощью МАИ можно количественно рассчитать вероятность этих сценариев, веса целей и приоритеты альтернативных вариантов решений.

Для расчета необходимо полностью заполнить матрицу попарных сравнений, учитывая, что V_ij=1/V_ji . Для каждой строки матрицы рассчитывается среднее геометрическое значение g_i и значимость (вероятность) альтернативы p_i как отношение соответствующей средней геометрической к сумме всех среднегеометрических оценок G.

Для каждого столбца матрицы определяется сумма оценок s_j .

Таблица 2

Матрица оценок попарного сравнения альтернатив

	1	2		j		n		pi=gi/G
1	V11	V12	…	V1j	…	V1n	g1	p1
2	V21	V22	…	V2j	…	V2n	g2	p2
	…	…	…	…	…	…	…	…
i	Vi1	Vi2	…	Vij	…	Vin	gi	pi
	…	…	…	…	…	…	…	…
n	Vn1	Vn2	…	Vnj	…	Vnn	gn	pn
	s1	s2	…	si	…	sn

Сумма произведений полученных суммарных оценок s_j и соответствующих значений вероятностей (приоритетов) позволяет определить максимальное собственное значение матрицы, которое должно быть не меньше, чем размерность матрицы λ_max ≥ n :

Коэффициент согласованности или инконсистентности (КИ) определяется следующим образом:

МАИ позволяет сблизить инконсистентные данные с консистентными. Если коэффициент инконсистентности превышает критическое значение КИ>0,1 , то менеджеры должны пересмотреть свои основные оценки.

Для проверки согласованности мнений экспертов определяется отношение согласованности ОС, как частное от деления коэффициента инконсистентности на величину случайной согласованности Сс, получаемую из специальных таблиц (табл. 3):

Считается приемлемым, если ОС ≤ 10%, допустимым, если ОС ≤ 20%, но если ОС > 20%, то оценки V_ij необходимо пересмотреть.

Таблица 3

Значения величины случайной согласованности

Размерность матрицы (n)	1	2	3	4	5	6	7	8	9	10
Случайная согласован-ность (Сс)	0	0	0,58	0,9	1,12	1,24	1,32	1,41	1,45	1,49

Построить графическую структуру иерархии целей и альтернатив. Оценить в качестве эксперта значимость целей и альтернатив с помощью метода анализа иерархий. Проранжировать альтернативы согласно расчета их значимости и выбрать наиболее предпочтительную альтернативу.

Вариант 1.

Цель – получение выгоды от реконструкции предприятий.

Критерии – прибыль, занятость, конкурентоспособность.

Альтернативы – тракторный завод, завод буровой техники, молочный завод.

Вариант 2.

Цель – получение выгоды от развития спортивно-оздоровительного комплекса.

Критерии – привлечение инвестиций, занятость подростков, здоровье населения.

Альтернативы – хоккейное поле, бассейн, теннисный корт.

Вариант 3.

Цель – получение выгоды от создания научного центра.

Критерии – новые технологии, образование, международные контакты.

Альтернативы – центр доступа к Интернету, институт разработки новых информационных технологий, центр социально-экономического прогнозирования развития региона.

Вариант 4.

Цель – получение выгоды от развития транспортного обслуживания.

Критерии – быстрая прибыль, рабочие места, экология.

Альтернативы – метро, троллейбусы, маршрутные такси.

Вариант 5.

Цель – создание эффективного предприятия в регионе.

Критерии – возможность получения земельного участка, наличие квалифицированного персонала, близость материальных ресурсов.

Альтернативы – нефтеперерабатывающее предприятие, автомобилестроительный завод, лесоперерабатывающая фабрика.

Задание № 2

ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ

НЕОПРЕДЕЛЕННОСТИ И РИСКА

“ДЕРЕВО РЕШЕНИЙ”

Принятие решения о замене оборудования в условиях неопределенности и риска.

Фирма может принять решение о замене старого оборудования на новое того же вида или его ремонте. Отремонтированное оборудование впоследствии можно частично заменить

на новое, более современное, или отремонтировать его заново.

Решение определяется будущим спросом на продукцию, которую производят на этом оборудовании.

Полная замена оборудования экономически оправданна при высоком уровне спроса. С другой стороны, можно отремонтировать старое оборудование и через один год, например, заменить его на новое, более совершенное, или заново его отремонтировать.

В данной задаче процесс принятия решения состоит из двух этапов: решение в настоящий момент времени о замене или ремонте оборудования и решение, принимаемое через один год, относительно частичной его замены и ремонта.

Пример 1. Задача о замене оборудования фирмы, представленная в виде дерева решений.

Предполагается, что спрос может оказаться высоким, средним и низким.

Дерево имеет два типа вершин: решающие и случайные.

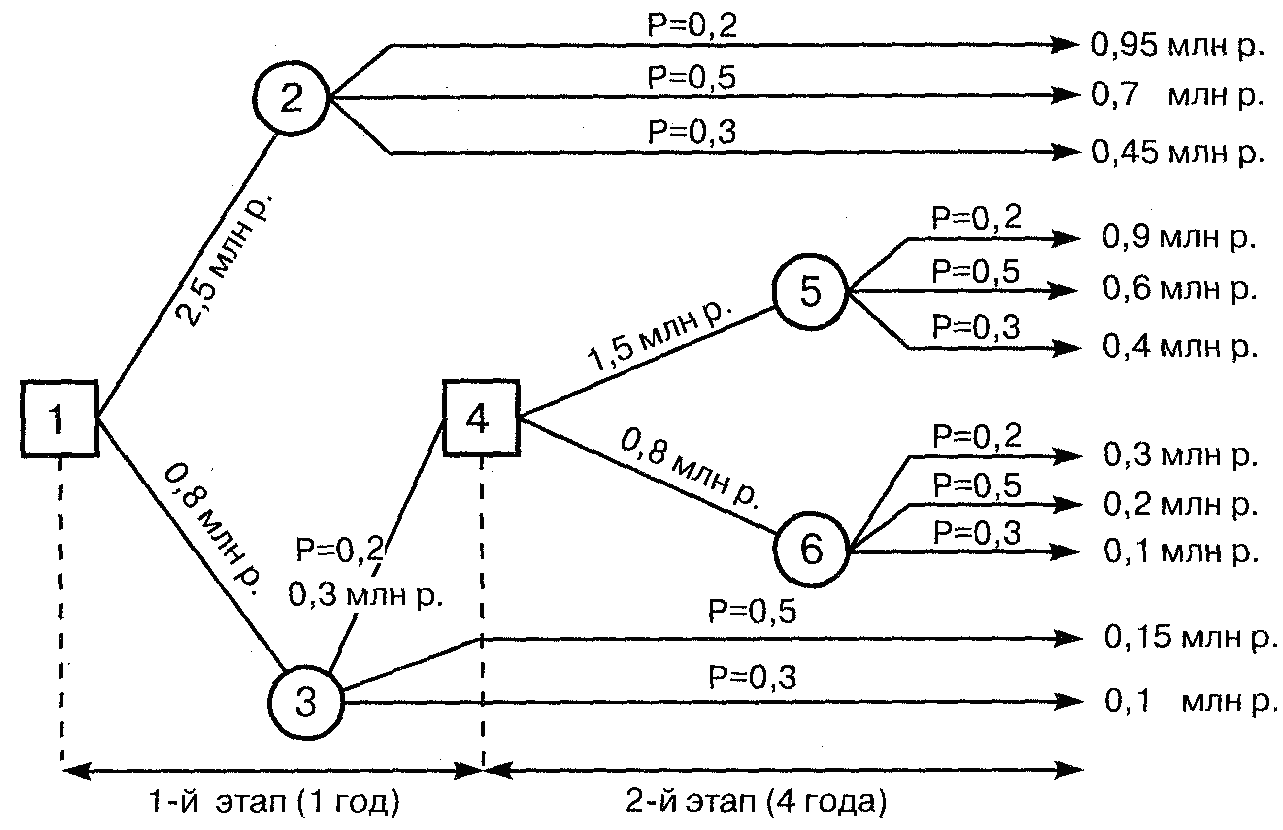
Начиная с решающей вершины 1 необходимо принять решение о полной замене оборудования или его ремонте.

Вершины 2 и 3 являются случайными. Фирма будет рассматривать возможность установления более совершенного оборудования или повторного ремонта старого в том случае, если спрос по истечении одного года установится на высоком уровне. Поэтому в вершине 4 принимается решение о частичной замене старого оборудования более совершенным или ремонте старого. Вершины 5 и 6 случайные.

Предположим, что фирма рассматривает эту задачу на пятилетний период. Анализ рыночной ситуации показывает, что вероятности высокого, среднего и низкого уровней спроса составляют 0,2, 0,5 и 0,3 соответственно. Замена новым оборудованием того же вида, что и старое, обойдется в 2,5 млн р., а ремонт старого - в 0,8 млн р.

Затраты на частичную замену оборудования на более совершенное, чем старое, оцениваются в 1,5 млн р., а повторный ремонт старого - в 0,8 млн р.

Ежегодные доходы для каждой стратегии фирмы следующие.

1. Замена старого оборудования на новое того же вида при высоком, среднем и низком уровнях спроса дает 0,95; 0,7 и 0,45 млн р. соответственно.

2. При ремонте старого оборудования при высоком, среднем и низком уровнях спроса доход оценивается в 0,3; 0,15 и 0,1 млн р. соответственно.

3. Частичная замена оборудования на более совершенное при высоком, среднем и низком уровнях спроса приносят 0,9;

0,6 и 0,4 млн р. соответственно.

4. Повторный ремонт старого оборудования при высоком, среднем и низком уровнях спроса предполагает доход в 03; 0,2 и 0,1 млн р. соответственно.

Определить оптимальную стратегию фирмы в замене оборудования.

РЕШЕНИЕ. Оценим результаты каждой стратегии и определим, какие решения следует принимать в решающих вершинах 1 и 4.

Вычисления начнем с этапа 2. для последних 4 лет альтернативы, относящиеся к вершине 4, оцениваются так:

ДЧЗ= (0,9•0,2 + 0,6•0,5 + 0,4•0,3) •4 - 1,5 = 0,9 млн р.,

ДДР = (0,3•0,7 + 0,2•0,5 + 0,1•0,3) •4 - 0,8 = -0,04 млн р.,

где ДЧЗ - доход от частичной замены оборудования на более совершенное, ДДР - доход от замены оборудования, прошедшего дважды ремонт. Так как ДЧЗ > ДДР, то в вершине 4 выгоднее произвести частичную замену оборудования на более совершенное, при этом доход составит 0,9 млн р.

Для дальнейших расчетов в вершине 4 можно оставить одну ветвь, которой соответствует доход в 0,9 млн р. за 4 года.

Вычислим доходы на 1-м этапе для решающей вершины 1:

ДЗН= (0,95•0,2 + 0,7•0,5 + 0,45•0,3) •5 - 2,5 = 0,875 млн р.,

ДЗО= 0,3•0,2•1+0,15•0,5•5+0,1•0,3•5+0,9 - 0,8 = 0,685 млн р.,

где ДЭН доход от замены старого оборудования на новое того же вида, ДЗО - доход от отремонтированного оборудования и дальнейшей замены на более совершенное.

Так как ДЭН > ДЗО, то оптимальным решением в вершине 1 является полная замена старого оборудования на новое того же вида.

Ответ. Оптимальной стратегией фирмы в замене оборудования является решение о полной замена старого оборудования на новое того же вида, при этом доход составит 0,875 млн р.

ОПРЕДЕЛЕНИЕ ПРОИЗВОДСТВЕННОЙ ПРОГРАММЫ ПРЕДПРИЯТИЯ В УСЛОВИЯХ РИСКА И НЕОПРЕДЕЛЕННОСТИ С ИСПОЛЬЗОВАНИЕМ МАТРИЧНЫХ ИГР

Фирма “Фармацевт” - производитель медикаментов и био- медицинских изделий в регионе. Известно, что пик спроса на некоторые лекарственные препараты приходится на летний период (препараты сердечно-сосудистой группы, анальгетики), на другие - на осенний и весенний периоды (антиинфекционные, противокашлевые).

Затраты на 1 усл. ед. продукции за сентябрь-октябрь составили: по первой группе (препараты сердечно-сосудистые анальгетики) - 20 р.; по второй группе (антиинфекционные, противокашлевые препараты) - 15 р.

По данным наблюдений за несколько последних лет службой маркетинга фирмы установлено, что она может реализовать в течение рассматриваемых двух месяцев в условиях теплой погоды 3050 усл. ед. продукции первой и 1100 усл. ед. продукции второй группы; в условиях холодной погоды - 1525 усл. ед. продукции первой группы и 3690 усл. ед. второй группы.

В связи с возможными изменениями погоды ставится задача - определить стратегию фирмы в выпуске продукции, обеспечивающую максимальный доход от реализации при цене продажи 40 р. за 1 усл. ед. продукции первой группы и 30 р. - второй группы.

РЕШЕНИЕ. Фирма располагает двумя стратегиями:

А₁- в этом году будет теплая погода;

А₂- погода будет холодная.

Если фирма примет стратегию А₁и в действительности будет теплая погода (стратегия природы В₁), то выпущенная продукция (3050 усл. ед. препаратов первой группы и 1100 усл ед. второй группы) будет полностью реализована и доход составит

3050•(40 - 20) + 1100•(30 - 15) = 77500 р.

В условиях прохладной погоды (стратегия природы В2) препараты второй группы будут проданы полностью, а первой группы только в количестве 1525 усл. ед. и часть препаратов останется нереализованной. доход составит

1525•(40 - 20) + 1100•(30 - 15) - 20•(3050 - 1525) = 16500 р.

Аналогично, если фирма примет стратегию А₂и в действительности будет холодная погода, то доход составит

1525•(40 - 20) + 3690•(30 - 15) = 85850 р.

При теплой погоде доход составит

1525•(40 - 20) + 1100•(30 - 15) - (3690 - 1100)•15 = 8150 р.

Рассматривая фирму и погоду в качестве двух игроков, получим платежную матрицу

В1 В2

А1 77500 16500

А2 8150 85850

Для решения задачи используются следующие выражения:

p₁ = (а₂₂ – а₂₁)/(а₁₁ – а₁₂+а₂₂ – а₂₁)

р₂ = (а₁₁ – а₁₂)/(а₁₁ – а₁₂ + а₂₂ – а₂₁) = 1 – p₁

V = (а₁₁•а₂₂ – а₂₁•а₁₂)/(а₁₁ – а₁₂ + а₂₂ – а₂₁).

p₁= (85850 – 8150)/(77500 – 16500 + 85850 – 8150) = 0,56

р₂= (77500 – 16500)/(77500 – 16500 + 85850 – 8150) = 0,44

V = (77500 85850 – 8150 16500) /(77500 – 16500 +

+ 85850 – 8150) = 47000

Ответ: следует выпускать

3050•0,56+1525•0,44 = 2379 усл.ед продукции 1 группы

1100•0,56+3690•0,44 = 2239,6 усл.ед. продукции 2 группы

Гарантированный доход составит 47000 руб

ПРИНЯТИЕ РЕШЕНИЙ В ИГРАХ С "ПРИРОДОЙ"

В матричных играх предполагается, что в них принимают участие два игрока, интересы которых противоположны. Поэтому действия каждого игрока направлены на увеличение выигрыша (уменьшение проигрыша). Однако в некоторых задачах, приводящихся к игровым, имеется неопределенность, вызванная отсутствием информации об условиях, в которых осуществляется действие (погода, покупательский спрос и т.д.). Эти условия зависят не от сознательных действий другого игрока, а от объективной действительности.

Такие игры называются играми с природой. Человек в играх с природой старается действовать осмотрительно, второй игрок (природа, покупательский спрос) действует случайно.

Условия игры задаются матрицей

(a_{i j}) _{m x n}

Имеется ряд критериев, которые используются при выборе оптимальной стратегии. Рассмотрим некоторые из них.

1. Критерий Байеса. Решение о выборе i-й стратегии принимается с учетом вероятностей состояний природы

mах_i Σ_j{а_ij • q_j}

q_j – вероятностьj-го состояния природы.

2. Критерий Лапласа. Выбирается стратегия, имеющая максимальное значение среднего выигрыша

mах_i {1/n • Σ_j а_ij}

где 1/n • Σ_j а_ij – средний выигрыш по каждой строке, соответствующейi-й стратегии,n– количество состояний природы.

3. Критерий Вальда. Рекомендуется применять максиминную стратегию. Она достигается из условия

mах_i {min_j а_ij}

и совпадает с нижней ценой игры (из минимальных выигрышей по каждой строке выбирается максимальный). Критерий является пессимистическим, считается, что природа будет действовать наихудшим для человека образом.

4. Критерий Сэвиджа. Суть критерия состоит в выборе такой стратегии, чтобы не допустить чрезмерно высоких потерь, к которым она может привести. Находится матрица рисков, элементы которой показывают, какой убыток понесет человек (фирма), если для каждого состояния природы он не выберет наилучшей стратегии.

Элемент матрицы рисков (r _{i j}) находится по формуле

{mах_i a_ij} - a_ij

где mах_i a_ij- максимальныйi-й элемент в каждом столбце исходной матрицы.

Оптимальная стратегия находится из выражения

min_i {max_j r_ij}

5. Критерий Гурвица. Критерий рекомендует стратегию, определяемую по формуле

max_i {k min_j a_ij + (1 - k) max_j a_ij},

где k- степень оптимизма изменяется в диапазоне [0, 1].

Критерий придерживается некоторой промежуточной позиции, учитывающей возможность как наихудшего, так и наилучшего поведения природы. При k= 1 критерий превращается в критерий Вальда, приk= 0 - в критерий максимакса. На а оказывает влияние степень ответственности лица, принимающего решение по выбору стратегии. Чем хуже последствия ошибочных решений, больше желания застраховаться, тем а ближе к единице.

6. Критерий максимакса. Он выбирается из условия

max_i {max_j a_ij} .

Критерий является оптимистическим, считается, что природа будет наиболее благоприятна для человека.

Пример: Выбор рациональной стратегии при неопределенной рыночной конъюнктуре с помощью методов теории статистических игр

Предприятие "Пиковая дама" должно определить уровень выпуска продукции и предоставления услуг на некоторый период времени, так, чтобы удовлетворить потребности клиентов. Точная величина спроса на продукцию и услуги неизвестна, но ожидается, что в зависимости от соотношения сил на рынке товаров, действий конкурентов и погодных условий, спрос может принять одно из четырех возможных значений: 300, 400, 500 или 600 изделий. Маркетинговые исследования позволили определить возможные вероятности возникновения этих ситуаций, которые соответственно составили 0,2; 0,4; 0,3 и 0,1. Для каждого из возможных значений спроса существует наилучший уровень предложения, с точки зрения возможных затрат и прибыли, отклонение от этих уровней связано с риском и может привести к дополнительным затратам либо из-за превышения предложения над спросом, либо из-за неполного удовлетворения спроса. В первом случае это связано с необходимостью хранения нереализованной продукции и потерями при реализации ее по сниженным ценам, во втором – с дополнительными затратами по оперативному выпуску недостающей продукции, т.к. иначе это будет связано с риском потери клиентов. Данную ситуацию можно представить в виде матрицы игры (табл.4).

Таблица 4

Анализ стратегий производства при неопределенной

рыночной конъюнктуре

Объем предложения	Возможные колебания спроса на продукцию
	П1 = 300	П2 = 400	П3 = 500	П4 = 600
	Вероятность состояния спроса
	q1 = 0,2	q2 = 0,4	q3 = 0,3	q4 = 0,1
	Размер прибыли (убытков) в зависимости от колебаний спроса (аij)
С1 = 300	30	22	16	8
С2 = 400	6	40	32	24
С3 = 500	-18	16	50	42
С4 = 600	-42	-8	36	60

Для выбора наилучшей стратегии поведения на рынке товаров и услуг существуют различные критерии, среди которых можно назвать критерии: Байеса, Лапласа, Вальда, Сэвиджа, Гурвица и максимакса. Считается, что вернее будет выбрать ту стратегию, которая будет предпочтительнее по нескольким критериям.

По критерию Байеса наилучшая стратегия определяется выражением:

где a_ij - размер "выигрыша" при выборе i-й стратегии при j-м состоянии "природы"; q_j - вероятность возникновения j-го состояния "природы".

В₁ = 30 ٠ 0,2 + 22 ٠ 0,4 + 16 ٠ 0,3 + 8 ٠ 0,1 = 20,4

В₂ = 6 ٠ 0,2 + 40 ٠ 0,4 + 32 ٠ 0,3 + 24 ٠ 0,1 = 29,2

В₃ = -18 ٠ 0,2 + 16 ٠ 0,4 + 50 ٠ 0,3 + 42 ٠ 0,1 = 22,0

В₄ = -42 ٠ 0,2 - 8 ٠ 0,4 + 36 ٠ 0,3 + 60 ٠ 0,1 = 4,8

Наилучшая стратегия В₂ дает максимальный средний "выигрыш" в размере 29,2.

По критерию Лапласа:

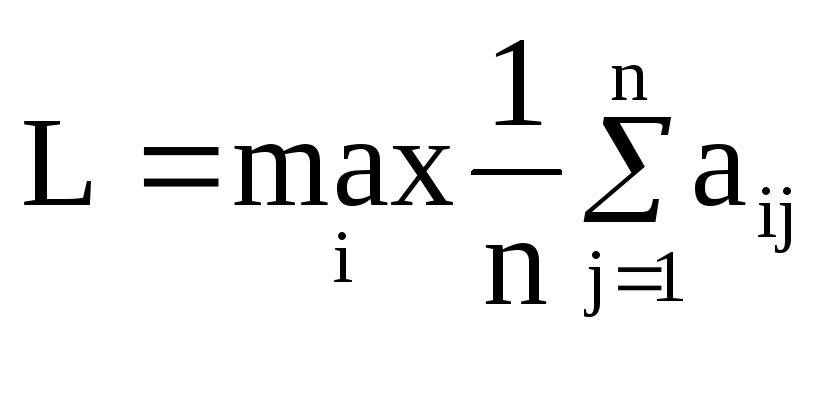
L₁ = (30 + 22 + 16 + 8) / 4 = 19

L₂ = ( 6 + 40 + 32 + 24) / 4 = 25,5

L₃ = (-18 + 16 + 50 + 42)/ 4 = 22,5

L₄ = (-42 - 8 + 36 + 60)/ 4 = 11,5

Наилучшая стратегия L₂ дает максимальный средний "выигрыш" в размере 25,5.

По критерию Вальда:

W₁ = 8; W₂ = 6; W₃ = -18; W₄ = -42.

Наилучшая стратегия W₁ дает максимальный "выигрыш" в размере 8.

По критерию Сэвиджа наилучшая стратегия соответствует минимальному риску:

где r_ij - размер риска при выборе i-й стратегии при j-м состоянии "природы";

r_ij =

r₁₁ = 30 - 30 = 0; r₁₂ = 40 - 22 = 18; r₂₁ = 30 - 6 = 24 и т.д., в результате получаем матрицу рисков.

Матрица рисков

Стратегии	Состояния «природы»
	П1 = 300	П2 = 400	П3 = 500	П4 = 600
С1 = 300	0	18	34	52	52
С2 = 400	24	0	18	36	36
С3 = 500	48	24	0	18	48
С4 = 600	72	48	14	0	72

Наилучшая стратегия S₂ дает минимальный риск.

По критерию Гурвица:

где k - коэффициент "пессимизма", примем k = 0,3.

G₁ = 0,3 ٠ 8 + 0,7 ٠ 30 = 23,4

G₂ = 0,3 ٠ 6 + 0,7 ٠ 40 = 29,8

G₃ = 0,3 ٠ (-18) + 0,7 ٠ 50 = 29,6

G₄ = 0,3 ٠ (-42) + 0,7 ٠ 60 = 29,4.

Наилучшая стратегия G₂ дает "выигрыш" 29,8.

По критерию максимакса:

Наивыгоднейшая стратегия может дать "выигрыш" в размере 60, но ей же соответствует и наибольший риск (72).

По большинству критериев наилучшая стратегия

С₂ = 400 изделий.

"ДЕРЕВО РЕШЕНИЙ"

Решить задачу с использованием “дерева” решений. Фирма планирует построить среднее или малое предприятие по производству пользующейся спросом продукции. Решение о строительстве определяется будущим спросом на продукцию, которую предполагается выпускать на планируемом предприятии.

Строительство среднего предприятия экономически оправданно при высоком спросе, но можно построить малое предприятие и через 2 года его расширить.

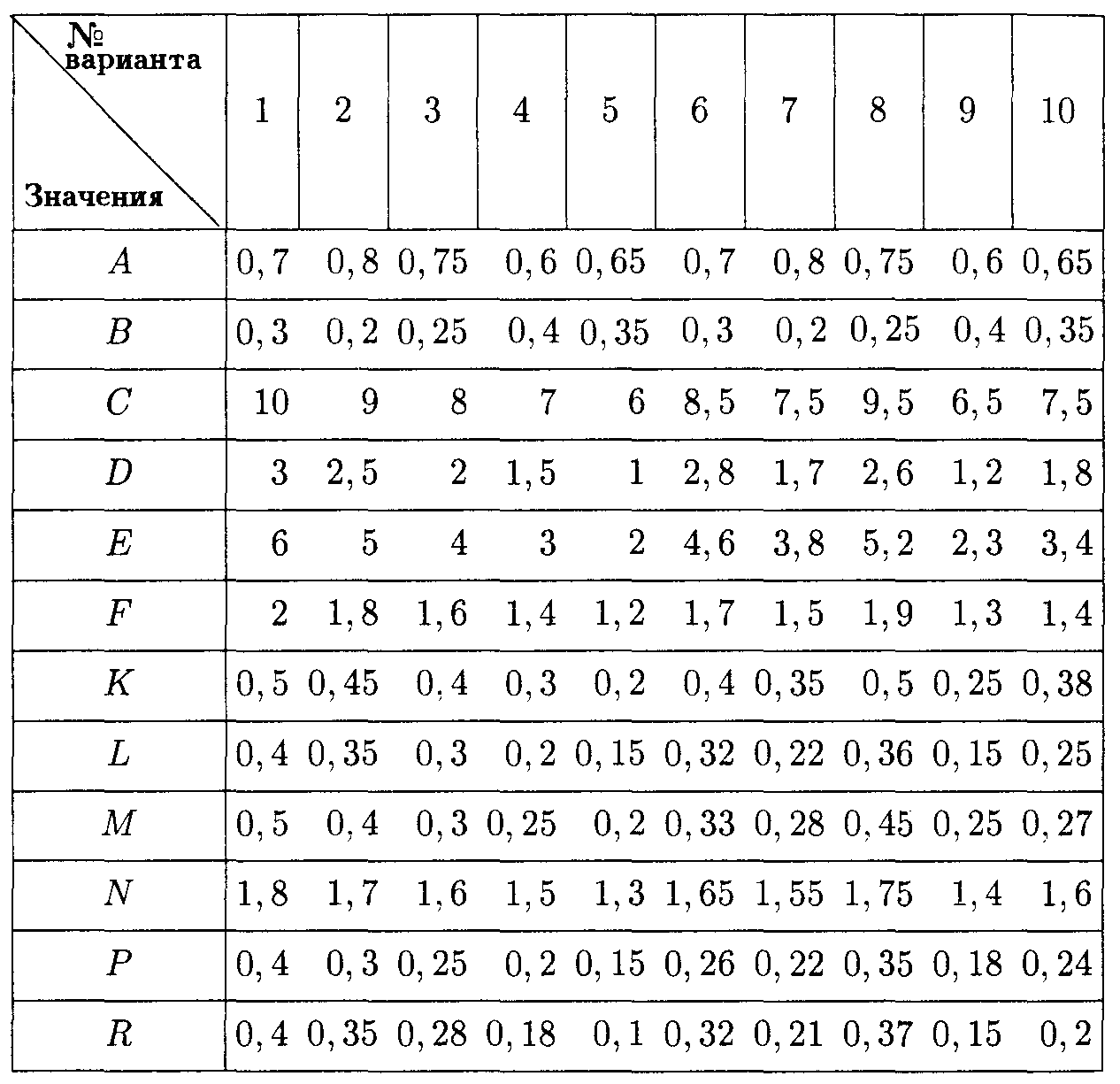
Фирма рассматривает данную задачу на десятилетний период. Анализ рыночной ситуации, проведенный службой маркетинга, показывает, что вероятности высокого и низкого уровней спроса составляют А и В соответственно.

Строительство среднего предприятия составит С млн р.,

малого - Dмлн р. Затраты на расширение малого предприятия оцениваются в Е млн р.

Ожидаемые ежегодные доходы для каждой из возможных

альтернатив:

• среднее предприятие при высоком низком спросе – F, а при низком - К млн р.;

• малое предприятие при низком спросе - Lмлн р., а при высоком спросе - М млн р.;

• расширенное предприятие при высоком спросе дает N, а при низком - Р млн р.;

• малое предприятие без расширения при высоком спросе в течение первых двух лет и последующем низком спросе дает Rмлн р. за остальные 8 лет.

Определить оптимальную стратегию фирмы в строительстве предприятий по выпуску продукции.

Значения коэффициентов условия задачи

НЕОПРЕДЕЛЕННОСТЬ В МАТРИЧНОЙ ИГРЕ

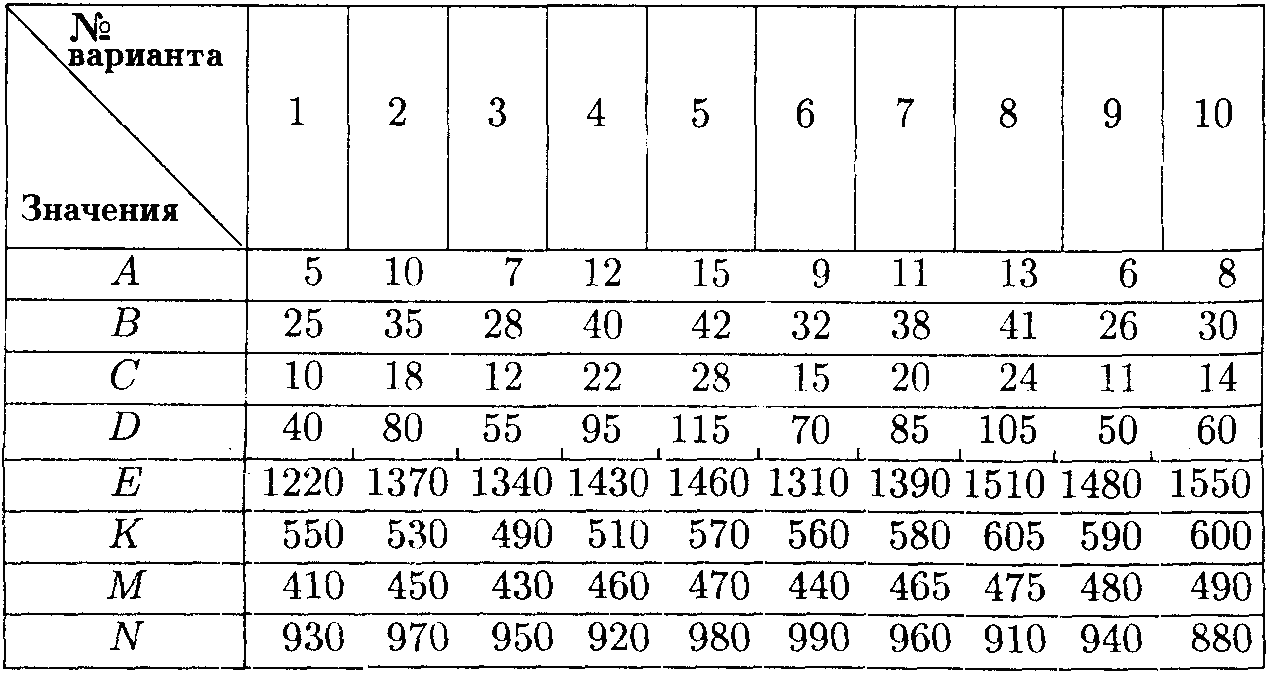
Фирма производит пользующиеся спросом платья и костюмы, реализация которых зависит от состояния погоды. Затраты фирмы в течение апреля-мая на единицу продукции составят: платья А ден. ед., костюмы В ден. ед. Цена реализации составит С ден. ед. и Dден. ед. соответственно.

По данным наблюдений за несколько предыдущих лет, фирма может реализовать в условиях теплой погоды Е шт. платьев и К шт. костюмов, при прохладной погоде М шт. платьев и Nшт. костюмов.

В связи с возможными изменениями погоды определить стратегию фирмы в выпуске продукции, обеспечивающую ей

максимальный доход. Задачу решить аналитическим методом.

Значения коэффициентов условия задачи

НЕОПРЕДЕЛЕННОСТЬ И РИСКИ В ИГРЕ С ПРИРОДОЙ

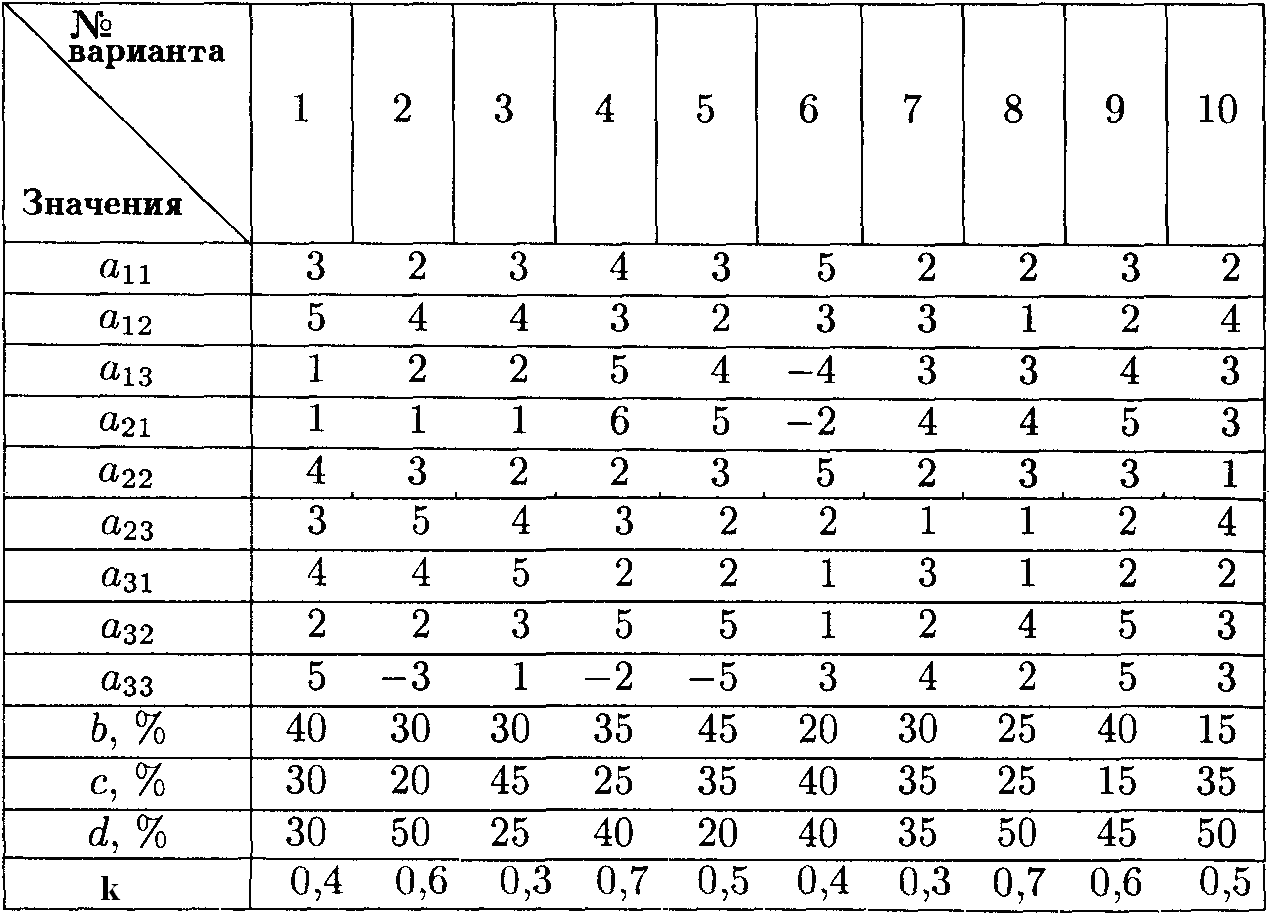
Торговая фирма разработала несколько вариантов плана продаж товаров на предстоящей ярмарке с учетом конъюнктуры рынка и спроса покупателей. Получающиеся от их возможных сочетаний показатели дохода представлены в таблице.

1) Определить оптимальную стратегию фирмы в продаже

товаров на ярмарке.

2) Если существует риск (вероятность реализации плана П₁-b%, П₂- с%, П₃-d%),то какую стратегию фирме следует считать оптимальной?

Задачу решить с использованием критериев игр с природой, приняв степень оптимизма k, указанную в таблице.

Значения параметров условия задачи

Выбор вариантов каждой части задания

производится преподавателем согласно

спискам студентов по группам

СОДЕРЖАНИЕ РАЗДЕЛОВ ДИСЦИПЛИНЫ