
- •Кафедра автоматизированных и вычислительных систем
- •3.1. Методы минимизации логических функций на основе прямых преобразований сднф
- •3.2. Метод испытания импликант
- •3.3. Визуальные методы минимизации логических функций
- •3.3.2. Метод минимизации полностью определенных логических функций с помощью карт Карно
- •3.3.3. Метод минимизации частично определенных логических функций с помощью карт Карно
- •Содержание
- •Минимизация логических функций и их реализация на плм
- •394026 Воронеж, Московский просп., 14
3.1. Методы минимизации логических функций на основе прямых преобразований сднф
Одним из первых таких строго формализованных методов является метод Квайна. Сущность этого метода состоит в следующем: если над исходной СДНФ произвести сначала все возможные операции неполного склеивания, а затем над полученным выражением все возможные операции поглощения, то в результате выполненных преобразований будет получена сокращенная ДНФ.
Проиллюстрируем
применение метода Квайна для минимизации
логической функции
![]() ,
заданной следующей таблицей истинности
(табл. 3.1.):
,
заданной следующей таблицей истинности
(табл. 3.1.):
Таблица 3.1
|
a |
b |
c |
|
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
Выпишем
СДНФ функции
![]() :
:
![]() (3.1)
(3.1)
Пронумеруем каждую конъюнкцию из (3.1) следующим образом:
![]() (3.2)
(3.2)
Затем, склеиваем (если это возможно) каждый из членов выражения (3.2) с последующими членами и записываем полученные импликанты так, как показано в таблице 3.2:
Таблица 3.2
|
Номера склеиваемых конъюнкций |
Импликанты, полученные в результате склеивания (если склеивание возможно) |
|
1-2 |
|
|
1-3 |
|
|
1-4 |
не склеиваются |
|
1-5 |
не склеиваются |
|
1-6 |
не склеиваются |
|
2-3 |
не склеиваются |
|
2-4 |
|
|
2-5 |
не склеиваются |
|
2-6 |
не склеиваются |
|
3-4 |
не склеиваются |
|
3-5 |
|
|
3-6 |
не склеиваются |
|
4-5 |
не склеиваются |
|
4-6 |
|
|
5-6 |
|
Соединяя
полученные импликанты знаками дизъюнкции,
получаем сокращенную ДНФ логической
функции
![]() :
:
![]() (3.3)
(3.3)
Используя метод Квайна для минимизации логических функций необходимо помнить о том, что в этом методе используется операция неполного склеивания. Если в СДНФ, реализующей логическую функцию, присутствует конъюнкция, которая не может быть склеена ни с одной последующей конъюнкцией, то эта конъюнкция должна быть включена в полученную в результате минимизации сокращенную ДНФ.
3.2. Метод испытания импликант
После получения сокращенной ДНФ, к ней может быть многократно применен метод Квайна, в результате чего будет получена некоторая тупиковая форма тождественная исходной ДНФ. Более часто применяют другой метод: метод испытания импликант в сокращенной ДНФ логической функции.
Существо метода состоит в следующем: из формулы, являющейся сокращенной ДНФ, выбирается испытуемая импликанта (можно произвольным образом). Выбранная импликанта приравнивается к 1. Далее определяются значения логических переменных, обращающих в 1 испытуемую импликанту. Из сокращенной ДНФ удаляется испытуемая импликанта, а в оставшуюся часть сокращенной ДНФ подставляются найденные значения логических переменных, обращающих в 1 испытуемую импликанту. Если в результате такой подстановки значение логической функции равно единичному значению, то испытуемая импликанта является лишней (избыточной) и может быть удалена из сокращенной ДНФ логической функции. После удаления лишней импликанты также испытываются все импликанты, входящие в сокращенную ДНФ.
Рассмотрим метод испытания импликант на примере.
Пусть
логическая функция
![]() ,
представлена в виде сокращенной ДНФ,
полученной по методу Квайна (3.3):
,
представлена в виде сокращенной ДНФ,
полученной по методу Квайна (3.3):
![]() (3.3)
(3.3)
Испытаем
импликанты в (3.3). Первой будем испытывать
импликанту
![]() .
.
Импликанта
![]() обращается в 1 при следующих значениях
логических переменных:
обращается в 1 при следующих значениях
логических переменных:
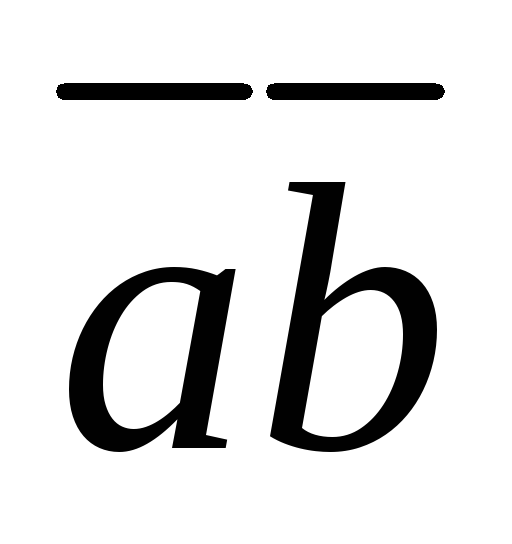 =1,
при
=1,
при
 =0,
=0,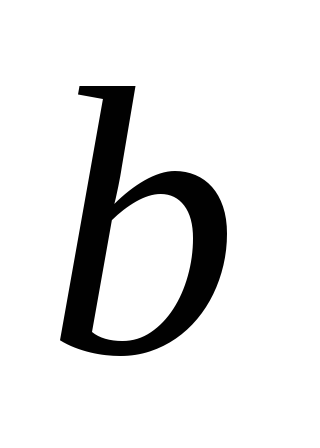 =0.
Подставляя найденные значения в (3.3),
предварительно исключив из формулы
испытуемую импликанту, получим:
=0.
Подставляя найденные значения в (3.3),
предварительно исключив из формулы
испытуемую импликанту, получим:
![]() импликанта
импликанта
![]() является лишней и должна быть удалена
из формулы.
является лишней и должна быть удалена
из формулы.
Таким же образом испытаем оставшиеся в формуле импликанты.
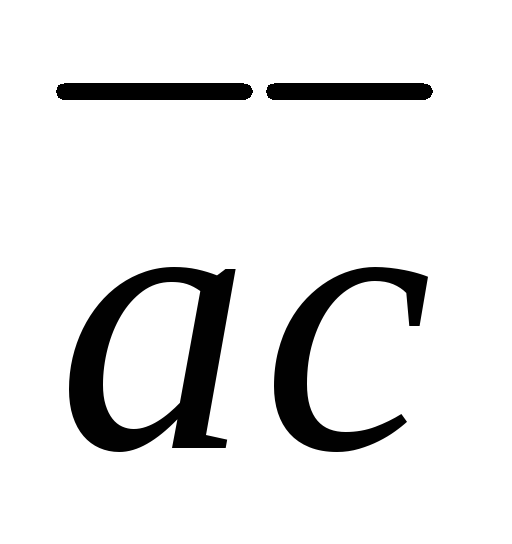 =1,
при
=1,
при
 =0,
=0, =0.
=0.
![]() импликанта
импликанта
![]() не является лишней. Оставляем ее в
формуле.
не является лишней. Оставляем ее в
формуле.
 при
при
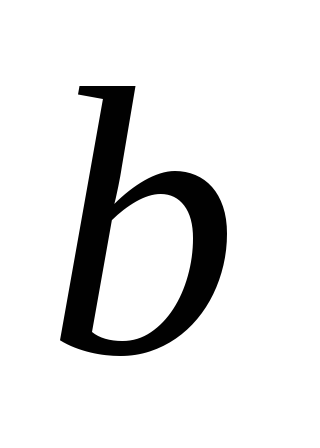 =0,
=0, =1.
=1.
![]() импликанта
импликанта
![]() не является лишней. Оставляем ее в
формуле.
не является лишней. Оставляем ее в
формуле.
 =1,
при
=1,
при
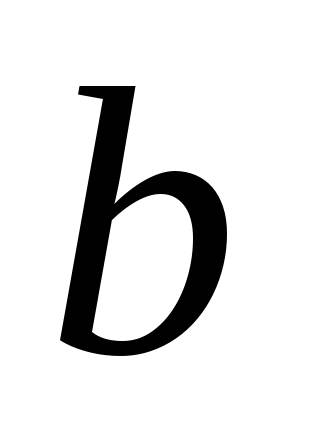 =1,
=1, =0.
=0.
![]() импликанта
импликанта
![]() является лишней и должна быть удалена
из формулы.
является лишней и должна быть удалена
из формулы.
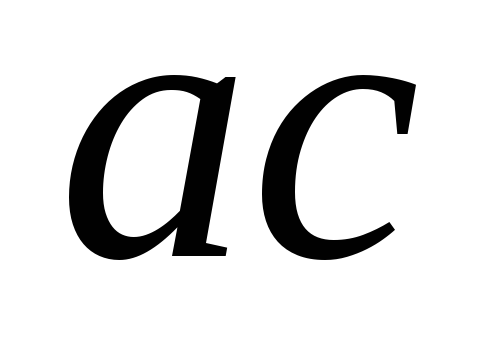 =1,
при
=1,
при
 =1,
=1, =1.
=1.
![]() импликанта
импликанта
![]() является лишней и должна быть удалена
из формулы.
является лишней и должна быть удалена
из формулы.
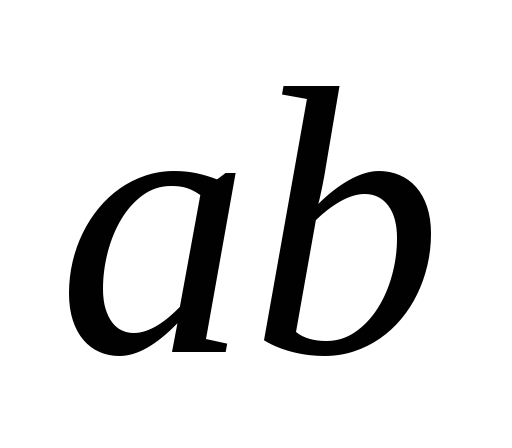 =1,
при
=1,
при
 =1,
=1,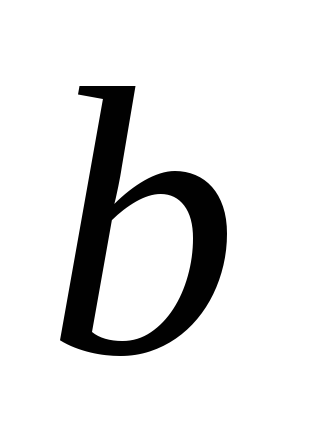 =1.
=1.
![]() импликанта
импликанта
![]() не является лишней. Оставляем ее в
формуле.
не является лишней. Оставляем ее в
формуле.
После
испытания импликант получаем одну из
тупиковых ДНФ логической функции
![]() :
:
![]() (3.4)
(3.4)
Если
начать испытание импликант в (3.3) не с
первой импликанты, а с какой-либо другой,
выбранной произвольным образом, то
можно получить некоторое количество
тождественных сокращенных и тупиковых
ДНФ, реализующих функцию![]() .
В частности, если начать испытание
импликант с последней импликанты в
(3.3), то полученная тупиковая ДНФ для
логической функции
.
В частности, если начать испытание
импликант с последней импликанты в
(3.3), то полученная тупиковая ДНФ для
логической функции![]() будет иметь вид:
будет иметь вид:
![]() (3.5)
(3.5)
