2. Эксперименты с устройствами, имеющими два входа и один выход

Представим дискретное устройство с двумя входами и одним выходом в виде «черного ящика» (рис. 1.4).

Рассмотрим исследуемую установку, исходные условия те же: черный ящик имеет кнопку К и лампочку L, только в данном случае лампочка должна загораться в определенный момент времени, задаваемый значением переменной С.

Рис. 1.4. Черный ящик с двумя входами и одним выходом

Условимся, что если С=1, то момент времени, когда лампочка должна загореться настал, а если С=0 лампочка по времени не должна гореть. Из проведенного опыта мы обнаружили, что элементы в исследуемой системе имеют по два состояния (кнопка нажата – не нажата, лампочка горит – не горит, момент времени настал - не настал).

Цифра 1 обозначает воздействие (кнопка нажата, момент времени загорания лампочки настал) или результат (лампочка горит). Цифра 0 обозначает отсутствие воздействия (кнопка не нажата, момент времени загорания лампочки не настал) или отсутствие результата (лампочка не горит). Тогда таблица результатов эксперимента будет иметь вид (табл.1.5):

Таблица 1.5.

К	С	L
0	0	0
0	1	0
1	0	0
1	1	1

Из таблицы 1.5 видно, что дискретное устройство дает на выходе логическую 1 (L = 1 – лампочка горит) только в одном единственном случае: на входе К = 1 и на входе С = 1, т.е. должны выполняться два условия, кнопка должна быть нажата и сигнал загорания лампочки тоже должен поступить.

Из таблицы 1.5 видно также, что количество всех возможных экспериментов над таким автоматом уже достаточно значительно, а именно 16. Для общности дальнейших рассуждений каждую входную переменную будем обозначать как , а выходную – как F .

Эксперименты проводятся с каждым дискретным устройством по очереди, а результаты этих экспериментов записываются в таблицу. Тогда результаты всех возможных экспериментов можно свести в сводную таблицу 1.6.

Таблица 1.6.

Сводная таблица результатов экспериментов исследования дискретного устройства с двумя входами и одним выходом.

x1	x2	F 0	F 1	F 2	F 3	F 4	F 5	F6	F 7	F 8	F 9	F 10	F 11	F 12	F 13	F 14	F 15
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

В таблице 1.7 представлены те же самые 16 логических функций, их наименование и математическое выражение языком алгебры логики.

Таблица 1.7.

Сводная таблица логических функций двух аргументов.

Аргументы и функции	Значения аргументов				Наименование функций	Запись функций
						Специальные обознач- ния	В ДНФ или КНФ
	0	0	1	1
	0	1	0	1
F0	0	0	0	0	Константа 0
					Продолжение таблицы 1.7.
F1	0	0	0	1	Конъюнкция, логическое умножение И	*, &, И
F2	0	0	1	0	Запрет по	←
F3	0	0	1	1	Повторитель
F4	0	1	0	0	Запрет по	←
F5	0	1	0	1	Повторитель
F6	0	1	1	0	Исключающее ИЛИ; сумма по модулю два	=1
F7	0	1	1	1	Дизъюнкция, лог. сложение, ИЛИ
F8	1	0	0	0	Стрелка Пирса, ИЛИ - НЕ
					Продолжение таблицы 1.7.
F9	1	0	0	1	Эквиваленция или равнозначность
F10	1	0	1	0	Инверсия
F11	1	0	1	1	Импликация от к
F12	1	1	0	0	Инверсия
F13	1	1	0	1	Импликация от к
F14	1	1	1	0	Штрих Шеффера, И - НЕ
F15	1	1	1	1	Константа 1	F15 = 1	F15 = 1

Задание N1.

Придумать схемы дискретных устройств, поведение которых можно описать одной из шестнадцати логических функций из таблицы 1.6. и дать им характеристику (словами и с помощью таблицы результатов экспериментов).

Контрольные вопросы:

1.1. Сущность метода «черного ящика».

1.2. Как построить таблицу экспериментов?

1.3. Что такое комбинационный автомат?

1.4. Когда можно создать более или менее удачную гипотезу о внутреннем устройстве «черного ящика»?

Лабораторная работа N2

Цель работы: изучение основных терминов и понятий, наиболее широко используемых в алгебре логики, получение практических навыков в их использовании.

2. МАТЕМАТИЧЕСКИЕ ОСНОВЫ АЛГЕБРЫ ЛОГИКИ.

2.1. Формальное определение алгебры логики

Алгебра логики является теоретической основой проектирования современных цифровых автоматов и базируется на символической логике, предложенной математиком Джорджем Булем. Существует множество формальных определений булевых алгебр [1,2], зависящих от различных подходов к выбранной системе аксиом.

Булева алгебра может быть определена как алгебраическая система, удовлетворяющая следующим аксиомам [3].

Булевой алгеброй является система, состоящая из множества

и двух типов операторов + и * (логическая сумма и логическое произведение), для которых справедливы следующие пять соотношений:

(коммутативность); (2.1)

(дистрибутивность); (2.2)

найдутся, такие, что

для любого (единичные элементы); (2.3)

найдется, такой, чтодля

любого (дополнение); (2.4)

(2.5)

с учетом того, что 1 > 0.

О

дним из вариантов булевой алгебры может служить алгебраическая система, в которой множествоB содержит всего два элемента , и которые одновременно являются единичными элементами. При этом, соотношение (2.4) можно трактовать как введение дополнительной (третьей) логической операцией, которую называют "отрицание" или "инверсия". Именно такую, самую простую, алгебраическую систему булевой алгебры и принято называть в научно-технической литературе алгеброй логики, переключательной алгеброй, алгеброй релейно - контактных схем.

2.2. Аксиомы, теоремы и законы алгебры логики

Алгебра логики в качестве аргументов использует логические переменные. Логические переменные и функции от них могут быть либо истинными (равными 1), либо ложными (равными 0). Логические переменные принято обозначать строчными латинскими буквами, а логические функции - прописными латинскими буквами.

В алгебре логики определены отношение эквивалентности (=) и три логические операции [4]: дизъюнкция (называют также логическое сложение, операция ИЛИ); конъюнкция (называют также логическое умножение, операция И); отрицание (называют также инверсия, операция НЕ).

По аналогии с обычной алгеброй операцию ИЛИ обозначают в виде + или (знак дизъюнкции); операцию И обозначают *, или, или & (знак конъюнкции); операцию НЕ обозначают чертой над переменными или над значениями переменных, например,. Знак *, как и в обычной алгебре, чаще всего опускают (например,

x * y = xy).

Отношение эквивалентности удовлетворяет следующим свойствам: x = x – рефлективность; если x = y, то y = x – симметричность; если x = y и y = z, то x = z – транзитивность. Из отношения эквивалентности следует принцип подстановки: если x = y, то в любой формуле, содержащей x, можно подставить y и будет получена эквивалентная формула.

2.3 Аксиомы алгебры логики

(2.6)

Аксиома (2.6) утверждает, что значения логических переменных и функций могут принимать всего два взаимоисключающих значения. Данную аксиому иногда называют " закон исключенного третьего". Следует помнить, что "1" и "0" - это не количественные характеристики, а качественные. Однако принимается, что 1 › 0.

(2.7)

Аксиома (2.7) определяет операцию дизъюнкции (логического сложения). Аксиома справедлива для любого числа слагаемых.

(2.8)

Аксиома (2.8) определяет операцию конъюнкции (логического умножения). Аксиома справедлива для любого числа сомножителей.

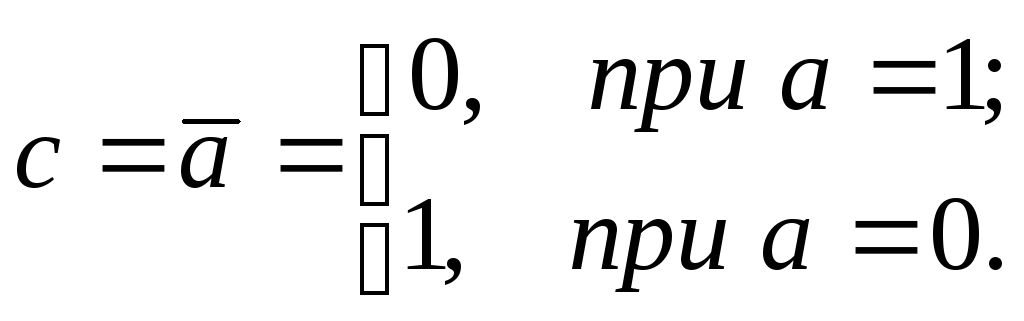(2.9)

Аксиома (2.9) определяет операцию логического отрицания (инверсию).

В алгебре логики действует закон двойственности, который определяет соотношение между логической операцией «или», логической операцией «и» и логической операцией «не». Суть этого закона такова: если в уравнениях все переменные поменять на инверсные (противоположные) значения и заменить знак «ИЛИ» на знак «И» и наоборот, то получим эквивалентные уравнения.

2.4 Теоремы алгебры логики.

Теоремы (2.10 - 2.19) легко доказываются с помощью аксиом (2.6- 2.9) и метода подстановки возможных значений аргументов x.

2.5. Законы алгебры логики.

Коммутативный закон (переместительный закон):

относительно логического сложения

x + y = y + x, (2.20 а)

относительно логического умножения

x * y = y * x . (2.20 б)

Данный закон гарантирует получение тождественного результата при перестановке местами аргументов.

Ассоциативный закон (сочетательный закон):

относительно логического сложения

x + y + z = y + (x + z) = (y + x) + z, (2.21 а)

относительно логического умножения

x * y * z = y * (x * z) = (y * x) * z. (2.21 б)

Данный закон позволяет при помощи скобок изменять порядок вычислений и гарантирует получение правильного результата, а также утверждает, что вычисление логической функции большого количества аргументов может быть сведено к последовательному ее вычислению суперпозицией функций двух аргументов.

Дистрибутивный закон (распределительный закон):

относительно логического сложения

x + (y * z) = (x + y) *( x + z), (2.22 а)

относительно логического умножения

x *(y + z) = (x * y) + ( x * z). (2.22 б)

Данный закон устанавливает правила раскрытия скобок относительно операций логического сложения и умножения.

Законы (правила) де Моргана:

(2.23 а)

(2.23 б)

Законы де Моргана определяют правила перехода от логической операции умножения к сложению (2.23 а) и наоборот (2.23 б).

Закон (2.23 а) утверждает, что отрицание конъюнкции, есть дизъюнкция отрицаний.

Закон (2.23 б) утверждает, что отрицание дизъюнкции, есть конъюнкция отрицаний.

Законы де Моргана называют также законами двойственности.

Как и в обычной алгебре в алгебре логики определен порядок выполнения логических операций: первой выполняется операция инверсии; второй - конъюнкции; третьей - дизъюнкции.

Задание N2.1.

Используя законы, аксиомы и теоремы алгебры логики упростить следующие выражения:

1. 6.

2. 7.

3. 8.

4. 9. ;

5.10.

Контрольные вопросы:

2.1.1. Сформулируйте законы алгебры логики.

2.1.2. Перечислите аксиомы алгебры логики.

2.1.3. Докажите теоремы алгебры логики с помощью аксиом.

2.1.4. В чем состоит суть закона двойственности?

2.5. Основные понятия и определения

Любая научно - техническая дисциплина использует специфическую терминологию, что позволяет лаконично и однозначно обмениваться информацией между специалистами соответствующего профиля.

Рассмотрим основные термины и понятия, наиболее широко пользуемые в алгебре логике.

Логическая (двоичная) переменная характеризует простое высказывание, которое содержит одну законченную мысль. Она обозначается буквой, например, х и может принимать значения 0 или 1.

Л

огическая функция — это сложное высказывание, состоящее из нескольких простых, связанных между со­бой соединительными союзами. Она записывается анали­тически в виде Y = f(x₁,x₂, ..., x_n), где х_i— двоичная пе­ременная, х_i { 0,1};Y{0,1 }.

Входной набор — это определенная комбинация зна­чений двоичных переменных в логической функции. Мак­симальное число входных наборов определяется выраже­нием m = 2ⁿ, где n — число переменных. Максимальное число логических функций n переменных определяется выражением N = 2 ^m = 2^2ⁿ.

Полностью определенная функция – это логическая функция, имеющая определенные значения 0 или 1 на всех входных наборах.

Частично определенная функция – это логическая функция, значения которой определены не на всех входных наборах. На тех входных наборах, где функция не определена, проставляется прочерк (или любой другой символ, отличный от 0 и 1).

Рабочие наборы – это входные наборы, для которых логическая функция полностью определена.

Безразличные наборы - это входные наборы, для которых логическая функция не определена. Частично определенную функцию, в конечном счете, делают полностью определенной (доопределяют), приписав безразличным наборам 0-е или 1-е значения функции. Простейший способ доопределения логической функции - произвольный (случайный) выбор значений, равных 0 или 1.

В алгебре логики существуют понятия: элементарная конъюнкция/дизъюнкция, конституента единицы/нуля, ранг элементарной конъюнкции/дизъюнкции, соседние элементарные конъюнкции/дизъюнкции.

Элементарные конъюнкция/дизъюнкция-это конъюнкция/дизъюнкция входных переменных, имеющих или не имеющих отрицаний. Любой символ переменной в элементарной конъюнкции/дизъюнкции может встречаться один раз.

Например, f₁ (x₁, x₂, x₃, x₄)= x₁x₂x₃x₄ есть элементарная конъюнкция, а ине являются элементарными конъюнкциями.

Ранг элементарной конъюнкции/дизъюнкции - число входных переменных в элементарной конъюнкции/дизъюнкции. Так, f₁ (x₁)= x₁- это элементарная конъюнкция первого ранга; f₂(x₁, х₂ , х₃)= x₁х₂x₃ — элементарная конъюнкция третьего ранга.

Конституента единицы (минтерм) - логическая функция от n аргументов, которая принимает значение, равное единице, только на одном наборе аргументов.На остальных наборах функция равна нулю.Минтерм можно также определить как элементарную конъюнкцию максимального ранга, на которой значение логической функции равно 1. Логическая сумма всех минтермов равна 1.

Конституента нуля (макстерм) - логическая функция от n аргументов, которая принимает значение, равное нулю, только на одном наборе аргументов.На остальных наборах функция равна единице.Макстерм можно также определить как элементарную дизъюнкцию максимального ранга, на которой значение логической функции равно 0. Логическое произведение всех макстермов равно 0.

Соседние элементарные конъюнкции /дизъюнкции — две элементарные конъюнкции /дизъюнкции одного и того же ранга, если они являются функциями одних и тех же переменных и отличаются только знаком отрицания (ин­версии) одной из переменных. Например, конъюнкции и являются соседними, так как они - функции одних и тех же переменных и отличаются зна­ком инверсии только одной переменной х₁.

На основе законов алгебры логики могут быть сфор­мулированы правила преобразования логических выра­жений .

Правило склеивания для соседних элементарных конъюнкций: логическую сумму двух соседних элемен­тарных конъюнкции некоторого ранга r можно заменить одной элементарной конъюнкцией ранга r-1, являю­щейся общей частью исходных слагаемых. Это правило является следствием распределительного закона. Например,

Правило склеивания для соседних элементарных дизъ­юнкций: логическое произведение двух соседних элементарных дизъюнкций ранга r можно заменять одной эле­ментарной дизъюнкцией ранга r - 1, являющейся общей частью исходных дизъюнкций. Это правило является следствием распределительного закона и применяется для упрощения логических выражений. На­пример:

Правило поглощения для элементарных конъюнкций: дизъюнкцию двух элементарных конъюнкций разных ран­гов, из которых одна является собственной частью другой, можно заменить конъюнкцией, имеющей меньший ранг. Это правило является следствием распределитель­ного закона. Например,

Кроме того, справедливы выражения:

Правило поглощения для элементарных дизъюнкций: логическое произведение двух элементарных дизъюнкций разных рангов, из которых одна является общей частью другой, можно заменить дизъюнкцией, имеющей меньший ранг. Это правило является следствием распределитель­ного закона и находит широкое применение для упрощения логических функций. Например,

Задание N2.2.

1. Воспользовавшись определениями элементарной конъюнкции/дизъюнкции и ее ранга, определить, являются ли следующие функции элементарной конъюнкцией/дизъюнкцией и, если являются, то найти их ранг:

1.6.

2. 7.

3. 8.

4. 9.

5. 10.

2. Являются ли соседними и элементарными следующие конъюнкции/дизъюнкции:

1. 6.

2. 7.

3. 8.

4. 9.

5. 10.

3. Используя правила поглощения и склеивания для соседних элементарных конъюнкций/дизъюнкций упростить следующие логические выражения:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

Контрольные вопросы:

2.2.1. Какая логическая функция называется полностью определенной, частично определенной?

2.2.2. Что такое входной набор и как определить максимальное число входных наборов?

2.2.3. Сформулируйте правила поглощения для элементарных дизъюнкций/конъюнкций.

2.2.4. Сформулируйте правила склеивания для соседних элементарных конъюнкций/дизъюнкций.

2.6. Формы представления логических функций.

2.6.1. Словесная форма представления логических функций

Любая логическая функция может быть представлена в виде словесного описания.

Пример 6.2. Функция f от двух переменных истинна тогда и только тогда, когда обе переменные одновременно ложны.

Пример 6.3. Функция g от трех переменных истинна только тогда, когда одновременно истинны не менее двух аргументов.

Функция g определена (задана) достаточно лаконично, но вместе с тем, не достаточно определенно. Для полной определенности данную функцию нужно было бы задать следующим образом: функция истинна тогда, когда одновременно истинны аргумент первый и второй, или когда истинны аргумент первый и третий, или когда истинны аргумент второй и третий, или когда истинны все три аргумента.

Таким образом, словесное описание логических функций усложняется по мере увеличения числа аргументов, что может приводить к неоднозначности задания функции. Однако и при небольшом числе аргументов словесное описание логической функции может выглядеть в форме, достаточно трудной для понимания. Рассмотрим в качестве примера следующую арабскую мудрость, которая выражает целесообразность общения между людьми.

Пример.

"Если не знает, и не знает, что он не знает,

тот глуп - избегай его.

Если не знает, и знает, что он не знает,

ученик - научи его.

Если знает, и не знает, что он знает,

тот спит - разбуди его.

Если знает, и знает, что он знает,

мудрец - учись у него".

Эта арабская мудрость может интерпретироваться как логическая функция двух аргументов (знает/не знает, знает/не знает), которая рекомендует не общаться только с глупцами.

Словесная форма задания логических функций наиболее часто используется на начальном этапе проектирования комбинационных автоматов.

2.6.2 Табличная форма представления логических функций.

Логическую функцию можно представить в табличной форме (таблицей истинности или картой Карно). Рассмотрим принцип построения таблиц истинности.

Таблица истинности — представление логической функции в виде таблицы. Таблица истинности содержит (n + k) столбцов и 2ⁿ строк, где n — число логических переменных, а k - число логических функций от n переменных.

В таблице истинности перечисляются (записываются) все возможные входные наборы логических переменных и указываются значения логических функций на каждом из входных наборов логических переменных. Для того, чтобы правильно перечислить все возможные входные наборы логических переменных, можно придерживаться следующего правила заполнения таблицы истинности: все логические переменные, определяющие логическую функцию, номеруются (начиная справа) целыми числами от 0 до n-1. Каждой логической переменной в таблице истинности, начиная сверху, присваивают чередующиеся группы значений (начиная с 0) через 2^j элементов в группе, где j - номер логической переменной (рис.2.1).

2n-1	2n-2	22	21	20
Xn-1	Xn-2	………….......		X0	Y
a	b	………………		q
		0	0	0
		0	0	1
		0	1	0
		0	1	1
		1	0	0
		1	0	1
		1	1	0
		1	1	1

Рис. 2.1. Пример заполнения таблицы истинности для одной логической функции n аргументов

Иными словами, для правильного заполнения таблицы истинности можно представить каждый входной набор значений логических переменных двоичным n-разрядным числом, и записать все возможные двоичные числа в порядке возрастания их значений, начиная со значения, равного нулю.

В правый крайний столбец (столбцы) таблицы истинности записываются значения логической функции.

В таблице 2 представлена в табличной форме логическая функция .

Таблица 2.1.

Таблица истинности функции f

х2	х1	f
0	0	1
0	1	0
1	0	0
1	1	0

Карта Карно - это прямоугольник, разбитый на единичны квадраты (клетки), число которых равно числу входных наборов логической функции, т.е. 2ⁿ. Каждая клетка карты соответствует одному входному набору. Клетки размечают так, чтобы наборы, которые соответствуют смежным минтермам (макстермам), располагались бы в соседних ячейках карты Карно. Координатами каждой клетки карты Карно являются комбинации переменных из всех возможных входных наборов логической функции.

Для двух переменных карта Карно представляет со­бой квадрат, разделенный на четыре клетки, по одной на каждый входной набор. Строки карты связаны с перемен­ной x₁, столбцы — с переменной х₂ .

Следовательно, рас­положенная слева вверху ячейка соответствует входному набору (0,0) или минтерму (), а расположенная спра­ва внизу ячейка — входному набору (1,1) или макстерму (x₁ v x₂).Такого рода карта называется картой Карно на две переменные (рис. 2.2). Представление логической функции на карте Карно производится в соответствии, с таблицей истинности. Если функция F(x_1, x₂) = x_1* x₂=1 на входном наборе (0,0), то это отражается на карте Карно записью в левую верхнюю ячейку единицы (рис. 2.2а). Остальные ячейки остаются незаполненны­ми. Карта Карно может заполняться нулями в те ячейки, на входных наборах которых функция равна нулю. На рис. 2.2,б приведен пример заполнения карты Карно для тех наборов, на которых функция f = 0,

		X2						X2
		0	1					0	1
X1	0	1				X1	0		0
	1						1	0	0
	f=1						f=0
	а)						б)

Рис.2.2. Изображение функции f на карте Карно

Карта Карно (табл.2 и рис.2.2), со­держит все 2ⁿ возможных входных наборов и значения функции, соответствующие каждому из наборов.

В

случае трех переменных карта Карно содержит восемь ячеек, по одной для каждого входного набора, указанного внутри ячейки. Переменнаяx₁свя­зана с двумя строками карты, а переменные x₂ и x₃ — с четырьмя столбцами. Таким образом, любые две рядом расположенные ячейки являются соседними и их коор­динаты отличаются только одной переменной. Кроме того, соседними являются ячейки, стоящие в первом и последнем столбцах карты.

Карта Карно обладает свойством цилиндричности: смежными являются минтермы или макстермы, расположенные в двух крайних столбцах, и расположенные в двух крайних строках.

Карты Карно наиболее эффективны не для первичного задания логических функций, а для упрощения (минимизации) аналитических выражений, задающих логические функции.

Задание N2.3.

1. Построить таблицу истинности для функции М(a,b,c), если известно, что:

а) функция истинна тогда, когда одновременно истинны не менее двух ее аргументов. В остальных случаях функция ложна;

б) функция истинна тогда, когда одновременно истинны не менее двух ее аргументов. В остальных случаях функция не определена;

в) функция ложна тогда, когда одновременно истинны не менее трех ее аргументов. В остальных случаях функция не определена;

г) функция истинна тогда, когда одновременно ложны не менее двух ее аргументов. В остальных случаях функция ложна;

д) функция ложна тогда, когда одновременно ложны не менее двух ее аргументов. В остальных случаях функция не определена.

2. Построить карту Карно для логических функций F_i (x₀, x₁, x₂), где i=0,…,9, заданной табл. 2.2, которая является таблицей истинности этих функций.

Таблица 2.2.

x2	x1	x0	F0	F1	F2	F3	F4	F5	F6	F7	F8	F9
0	0	0	1	1	0	0	1	1	0	1	1	1
0	0	1	0	1	1	0	1	1	1	1	0	0
0	1	0	0	0	0	0	0	1	1	1	1	1
0	1	1	1	1	1	1	0	0	1	1	1	1
1	0	0	0	0	0	0	1	1	0	0	0	0
1	0	1	1	0	1	0	1	0	1	0	1	0
1	1	0	0	1	0	1	0	1	0	1	1	0
1	1	1	1	0	1	0	1	1	1	0	1	1

3. Построить карту Карно для функции G(x₀, x₁, x₂, x₃, x₄, x₅), в ячейки карты вписать десятичный номер входного набора из таблицы истинности данной функции.

Контрольные вопросы:

2.3.1. Как заполняется таблица истинности?

2.3.2. Что такое карта Карно?

2.3.3. Какой вид табличного представления логической функции на ваш взгляд наиболее удобен, поясните.

2.6.3. Аналитическая форма представления логических функций.

Табличные способы задания логических функций становятся весьма громоздкими с увеличением числа аргументов. Так, уже при восьми аргументах количество строк в таблице истинности или количество клеток карты Карно равно 256. Аналитические формы представления логических функций более компактны и наглядны, и позволяют очень просто синтезировать комбинационные автоматы из ограниченного количества логических элементов, реализующих логические операции умножения (конъюнкцию), сложения (дизъюнкцию) и отрицания (инверсию). В то же время, аналитические формы логических функций позволяют выполнять различные их математические преобразования с целью получения более простых соотношений или для каких - либо других целей.

Аналитический способ предусматривает запись логической функции в форме логического выражения, показывающего, какие логические операции над аргументами должны выполняться и в какой последовательности. Сложные функции от многих аргументов могут быть представлены в форме "функций от функций", т.е. выражаться через более простые функции - от меньшего числа аргументов. Операция замены аргументов одной функции другими, более простыми функциями носит название суперпозиции функции. Многократное использование принципа суперпозиции дает возможность получить функции желаемого числа аргументов.

Для аналитического задания логических функций используются, так называемые, нормальные формы.

В алгебре логики существует две самые распространенные аналитические формы представления функции: совершенная дизъюнктивная нормальная форма (СДНФ) и совершенная конъюнктивная нормальная форма (СКНФ). Каждая логическая функция имеет одну СДНФ и одну СКНФ.

СДНФ логической функции может быть получена путем многократного применения теоремы разложения к некоторой функции n аргументов для каждой ее переменной x_i (i=1…n). Применяя теорему разложения, получим:

(2.24)

где f_i - значение логической функции на i -ом входном наборе аргументов;

m_i - i -ый минтерм или i -ая элементарная конъюнкция максимального ранга.

Из (2.24) следует, что СДНФ логической функции — это дизъюнкция конституент единицы (минтермов), соответствующих наборам входных переменных, для которых функция равна едини­це. Совершенная дизъюнктивная нормальная форма записывается для истинного значения логической функции. В то же время относительно логической функции можно сказать, что она истинна тогда, когда не ложна. Такое утверждение можно формализовать следующим образом.

Образуем логическую функцию по ее нулевым значениям на всех входных наборах. Тогда

(2.25)

Применяя к (2.25) правило де Моргана, получим

(2.26)

где f_i - значение логической функции на i -ом входном наборе аргументов;

M_i - i -ый макстерм или i -ая элементарная дизъюнкция максимального ранга.

Представление логической функции в виде (2.26) называется совершенной конъюнктивной нормальной формой (СКНФ).

СКНФ логической функции — это конъюнкция конституент нуля (макстермов), соответствующих входным наборам, для которых функция равна нулю.

Рассмотрим алгоритмы перехода от табличного описания логической функции к ее аналитическому описанию (СДНФ, СКНФ).

Алгоритм перехода от таблицы истинности логической функции к ее записи в виде СДНФ:

1) выбрать в таблице истинности такие входные наборы, на ко­торых функции обращается в единицу;

2) по каждому такому набору составить элементарные конъюнкции максимального ранга (минтермы);

3) в минтермы записать не инвертированными переменные, заданные единицей в таблице истинности, а инвертированными - те переменные, которые в таблице истинности заданы нулем;

4) полученные минтермы соединить между собой знаками дизъюнкции.

Алгоритм перехода от таблицы истинности логической функции к ее записи в виде СКНФ:

1) выбрать в таблице истинности такие входные на­боры, на которых функция имеет нулевые значения;

2) по каждому такому набору составить элементарные дизъюнкции максимального ранга (макстермы);

3) в макстермы записать не инвертированными переменные, заданные нулем в таблице истинности, а инвертированными - те переменные, которые в таблице истинности заданы единицей;

4) полученные макстермы соединить между собой знаками конъюнкции.

Помимо двух основных (СДНФ и СКНФ) аналитиче­ских форм представления функций в алгебре логики су­ществуют дизъюнктивные и конъюнктивные нормальные формы (ДНФ и КНФ), а также минимальные дизъюнк­тивные и конъюнктивные нормальные формы (МДНФ и МКНФ).

ДНФ/КНФ – это дизъюнкция/конъюнкция элементарных конъюнкций /дизъюнкций, ранг хотя бы одной из которых отличается от максимального ранга. ДНФ/КНФ называется минимальной, если она содержит наименьшее число букв по сравнению со всеми ДНФ/КНФ, существующими для данной функции. При помощи правил развертывания элементарных конъюнкций и дизъюнкций, ДНФ и КНФ могут быть преобразованы в СДНФ и СКНФ.

В общем виде СДНФ и СКНФ записываются выражениями (2.24) и (2.26), которые могут быть слишком громоздкими. Для их упрощения используется более компактная числовая форма записи, предусматривающая только перечисление десятичных эквивалентов двоичных наборов, на которых функция принимает значение единицы (для СДНФ) или нуля (для СКНФ), соединив их знаками дизъюнкции (для СДНФ) и конъюнкции (для СКНФ).

Пример 1. Пусть логическая функция P(x,y,z) задана следующей таблицей истинности (табл. 2.3). Требуется представить ее в виде СДНФ и СКНФ.

Решение. По таблице истинности находим, что функция P(x,y,z) принимает единичные значения на четырех входных наборах аргументов. Данным наборам аргументов соответствуют следующие четыре минтерма: , , , .

Т

огда, в виде СДНФ данная логическая функция будет представлена в следующем виде:

Таблица 2.3.

Входные наборы			Значение функции	для СДНФ	для СКНФ
z	y	x		минтерм	макстерм
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

По аналогии, представим данную логическую функцию в виде СКНФ. В итоге получим:

Задание N2.4.

1. Представить в виде СДНФ и СКНФ логические функции, заданные табл. 2.2, которая является таблицей истинности этих функций.

2. Для приведенных ниже функций построить их СДНФ и СКНФ.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

Контрольные вопросы:

2.4.1. Как построить на основе таблицы истинности СДНФ функции?

2.4.2. Как построить на основе таблицы истинности СКНФ функции?

2.4.3. Что такое аналитическая форма представления логической функции? Какие преимущества она имеет перед табличной формой?

2.6.4. Геометрическая и кубическая формы представления логических функций

В геометрическом смысле каждый двоичный набор

(a₁ a₂.... a_n) переменных логической функции можно рассматривать как n-мерный вектор, определяющий точку n-мерного пространства. Исходя из этого, все множество наборов, на которых определена функция n переменных, представля­ется в видe вершин n-мерного куба. Отмечая точками вершины, в которых функция имеет единичные значения, получают ее геометрическое представление, например так, как показано на рис. 2.3, а.

а) б ) в)

Рис. 2.3. Геометрическое и кубическое представление функции Y= (3,4,5,6,7): a — 0-кубы; б — 1-кубы; в — 2-куб

На основе геометрических представлений строятся ку­бические представления логических функций, в которых используются элементы n-мерных кубов. Геометрически каждому набору (a₁ a₂.... a_n) соответствует вершина n-мерного куба с данными координатами. Каждую вер­шину, на которой функция принимает единичное значе­ние, принято называть 0-кубом (нулевым кубом). Множество 0-кубов образует нулевой кубический комплекс Ко. Например, для функции Y = V(3, 4, 5, 6, 7) нулевой ку­бический комплекс имеет вид Ко = (011, 100 101, 110, 111) и в данном случае состоит из пяти 0-кубов, каждый из которых соответствует определенной вершине трехмерного куба (рис. 2.3, а).

Если два 0-куба из комплекса К₀ различаются только по одной координате, то они образуют один 1-куб (еди­ничный куб). Он представляется общими элементами 0-кубoв, а на месте координаты, по которой различаются 0-кубы, указывается символ «-», обозначающий независимую координату. Например, два 0-куба: 100, 101 разли­чаются только по третьей координате и, следовательно, образуют единичный куб 10-, которому соответствует ребро трехмерного куба. Все множество единичных кубов функции образует единичный кубический комплекс К_1. Для функции Y =V(3, 4, 5, 6, 7) он состоит из пяти 1-кубов: K₁ ={-11, 10-, 1-0, 1-1, 11-} и определяет все множество ребер, на которых функция Y принимает единичные значения (рис. 2.3,б).

Если два единичных куба из комплекса K₁ имеют общую независимую координату и различаются только по одной координате, то они образуют один 2-куб (двоич­ный куб). Его запись состоит из общих компонент 1-ку­бов, а координата, принимающая различные значения в 1-кубах, обозначается в 2-кубе как независимая коор­дината «-» (пробел). Например, два единичных куба 1-0 и 1-1 образуют один двоичный куб 1--. Для рассмат­риваемой функции Y двоичный комплекс имеет вид К₂ ={1--} и состоит из одного двоичного куба, соответствующего грани трехмерного куба (рис. 2.3, в). Размерность куба определяется числом независимых; координат (символов «-»).

Объединение кубических комплексов К₀, К₁, … К_n функции f(x₁, x₂,…,x_n) образует кубический комплекс функции К(f). Для рассматриваемого примера комплекс К(f) соответствует объединению комплексов К₀ , К₁ и К₂.

В отличие от аналитических форм записи логических функций, где используется большой набор индексированных букв и математических знаков, кубические представления позволяют задавать логические функции в виде множества кубов, компонентами которых являются только три символа; 0, 1, - . Ограниченное число символов в записи функций позволяет использовать кубические представления в ЭВМ при решении задач автоматизированного логического проектирования комбинационных автоматов.

Задание N2.5.

1.Геометрически представить функции, заданные табл. 2.2, которая является таблицей истинности этих функций.

2. Найти кубический комплекс K(F_i) для каждой логической функции F_i (x₀, x₁, x₂), где i=0,…,9, заданной таблицей истинности 2.2.

Контрольные вопросы:

2.5.1. Что такое кубический комплекс логической функции?

2.5.2. Чем отличается геометрическая форма представления логической функции от кубической?

Лабораторная работа N3

Цель работы: изучение способа представления закона функционирования комбинационного автомата с помощью временной диаграммы.

3. ЗАДАНИЕ ЗАКОНА ФУНКЦИОНИРОВАНИЯ ЦИФРОВЫХ АВТОМАТОВ ПОСРЕДСТВОМ ВРЕМЕННЫХ ДИАГРАММ.

Временная диаграмма – это, по сути, упрощенный график изменения во времени токов или напряжений, характеризующих некоторый электрический процесс.

По горизонтали на временной диаграмме располагают ось времени, а по вертикали - ось напряжений или токов. Время увеличивается слева направо, то есть из двух событий то, которое отображается правее, является и более поздним. Такое расположение и направление оси времени традиционное и используется также во всех осциллографах – приборах, которые чаще всего применяют в инженерной практике при проектировании, отладке и эксплуатации цифровых автоматов.

Временные диаграммы являются эффективным способом визуализации (зрительного представления) динамики работы дискретных автоматов, а также международным языком, поясняющим особенности закона функционирования цифровых автоматов.

Т

ак как современные цифровые автоматы используют двоичный структурный алфавит, то для физического представления символов такого алфавита используют два, существенно различных уровня напряжения: один уровень напряжения - для представления логической 1, а другой - логического 0.

Если для представления логической 1 используют более высокий уровень напряжения, то принято говорить, что такой автомат функционирует в положительной (позитивной) логике. Если же за логическую 1 принимают более низкий уровень напряжения, то принято говорить, что автомат функционирует в отрицательной (негативной) логике. При изложении дальнейшего материала считается, что речь идет об автоматах, функционирующих в положительной (позитивной) логике.

В природе не существует идеальных дискретных явлений или процессов, поэтому реальный дискретный сигнал есть аналоговый (непрерывный) сигнал, специальной формы, который и принимается за дискретный сигнал.

Дискретные сигналы выглядят на экране осциллографа примерно так, как показано на рис. 3.1(а), а идеализированное их представление соответствует рис. 3.1(б).

Рис. 3.1. Формы дискретных сигналов

а) на экране осциллографа; б) условное графическое изображение (пунктиром показано изображение идеального дискретного сигнала).

Ранее отмечалось, что дискретные сигналы могут быть "короткими" (как в автомате типа Мили), и "длинными" (как в автомате типа Мура). В инженерной практике в среде разработчиков цифровой аппаратуры вместо терминов "короткие" и "длинные" сигналы используют термины "импульс" и "потенциал", соответственно [4].

Под импульсом понимают цифровой сигнал, длительность которого является его характеристикой. Для импульсного сигнала задана его временная характеристика (длительность), отклонение значения которой незначительны относительно некоторой заданной величины.

Под потенциалом понимают сигнал, длительность которого не регламентирована.

Возможны и иные инженерные трактовки импульса и потенциала, например, на основе сопоставления их длительностей относительно периода следования сигналов синхронизации, генерируемых самым высокочастотным генератором цифрового автомата. В этом случае, импульсным сигналом считается любой сигнал, длительность которого не превосходит периода следования тактовых импульсов от самого высокочастотного генератора. Все другие сигналы относят к потенциальным сигналам.

Иногда под импульсным сигналом понимают любой исполнительный сигнал, то есть тот, воздействие которого непосредственно приводит к исполнению некоторой процедуры. Под потенциальным сигналом, в этом случае, понимают сигнал, подготавливающий или разрешающий/запрещающий некоторое действие.

Приведенные определения импульса и потенциала не совпадают с общепринятыми определениями в электронике и импульсной технике, но весьма продуктивны в инженерной практике и, в частности, для "чтения" временных диаграмм.

Задание N3.

Для логических функций, заданных ниже в виде СДНФ или СКНФ построить:

а) таблицу истинности;

б) карту Карно;

в) временную диаграмму.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

Контрольные вопросы:

3.1. Как с помощью временной диаграммы задать цифровой автомат?

3.2. Сформулируйте определение импульса и потенциала.

Лабораторная работа N4

Цель работы: изучение алгоритма синтеза комбинационного автомата на основе логических элементов.

4. ПРОЕКТИРОВАНИЕ ЛОГИЧЕСКИХ СХЕМ С ПОМОЩЬЮ ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ.

Логической схемой называется совокупность логических электронных элементов, соединенных между собой таким образом, чтобы выполнялся заданный закон функционирования схемы, иначе говоря, - выполнялась заданная логическая функция.

По зависимости выходного сигнала от входного все электронные логические схемы можно условно разбить на:

схемы первого рода, т.е. комбинационные схемы, выходной сигнал которых зависит только от состояния входных синалов в каждый момент времени;

схемы второго рода или накапливающие схемы (схемы последовательностные), содержащие накапливающие схемы (элементы с памятью), выходной сигнал которых зависит как от входных сигналов, так и от состояния схемы в предыдущие моменты времени.

По количеству входов и выходов схемы бывают: с одним входом и одним выходом, с несколькими входами и одним выходом, с одним входом и несколькими выходами, с несколькими входами и выходами.

По способу осуществления синхронизации схемы бывают с внешней синхронизацией (синхронные автоматы), с внутренней синхронизацией (асинхронные автоматы являются их частным случаем).

Практически любой компьютер состоит из комбинации схем первого и второго родов разной сложности. Таким образом, основой любого цифрового автомата, обрабатывающего цифровую информацию, являются электронные элементы двух типов: логические или комбинационные и запоминающие. Логические элементы выполняют простейшие логические операции над цифровой информацией, а запоминающие служат для ее хранения. Как мы уже знаем, логическая операция состоит в преобразовании по определенным правилам входной цифровой информации в выходную.

Можно считать, что элементарные логические функции являются логическими операторами упомянутых электронных элементов, т.е. схем. Каждая такая схема обозначается определенным графическим символом. Приведем примеры графического обозначения этих схем (рис.4.1).

Рис. 1

Рис. 4.1. Графическое обозначение логических элементов

Рассмотрим пример.

Синтезировать логическую схему, реализующую логическую функцию , с помощью логических элементов, изображенных на рис.4.1 .

Задание N4.

Синтезировать логическую схему, реализующую следующие логические функции:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

с помощью логических элементов, изображенных на рис.4.1 .

Контрольные вопросы:

4.1. Что такое логическая схема?

4.2. По каким принципам можно классифицировать логические схемы?

4.3. Что такое логические операторы?

Лабораторная работа N5

Цель работы: изучение понятий функционально полных базисов и их функциональной полноты.

5. ПОНЯТИЕ ЭЛЕМЕНТНОГО БАЗИСА И ИХ ОСНОВНЫЕ РАЗНОВИДНОСТИ.

Любую логическую функцию в алгебре логики можно представить в виде СДНФ и СКНФ, используя три элементарные логические функции: инверсию, конъюнкцию и дизъюнкцию. Данный набор представляет собой полный функциональный набор.

Система функций алгебры логики f₁, f₂, …, f_m называется функционально полной, если любая логическая функция от произвольного числа n – аргументов может быть представлена суперпозицией функций f₁, f₂, …, f_m.

Система логических функций, обладающая функциональной полнотой, называется функциональным базисом, а набор элементов, реализующих эти функции, называется элементным базисом.

Минимальным базисом называется такой базис из f₁, f₂, …, f_n, для которого удаление хотя бы одной из функций f_i, входящих в этот базис, превращает систему функций f₁, f₂, …, f_m в неполную.

Если осуществить преобразования над логическими функциями, заданными СДНФ и СКНФ по правилам де Моргана, взяв от них двойное отрицание, то получим функционально полные базисы, состоящие из одной или двух элементарных функций.

Функциональной полнотой обладают следующие элементные базисы:

1. И, ИЛИ, НЕ (основной базис);

2. И, НЕ;

3. ИЛИ, НЕ;

4. И-НЕ;

5. ИЛИ-НЕ;

6. 1, И, .

Для определения функционально полных систем логических функций необходимо для них определить наличие следующих пяти свойств:

1. Свойство сохранения нуля: данным свойством обладают те логические функции, для которых справедливо соотношение:, т.е. на нулевом наборе аргументов, логическая функция принимает нулевые значения.

2. Свойство сохранения единицы: данным свойством обладают те логические функции, для которых справедливо соотношение:, т.е. на единичном наборе аргументов, логическая функция принимает единичные значения.

3. Свойство самодвойственности: данным свойством обладают те логические функции, для которых справедливо соотношение:, т.е. самодвойственной является функция, у которой инвертирование значений всех аргументов приводит к инвертированию значений функции.

4. Свойство монотонности: функция обладает этим свойством, если для любой последовательности наборов, в каждом из которых аргументы не убывают, значения функции также не убывают, при этом полагаем, что 0<1.

5. Свойство линейности: данным свойством обладают те логические функции, которые могут быть представлены в следующем виде:

, где .

Теорема Поста: Для того, чтобы множество N двоичных функций было базисом необходимо и достаточно, чтобы:

1. N содержало бы по крайней мере одну функцию, не сохраняющую ноль;

2. N содержало бы по крайней мере одну функцию, не сохраняющую единицу;

3. N содержало бы по крайней мере одну функцию, немонотонную;

4. N содержало бы по крайней мере одну функцию, несамодвойственную;

5. N содержало бы по крайней мере одну нелинейную функцию.

Задание N5.1.

Воспользовавшись теоремой Поста доказать, что следующие системы функций являются функционально полными или неполными системами:

1. ;

2. ;

3.

4.

5. где- операция штрих Шеффера (И-НЕ).

6.

7. где- операция эквиваленции.

8. где- операция эквиваленции.

9. где- операция стрелка Пирса (ИЛИ-НЕ).

10.

Контрольные вопросы:

5.1. Сформулируйте определение функционально полной системы функций алгебры логики.

5.2. Перечислите свойства элементарных логических функций, влияющих на формирование функционально полных логических базисов.

5.3. Сформулируйте теорему Поста.

Лабораторная работа N6

Цель работы: получение практических навыков реализации логических функций в различных функциональных базисах.

6. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ В БАЗИСАХ И-НЕ, ИЛИ-НЕ ПО КНФ И ДНФ.

Для того, чтобы реализовать логическую функцию, заданную в ДНФ в базисе И-НЕ необходимо взять двойное отрицание от этой функции и по законам де Моргана заменить все дизъюнкции на конъюнкции, т.е.:

.

Для того, чтобы реализовать логическую функцию, заданную в ДНФ в базисе ИЛИ-НЕ необходимо взять четверное отрицание от этой функции и по законам де Моргана заменить все дизъюнкции на конъюнкции, т.е.:

.

Для того, чтобы реализовать логическую функцию, заданную в КНФ в базисе ИЛИ-НЕ необходимо взять двойное отрицание от этой функции и по законам де Моргана заменить все конъюнкции на дизъюнкции, т.е.:

.

Для того, чтобы реализовать логическую функцию, заданную в КНФ в базисе И-НЕ необходимо взять четверное отрицание от этой функции и по законам де Моргана заменить все конъюнкции на дизъюнкции, т.е.:

.

Задание N6.

Реализовать в элементных базисах ИЛИ-НЕ и И-НЕ следующие функции и построить их логические схемы:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

Контрольные вопросы:

6.1. Перечислите известные Вам функциональные базисы.

6.2. Как реализовать в базисах И-НЕ, ИЛИ-НЕ инверсию одной переменной?

6.3. Можно ли по полученной логической схеме в базисе И-НЕ узнать, в каком виде первоначально была задана логическая функция (в ДНФ или в КНФ)?

Лабораторная работа N7

Цель работы: получение практических навыков минимизации логических функций с помощью методов Квайна, карт Карно, испытания импликант, импликантных матриц.

7. МИНИМИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ.

Сложность логической функции, а отсюда сложность и стоимость реализующей ее схемы (цепи), пропорциональны числу логических операций и числу вхождений переменных или их отрицаний. В принципе любая логическая функция может быть упрощена непосредственно с помощью аксиом и теорем логики, но, как правило, такие преобразования требуют громоздких выкладок. К тому же процесс упрощения булевых выражений не является алгоритмическим. Поэтому более целесообразно использовать специальные алгоритмические методы минимизации, позволяющие проводить упрощение функции более просто, быстро и безошибочно. К таким метода относятся, например, метод Квайна, метод карт Карно, метод испытания импликант, метод импликантных матриц, метод Квайна-Мак-Класки и др. Эти методы наиболее пригодны для обычной практики, особенно минимизация логической функции с использованием карт Карно. Метод карт Карно сохраняет наглядность при числе переменных не более шести. В тех случаях, когда число аргументов больше шести, обычно используют метод Квайна-Мак-Класки.

В процессе минимизации той или иной логической функции, обычно учитывается, в каком базисе эффективнее будет реализовать ее минимальную форму при помощи электронных схем.

Более подробно вопросы минимизации логических функций рассматриваются на лекционных занятиях по дисциплине “Теория автоматов”.

Задание N7.

1. Воспользовавшись лекционными материалами по данной дисциплине минимизировать следующие логические функции методом Квайна, методом испытания импликант, методом импликантных матриц, методом карт Карно и сравнить полученные минимизированные формы:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

2. Построить логические схемы, реализующие полученные минимизированные формы и оценить их стоимость.

Контрольные вопросы:

7.1. В чем состоит метод Квайна?

7.2. Сформулируйте достоинства и недостатки метода карт Карно.

7.3. Что такое импликанта и импликантная матрица?

Лабораторная работа N8

Цель работы: получение практических навыков в реализации функциональных преобразователей на основе дешифратора.

8. ИССЛЕДОВАНИЕ ДЕШИФРАТОРОВ.

Дешифратор - это комбинационное устройство, позволяющее распознавать числа, представленные позиционным n-разрядным кодом. Если на входе дешифратора n-разрядный двоичный код, то на его выходе код “1 из N”. В кодовой комбинации этого кода только одна позиция занята единицей, а все остальные – нулевые.

Дешифратор предназначен для преобразования n-разрядного позиционного кода в k-разрядный унитарный код, при этом число входов n<k.

Если , то такой дешифратор называется полным, если, дешифратор называется неполным.

Более подробно принципы синтеза комбинационных автоматов рассматриваются на лекционных занятиях по дисциплине “Теория автоматов”.

Задание N8.

Воспользовавшись лекционным материалом по данной теме, реализуйте следующие логические функции на полном дешифраторе, предварительно представив их в СДНФ, т.е. составьте таблицы истинности и функциональные схемы работы дешифратора:

1. 6.

2. 7.

3. 8.

4. 9.

5. 10.

Контрольные вопросы:

8.1. К классу каких автоматов относится дешифратор?

8.2. Сформулируйте определение дешифратора и опишите его представление на уровне "черного ящика" или в виде nk – полюсника.

8.3. Перечислите основные этапы последовательности синтеза комбинационных автоматов.

Лабораторная работа N9

Цель работы: получение практических навыков по реализации функциональных преобразователей на основе программируемых пользователем логических матрицах (ППЛМ).

9. ПРОГРАММИРУЕМЫЕ ПОЛЬЗОВАТЕЛЕМ ЛОГИЧЕСКИЕ МАТРИЦЫ.

Создание двухуровневых программируемых пользователем логических матриц (ППЛМ) было ответом производителей цифровых интегральных микросхем на сложившуюся в конце 60-х годов прошлого века парадоксальную ситуацию: разновидностей логических микросхем требовалось все больше и больше, а объемы производства каждой разновидности постоянно снижались. В такой ситуации был найден, возможно, единственно правильный выход, который заключался в разработке и массовом выпуске достаточно универсальных интегральных микросхем, которые могли использоваться и в единичных экземплярах, но миллионами индивидуальных пользователей. Именно таким образом обеспечивался компромисс между большими затратами на организацию массового производства некоторого типа интегральных микросхем и быструю окупаемость этих затрат.

Т

акими интегральными микросхемами и стали, так называемые ныне, двухуровневые программируемые пользователем логические матрицы. Эти интегральные микросхемы позволяют (при наличии у пользователя специальных программаторов) оперативно реализовывать достаточно сложные многовыходные логические преобразователи (ЛП), закон функционирования которых изначально представляется в естественной для человека форме. Строгое математическое выражение этой естественной формы в научно-технической литературе принято называть совершенной дизъюнктивной нормальной формой (СДНФ) или ее минимизированным эквивалентом – дизъюнктивной нормальной формой (ДНФ). Универсализм двухуровневых ППЛМ обеспечивается введением на этапе их серийного производства значительной структурной избыточности как электронных элементов ППЛМ, так и электрических связей между этими элементами. При этом в архитектуру ППЛМ вводятся дополнительные электронные узлы, обеспечивающие по командам извне разрушение в определенных местах ненужных электрических связей между избыточными элементами, образующими собственно ППЛМ. Схема электрическая функциональная незапрограммированной ППЛМ показана на рис. 9.1.

Как видно из рис.9.1 ППЛМ состоит из блока инверторов (DD₁...DD_S) входных логических переменных (X₁...X_S) и двух матриц.

Матрица И реализует на шинах Z₁...Z_q элементарные конъюнкции с любым набором прямых и инверсных значений логических переменных X₁...X_S, а матрица ИЛИ реализует элементарные дизъюнкции с элементарными конъюнкциями, сформированными на шинах Z₁...Z_q. Результат операций дизъюнкции формируется на выходных шинах Y₁...Y_t.

Матрицы И и ИЛИ представляют собой систему ортогональных проводников, в узлах пересечения которых располагаются полупроводниковые элементы, реализующие с резисторами нагрузки операции И и ИЛИ. Операцию И реализуют при помощи диодов, а операцию ИЛИ – при помощи триодов.

Электрическое подключение диодов и триодов к соответствующим ортогональным проводникам осуществляется через специальные перемычки P_i (P_j), некоторые из которых при программировании ППЛМ удаляются (пережигаются) в соответствующих узлах. На рис. 9.2 показано подключение диодов в узлах матрицы И, а на рис. 9.3 – подключение триодов в узлах матрицы ИЛИ.

Логические уравнения для выходных сигналов Y₁...Y_t , формируемых незапрограммированными ППЛМ, имеют один и тот же вид в СДНФ:

(9.1)

где r =;

- операция логического сложения (дизъюнкция);

- операция логического умножения (конъюнкция).

Рис. 9.1. Схема электрическая функциональная незапрограммированной ППЛМ (без дополнительных электронных узлов)

Рис. 9.3. Подключение триодов в узлах матрицы ИЛИ

C

хема электрическая функциональная запрограммированной ППЛМ изображается примерно так же, как представлено на рис. 9.1. Отличие состоит в том, что метки () на схеме проставляют только в тех узлах матрицы ППЛМ, в которых должны быть подключены диоды и транзисторы, обеспечивающие реализацию логических уравнений.

Задание N9.

Реализовать следующие логические функции на ПЛМ.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

Контрольные вопросы:

9.1. Какими причинами вызвано создание двухуровневых программируемых пользователем логических матриц?

9.2. Из каких матриц состоит ППЛМ, назначение этих матриц.

9.3. Как осуществляется программирование матрицы?

9.4. Какой вид имеют логические уравнения выходных сигналовY_t, формируемых незапрограммированными ППЛМ?

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Сикорский Р. Булевы алгебры. – М.: Мир, 1969. - 376с.

2. Яглом И.М. Булева структура и ее модели. – М.: Сов. радио, 1980. - 192с.

3. Киносита К., Асада К., Карацу О. Логическое проектирование СБИС. – М.: Мир, 1988. - 309с.

4. Завадский В.А. Компьютерная электроника. - Киев: ВЕК, 1996. - 368с.

5. Лачин В.И., Савелов Н.С. Учебное пособие.4-е изд. – Ростов н/Д: Феникс, 2004. – 576с.

6. Новожилов О.П. Основы цифровой техники/Учебное пособие.- М.: ИП РадиоСофт, 2004. – 528с.

ПРАКТИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ АВТОМАТОВ

методические указания

к выполнению лабораторных работ № 1-9

по дисциплине «Теория автоматов» для студентов 230101

очной формы обучения

Составители:

Акинина Юлия Сергеевна

Тюрин Сергей Владимирович

В авторской редакции

Подписано в печать 01.12. 05. Формат 60x84/16.

Бумага для множительных аппаратов. Усл. печ. л. 3,6.

Уч.-изд.л.3,1. Тираж 100 экз. “С”

Заказ № .

Воронежский государственный технический университет