13. Метод установления для уравнения эллиптического типа. Единственность решения.

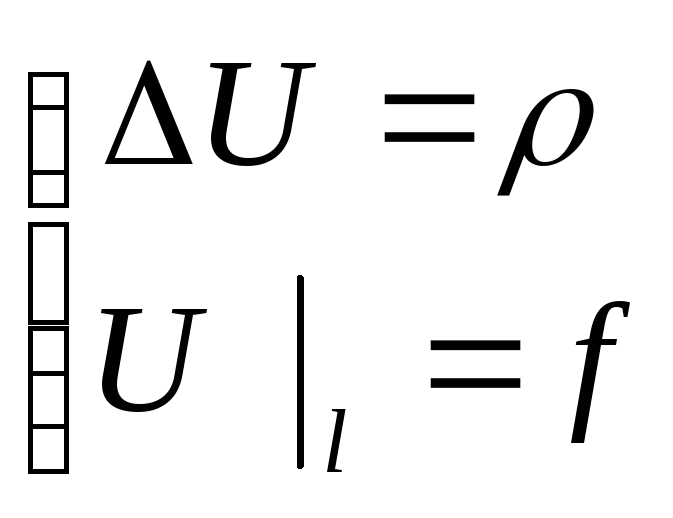
Пусть в некоторой области Ѕ необходимо решить первую краевую задачу для уравнения Пуассона:На ряду с ней рассмотрим эволюционную задачу: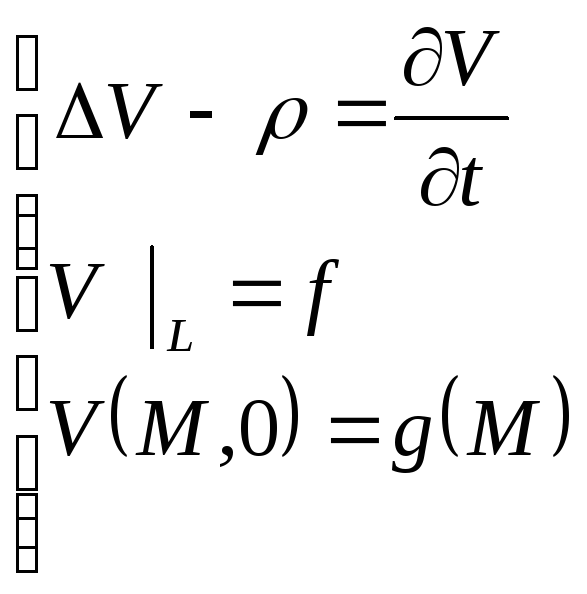гдеg(M) – произвольная функция, удовлетворяющая краевым условиям задачи (1). Покажем, что при асимптотически, то есть рассмотрим задачу: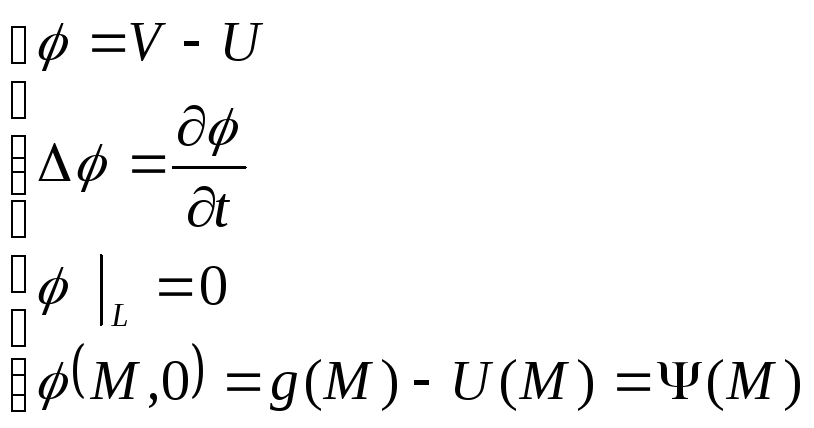где- произвольная функция, удовлетворяющая задачи Коши. Будет показано, что решение задачи (3) представимо в ви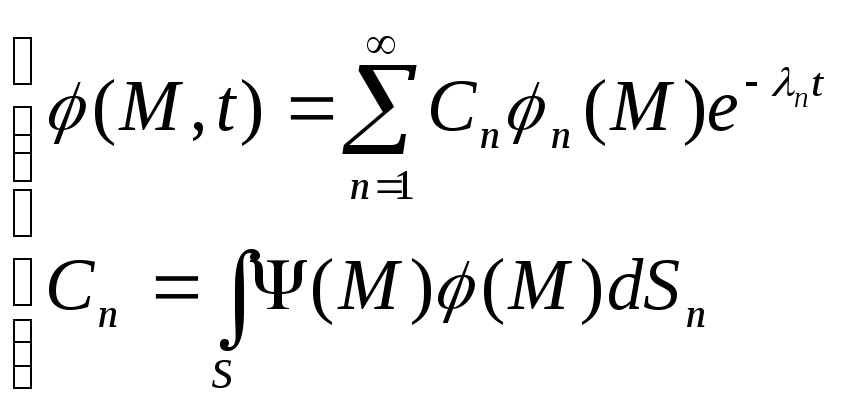де:где- коэффициенты Фурье, аи- решение следующей задачи Штурма-Лиувилля: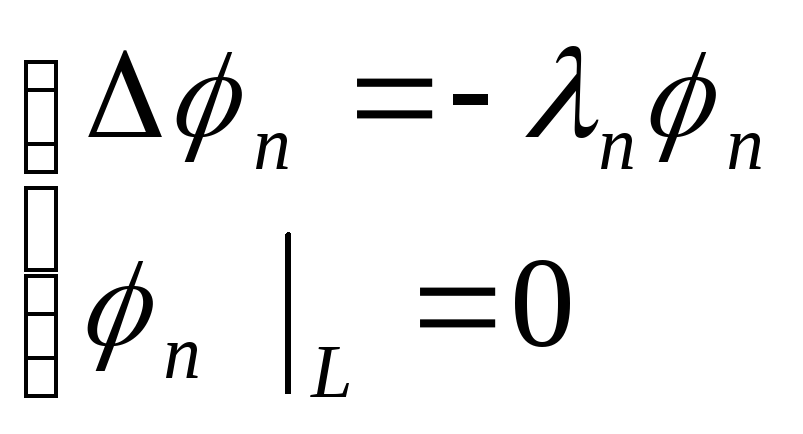Причем- образуют полную ортогональную систему функций, которую можно нормировать так, что будет выполняться равенство:Из свойств собственных функций и собственных чисел можно построить сумму:Из теории рядов Фурье известно, что, тогда устремляя в последнем неравенстве, получаем:

Стремление быстрое, так как в оценке существует экспонента, поэтому уже при малых временах решение получается с хорошей точностью.

14 Численная реализация метода установления для уравнения Пуассона. Устойчивость и скорость сходимости.

Рассмотрим особенности численного решения эллиптического уравнения на примере уравнения Пуассона. Для удобства ограничимся двумерной задачей Дирихле в квадратной области

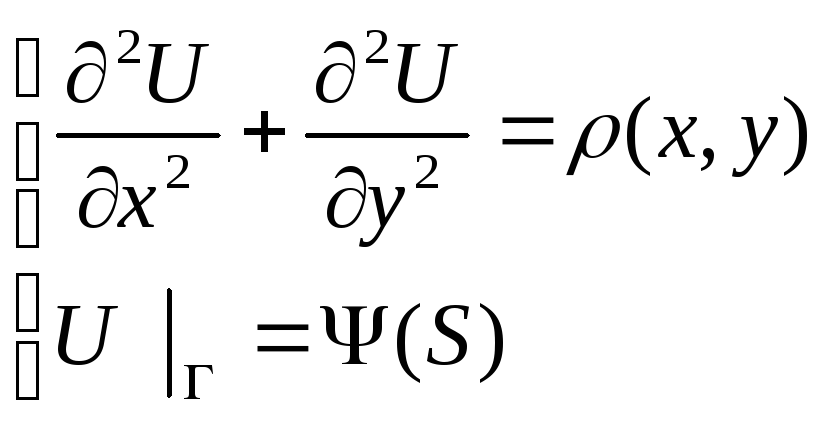
гдеS– длина дуги, отсчитываемая вдоль границы,и- заданные функции.Введем квадратную сеткуцелое число. Запишем конечно-разностный аналог уравнения (1), заменяя вторые производные стандартной трёхточечной аппроксимацией: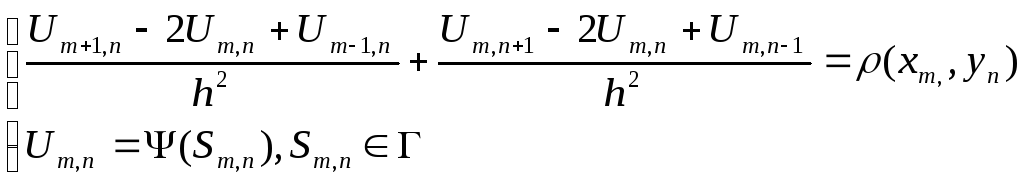Схема (2) есть СЛАУ относительноРешить систему (2) каким либо общим методом численной линейной алгебры (метод Гаусса) невыгодно, т.к. такой метод не учитывает сильную разреженность матрицы системы (2) (действительно, из общего числанеизвестных только 5 содержаться в каждом из уравнений (2)) и поэтому оказывается чересчур медленным. Вместо этого используются специальные методы: прямые или итерационные. Итерационные методы менее быстрые, чем прямые, но за то более универсальны, т.к. не зависят от геометрии расчетной области и легче программируются.В данном случае рассматривается итерационный подход, эквивалентный расчету на установление развивающегося во времени процесса. Рассмотрим вспомогательную нестационарную залачу:

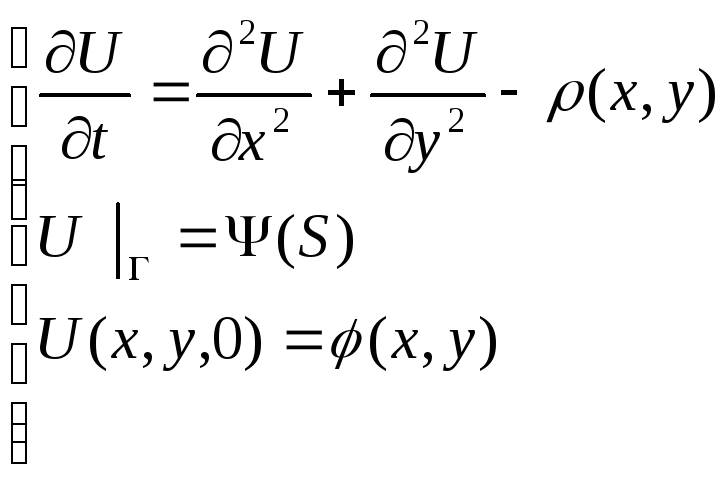
гдеи- те же самые, что и в (1), а- произвольно. Решение задачи (3) пристремится к равновесному распределению, опнсываемому задачей (1), В соответствии с этим вместо (1) будем решать (3), а вместо равновесной схемы введем схему:

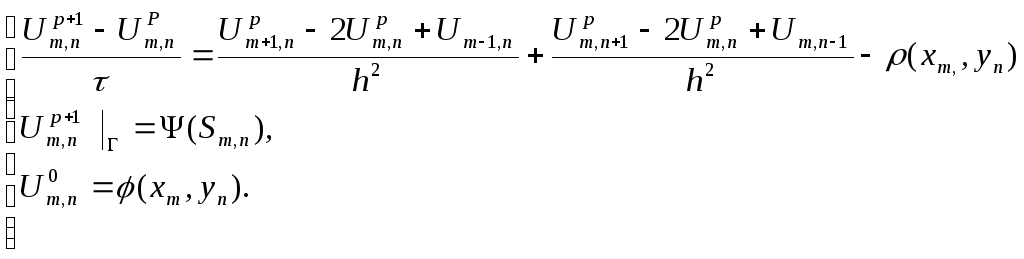
Вычислениепо уже известнымв данной схеме (4) не составляет труда. Можно показать, что наибольшая сходимость достигается в случая:Схема (4) с выбором оптимального “временного шага” согласно (5) называется схемой Якоби и является простейшей из итерационных схем.Для квадратной области число итераций, необходимых для достижения заданной точности приравно:Сходимость итераций по схеме (4)-(5)имеет место и в случае расчетной области произвольной сложной формы. Схема (4) выдерживает обобщение на случай задачи Дирихле с переменными коэффициентами.

15. Волновое ур-е. Начал и краевые усл-я для волнового ур-я.Волновое уравнение можно записать в таком виде:∆φ-1/a²∂²φ/∂t²=f(M,t),aопределяет скорость распространения волны,или спользуя оператор Даламбера:□φ=f(M,t), □ – даламбериан

Волн ур-е имеет ∞ мн-во решений. Заданием краев и начал усл выделяется конкретное реш-е. Краевые усл-я для волн ур-я ставятся также как и для ур-я Лапласа. Начал усл заключаются в задании распределения ф-ции и ее перв производной и имеют вид: / φ(M,0)=f₁(M)\ ∂φ/∂t(M,0)=f₂(M)Совок волн ур-я, краевых и начал усл отражает начально-краевую задачу для волн ур-я.