
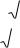
К характеристикам меры рассеяния (амплитуды рассеяния) относятся дисперсия, среднеквадратическое отклонение, коэффициент вариации и вариационный размах R.
R=X max−X min |
|
|
|
|
|
|
|
Отсев грубых погрешностей при |
n ≤ 25 : |
|
|
xi − x |
|
|
≤ τ1− p (τ1p – табличное |
|
|
|
|
||||
|
|
||||||
|
|
S |
|
|
|||
|
|
|
|
|
|
|
|
значение критерия Стьюдента). |
|
|
|
|
|
|
|
2. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
Корреляционный анализ (корреляционная модель ) метод, применяемый тогда, когда данные наблюдений или эксперимента можно считать случайными и выбранными из совокупности, распределенной по многомерному нормальному закону .
Изображение точек выборки ( x1 , y1 ) , ( x2 , y2 ) ,…, ( xn , yn ) на координатной плоскости корреляционное поле.
Мерой линейной статистической связи двух случайных величин, имеющих нормальное распределение, является коэффициент парной корреляции. Выборочный парный коэффициент корреляции
определяется по формуле:
|
|
|
n |
|
|
|
n |
|
n |
|
|
|
|
|
|
|
|
n ∑ x i y i −∑ x i ∑ y i |
|
|
|
||||||||||
r x y = |
|
|
i=1 |
|
|
i =1 |
i=1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
n |
|
2 |
n |
|
|
|
n |
|
2 |
||||
|
n x 2 |
− |
∑ |
x |
n |
|
y |
2 |
− |
y |
|||||
|
∑ i |
|
i |
|
∑ |
|
i |
∑ |
i |
|
|
||||
|
i=1 |
|
i=1 |
|
|
i=1 |
|
|
|
i=1 |
|
|
|
||
Проверка на значимость. Гипотезы: H0 : r = 0 ; H1 : r ¹ 0
При справедливости гипотезы H0 статистика критерия t = |
|
r |
|
|
n − 2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
1− r2 |
|||||||
|
|
|
||||||
имеет tраспределение Стьюдента с (n2) степенями свободы. |
|
|
|
|
|
|
|
|
Гипотеза H0 отвергается, то есть выборочный коэффициент |
||||||||
корреляции значимо отличается от нуля, если tрасч. > tα ,n−2 , |
где tα ,n−2 |
|||||||
табличное значение критерия Стьюдента, определённое на уровне значимости α при числе степеней свободы (n2).

Доверительный интервал (интервальная оценка) значимого коэффициента корреляции p = r ± uα 1−nr2 ,
где uα критическая точка стандартного нормального распределения, соответствующая уровню значимости α, n объем выборки.
В случае нелинейной зависимости тесноту связи между величинами оценивают по величине корреляционного отношения.
|
|
n |
|
|
|
|
|
|
|
|
|
∑ yi−yi |
2 |
|
значения, а yi |
||||
R= 1− |
i=1 |
|
|
|
|
, где yi |
наблюдаемые |
||
расчётные |
|
n |
i |
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|||
|
|
y |
−y 2 |
|
|
||||
|
i=1 |
|
|
|
|
|
|
|
|
значения зависимого признака, которые вычисляют на основе |
|||||||||
уравнения |
|
парной |
|
регрессии |
yi= f xi . Интервал изменения |
||||
|
|
|
|
|
|
|
|
|
|
корреляционного отношения 0 R 1 |
|
||||||||
Величина |
|
R2 |
, |
называемая |
коэффициентом |
детерминации, |
|||
показывает, какая часть общей вариации Y обусловлена вариацией X. Проверка значимости корреляционного отношения η основана на том,
что статистика |
F = |
R2 n− p−1 |
|
(p – число факторов, n – количество |
|
1−R2 p |
|||||
|
|
|
|||
наблюдений) имеет F распределение Фишера Снедекора с k1= p и |
|||||
k2=n− p−1 |
степенями свободы. Поэтому η значимо отличается от |
||||
нуля, если F F ,k 1 , k2 , где F ,k 1 , k2 табличное значение F критерия
на уровне значимости α при числе степеней свободы k1 и |
k2 . |
|
МНОЖЕСТВЕННЫЙ КОРРЕЛЯЦИОННЫЙ АНАЛИЗ |
|
|
Пусть имеется совокупность случайных переменных X1 , |
X 2 ,…, |
Xi , |
…, X j , …, X p имеющих совместное нормальное распределение. |
|
|
Матрица Q составленная из парных коэффициентов корреляции |
rij , |
|
где j, i = 1, 2, …, p, называется корреляционной: |
|
|
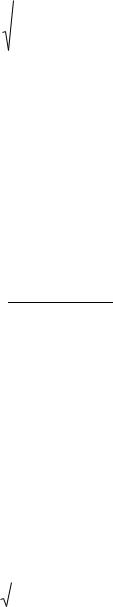
1 |
r 12 |
r13 |
... |
r 1p |
|||
r 21 |
1 |
r23 |
... |
r 2p |
|||
Q= r |
31 |
r |
32 |
1 |
... |
r |
3p |
|
|
|
|
|
|||
... ... ... ... ... |
|||||||
r p1 |
r p2 |
r p3 |
... |
1 |
|||
Теснота линейной взаимосвязи одной переменной Xi с совокупностью других (p – 1) переменных, рассматриваемой в целом, измеряется с помощью выборочного коэффициента множественной корреляции Ri
(i=1,…, p):
|
|
|
|
|
|
Ri = 1- |
Q |
|
, где Q определитель корреляционной матрицы, Qii – |
||
Q |
|||||
|
|
|
|
||
|
|
ii |
|
|
|
алгебраическое дополнение корреляционной матрицы ( 0 ≤ R ≤1).
Величина R2, называемая выборочным множественным коэффициентом детерминации, показывает, какую долю вариации исследуемой переменной объясняет вариация остальных переменных.
Коэффициент множественной корреляции значимо отличается от нуля, если значение статистики F F , где F (критерий Фишера) рассчитывается по формуле:
F = R2 n− p−1 |
|
1−R2 p |
|
n объем выборки; |
|
p количество переменных; |
|
F , k1 ,k 2 табличное значение F критерия на уровне значимости α |
|
при числе степеней свободы k1 |
и k 2 . |
Выборочным частным |
коэффициентом корреляции между |
переменными Xi и Xj при фиксированных значениях остальных (p2) переменных называется выражение:
rij = |
|
− Qij |
|
|
|
|
|
Qii ×Qjj |
|
||
|
|
|

где Qij, Qii и Qjj алгебраические дополнения соответствующих элементов матрицы парных коэффициентов корреляции.
Проверка значимости частного коэффициента корреляции осуществляется также, как парного коэффициента корреляции, только (n – 2) при этом заменяется на (n p), т. е. вычисляется статистика Стьюдента:
t = |
|
|
rij |
|
|
|
|
n − p |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1− r 2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
ij |
|
|
|
|
|
|
|
|
|||
где n количество наблюдений; p количество факторов. |
|||||||||||||||||||
Коэффициент |
частной корреляции |
считается |
значимым, если |
||||||||||||||||
tрасч. > tα ,ν , |
|
где |
|
tα ,ν |
табличное |
значение |
критерия Стьюдента, |
||||||||||||
определённое |
на |
уровне |
значимости |
α |
при |
числе |
степеней свободы |
||||||||||||
=n− p . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Коэффициент ранговой корреляции Спирмена |
|
||||||||||||||||||
|
|
|
|
|
|
|
6ån (ri |
− si )2 |
|
|
|
|
|
||||||
ρ = 1− |
|
i=1 |
|
|
, |
|
|
|
|
|
|||||||||
|
n3 − n |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где ri и si ранги iтого объекта по переменным X и Y; n – число пар наблюдений.
При проверке значимости исходят из того, что в случае справедливости нулевой гипотезы об отсутствии корреляционной связи
|
|
|
|
|
|
|
t = |
ρ |
|
|
|
|
|
|
|
|
между переменными |
при |
n > 10 |
статистика |
|
n − |
2 |
|
|
имеет t |
|||||||
|
|
|
|
|
|
|
||||||||||
1− ρ |
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
распределение Стьюдента с (n2) степенями свободы. |
|
|
|
|
|
|
|
|||||||||
|
Коэффициент |
ранговой корреляции ρ значим на |
уровне |
α, если |
||||||||||||
|
tрасч. |
|
> tα ,n−2 , где |
tα ,n−2 |
|
табличное |
значение |
критерия |
Стьюдента, |
|||||||
|
|
|||||||||||||||
определённое на уровне значимости α при числе степеней свободы (n2).
3.МОДЕЛИ И МЕТОДЫ РЕГРЕССИОННОГО АНАЛИЗА
Кзадачам регрессионного анализа относятся:
1.установление формы зависимости между переменными;
2.оценка модельной функции (модельного уравнения) регрессии;
3.оценка неизвестных значений (прогноз значений) зависимой переменной.
Врегрессионном анализе рассматривается односторонняя зависимость переменной Y (её ещё называют функцией отклика,
результативным признаком, предсказываемой или объясняемой переменной) от одной или нескольких независимых переменных X
(называемых также объясняющими или предсказывающими переменными, факторными признаками).
Парная регрессионная модель y= f x , где ε случайная переменная, характеризующая отклонение от модельной функции регрессии (она также называется возмущающей или просто
возмущением).
Основные предпосылки регрессионного анализа:
1)зависимая переменная yi (или возмущение εi) есть величина случайная, а объясняющая переменная xi есть величина неслучайная;
2)математическое ожидание возмущения εi равно нулю: M(εi)=0;
3)дисперсия зависимой переменной yi (или возмущения εi) постоянна для любого i: D i = 2i ;
4)переменные yi и yj (или возмущения εi и εj) не коррелированы:
M(εi εj)=0;
5)зависимая переменная yi (или возмущение εi) есть нормально распределённая случайная величина.
Простейшая модель регрессионного анализа, когда функция f(x) линейна как по параметрам, так и по переменным xi (i=1,…,n):
yi = β0 + β1 xi + εi
Оценкой линейной модели по выборке является уравнение регрессии
y=b0 b1 x1 .
Параметры b0 и b1 определяются на основе метода наименьших квадратов (МНК) по следующим формулам:
|
|
|
|
|
xy−x y |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
b = |
|
|
|
|
|
b |
= y−b x |
, |
|
|
|||||||
|
|
|
|
2 |
|
|
|
|
|
|||||||||||
|
|
|
1 |
|
|
|
|
|
2 , |
|
|
|||||||||
|
|
|
|
|
x |
− x |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
n |
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
∑ xi |
, |
|
|
∑ yi |
, |
|
|
|
|
∑ xi yi |
, |
2 |
|
∑ xi |
|||||
|
i=1 |
|
|
i=1 |
|
|
|
|
|
i=1 |
|
|
i=1 |
|||||||
x= |
|
|
y= |
|
|
|
|
|
|
xy= |
|
|
|
|
x |
= |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Модель множественной регрессии, включающая p объясняющих переменных x1,..., xp, имеет вид: yi = β0 + β1 xi1 + β2 xi 2 + ... + β p xip + εi .
Уравнение регрессии с оценками параметров можно записать как: y=b0 b1 x1 ... bp x p .
Оценки параметров уравнения множественной регрессии b0 ,b1,b2,...,bp получают по методу наименьших квадратов:
B= X T X −1 X T Y
X T X −1 матрица, обратная матрице X T X ,
b1 B= b2
b0
...
bp
n |
∑ xi1 |
∑ xi2 |
|
∑ xi1 |
∑ xi1 |
2 |
∑ xi1 xi2 |
X T X = ∑ xi2 |
∑ xi1 xi2 |
∑ xi22 |
|
... ... |
|
... |
|
∑ xip |
∑ xi1 xip |
∑ xi2 xip |
|
∑ yi
∑ yi xi1
X T Y = ∑ yi xi2
...
∑ yi xip
...
...
...
...
...
∑xip
∑xi1 xip
∑xi2 xip
...
∑xip2
Оценки, полученные на основе применения этого метода, обладают следующими свойствами: несмещённостью (они не содержат систематических ошибок при оценивании), состоятельностью (при
n → ∞ вероятностью, как угодно близкой к 1, сходятся к оцениваемым параметрам) и эффективностью (т. е. обладают наименьшими дисперсиями среди всех возможных несмещённых оценок параметров).
Стандартизованные коэффициенты регрессии b'j и коэффициенты эластичности Э j (j=1,…,p):
b' |
=b |
|
S x |
j |
|
Эj = bj |
xj |
|
|
|
|
y |
|||||||
j S y |
|||||||||
i |
|
|
|||||||
Стандартизованный |
коэффициент |
регрессии b'j показывает, на |
|||||||
сколько величин Sy изменится в среднем зависимая переменная Y при увеличении только jой объясняющей переменной на Sxj, а коэффициент эластичности Э j на сколько процентов (от средней) изменится в среднем Y при увеличении только Xj на 1%.
Нелинейная регрессия
С позиции использования МНК различают следующие виды зависимостей:
1) функции, нелинейные по факторам, например: y=a0 a1 x2 или y=a0 a1 loga x ;
2)функции, нелинейные по параметрам, например: y = ea0 +a1x или y = aK α L1−α
3)функции, не приводимые к линейному виду.
В первом и втором случае МНК для оценки параметров модели используется после проведения линеаризующих преобразований, приводящих функцию к линейному виду. К уравнениям второго вида вначале требуется применить линеаризующее преобразование, а затем уже заменить переменные. В третьем случае, когда функцию невозможно привести к линейному виду, оценка параметров осуществляют с помощью нелинейного МНК.
Анализ вариации зависимого показателя
Общая сумма квадратов отклонений зависимой переменной:
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
∑ |
y |
i |
− y 2= |
∑ |
y |
− y |
i |
y |
i |
− y 2 |
= |
|
|
||||||||
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
||||||||||
|
|
i=1 |
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
= |
∑ |
y |
− y |
i |
2 |
∑ |
y |
i |
− y 2 2 |
∑ |
y |
− y y |
i |
− y . |
|||||||||
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
||||||
|
i=1 |
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
Сумма квадратов отклонений фактических значений от расчётных называется остаточной суммой квадратов и обозначается как
n
Q о с т=∑ y i −y i 2 . i=1
Сумма квадратов отклонений расчётных значений от среднего называется объяснённой суммой квадратов и обозначается как
n
Q о б ъ я с н=∑ y i−y 2 i=1
Третий элемент в разложении представляет собой сумму произведений объяснённой и остаточной компонент регрессии и равен нулю. В результате общая сумма квадратов раскладывается на остаточную сумму квадратов и объяснённую сумму квадратов.
Для получения оценок соответствующих дисперсий все перечисленные выше суммы квадратов делятся на соответствующие значения степеней свободы:
1)общую сумму квадратов Q на (n1) для получения оценки общей дисперсии (S2y) зависимой переменной, которая характеризует разброс значений показателя вокруг среднего;
2)объяснённую сумму квадратов на p (количество факторов в уравнении регрессии ) для получения оценки объяснённой дисперсии переменной y (S2объясн ), которая характеризует вариацию зависимого показателя, объяснённую построенным уравнением регрессии;
3)остаточную сумму квадратов на (np1) для получения оценки остаточной дисперсии зависимой переменной (S2ост), которая характеризует разброс значений относительно линии регрессии.

Среднеквадратическое отклонение от линии регрессии есть квадратный корень из значения S2ост (чаще называется стандартной ошибкой регрессии S = 
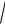 Sост2 ).
Sост2 ).
Величина R2 – множественный коэффициент детерминации, показывает, какая часть дисперсии функции отклика объясняется вариацией линейной комбинации выбранных факторов x1,x2,..,xj,..,xp.
R2=1− Qост = Qобъясн
Qобщ Qобщ
Измеряется в долях единицы (от 0 до 1) либо в процентах (от 0 до
100%).
Квадратный корень из коэффициента детерминации есть коэффициент множественной корреляции, характеризует тесноту связи между функцией отклика и совокупностью факторов, включённых в уравнение.
Проверка значимости уравнения регрессии:
Н0: все βj = 0; Н1: существует хотя бы один βj ≠ 0.
Уравнение регрессии значимо, если |
F p= |
Sобъясн2 |
F ,k |
|
k |
|
, |
где k1 = p, |
|||||||||||||
Sост2 |
1, |
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
k2 = n p 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Проверка значимости параметров: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Н0: βj = 0; Н1: βj ≠ 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Расчётное значение tстатистики Стьюдента t = |
|
bj |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Sb j |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где |
|
bj |
|
|
абсолютное значение оценки параметра β j ; |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||||||
Sbj стандартная ошибка параметра, определяемая по формуле : |
|||||||||||||||||||||
Sbj =S √ |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
[( X T X )−1] jj |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где |
[( X T X )−1] jj |
диагональный элемент |
матрицы, |
обратной |
|||||||||||||||||
матрице нормальных уравнений X T X . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Если |
|
|
t расч t ,n− p−1 |
то данный |
фактор оказывает |
|
существенное |
||||||||||||||
(значимое) влияние на результирующую переменную.
