Непосредственное интегрирование
Метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием. См. Таблица интегралов.
Подведение под знак дифференциала
Данный метод эквивалентен методу замены переменной (см. далее):
Метод замены переменной (метод подстановки)
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть
требуется вычислить интеграл 
Сделаем
подстановку 
где 
—
функция, имеющая непрерывную производную.
Тогда 
и
на основании свойства инвариантности
формулы интегрирования неопределенного
интеграла получаем формулу
интегрирования подстановкой:
\Интегрирование
выражений вида 
Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.
Если n нечётное, n > 0, то удобнее сделать подстановку cos x = t.
Если n и m чётные, то удобнее сделать подстановку tg x = t.
Приложения определенного интеграла.
Приложения определенного интеграла.
1. Вычисление площади криволинейной трапеции.
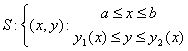
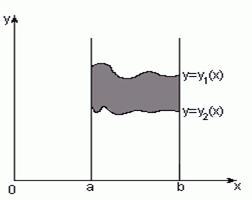
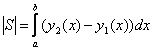
П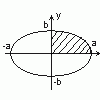
ример. Вычислить площадь ограниченную
эллипсом 
Ввиду очевидной симметрии эллипса относительно осей координат, достаточно вычислить четвёртую часть площади, расположенную в правом верхнем квадранте.
Из
уравнения эллипса находим y как
функцию от x: y(x)=b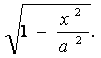
Тогда площадь эллипса вычисляем по формуле:
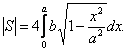Сделав
замену x=asint, 
получим
интеграл: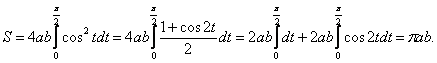 
2. Вычисление объёмов тела, площади сечения которых известны.
-
z
-
x’
-
x
Пусть для некоторого тела в пространстве известно значение S(x) – площади сечения этого тела плоскостью, проходящей через точку x’ и параллельной плоскости OYZ.
Тогда
объём этого тела может быть вычислен
по формуле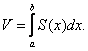 
Пример. Вычислить
объём эллипсоида 
В
сечении эллипсоида плоскостью, проходящей
через точку x, 
параллельной
плоскостью OYZ будет
эллипс: 
или 
Как
было доказано в предыдущем примере,
площадь S(x) этого
эллипса равна 
Следовательно, объём эллипсоида можно вычислить по формуле:
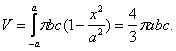
3. Вычисление длинны дуги плоской кривой.
Пусть
кривая Г задана на
плоскости OXY уравнением y=y(x), 
и 
Тогда длинна этой кривой может быть вычислена по формуле:
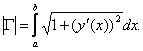
Пример. Вычислить длину окружности x2 + y2 = R2.
В
силу симметрии окружности относительно
осей координат, достаточно длину четверти
окружности, лежащей в первом квадранте.
Выражая из уравнения окружности y как
функцию от x: 
и
подставляя значение 
в
формулу для вычисления длинны дуги
кривой, получим равенство:
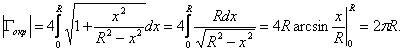
4. Вычисление площади поверхностей вращения плоской кривой вокруг неподвижной оси.
Пусть
кривая Г, заданная как
и выше уравнением y=y(x), 
, 
вращается
вокруг оси OX.
Тогда площадь поверхности вращения
этой кривой может быть вычислена по
формуле:
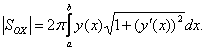
Пример. Вычислить площадь поверхности сферы x2 + y2 + z2 = R2.
Площадь
поверхности сферы можно представить
как площадь поверхности вращения
кривой 
вокруг
оси OX.
Пользуясь формулой для площади поверхности вращения кривой вокруг оси OX, получим значение площади поверхности сферы:
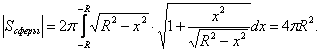
Понятие комплексного числа.
Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:
Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда
a = c и b = d.
Суммой двух комплексных чисел a + ib и c + id называется комплексное число
a + c + i(b + d).
Произведением двух комплексных чисел a + ib и c + id называется комплексное число
|
ac – bd + i(ad + bc). |
Геометрическое изображение комплексных чисел.
Действительные числа можно изобразить точками прямой линии, как показано на рисунке, где точка A изображает число 4, а точка B число -5. Эти же числа можно изображать также отрезками OA, OB, учитывая не только их длину, но и направление.
Каждая точка M числовой прямой изображает некоторое действительное число (рациональное, если отрезок OM соизмерим с единицей длины, и иррациональное если несоизмерим). Таким образом, на числовой прямой не остается места для комплексных чисел.
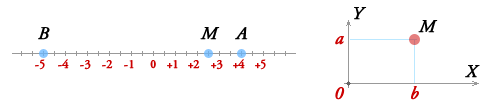
Но комплексные числа можно изображать на числовой плоскости. Для этого мы выбираем на плоскости прямоугольную систему координат, с одинаковым масштабом на обеих осях.
Комплексное число a + b·i изображается точкой M, у которой абсцисса x равна абсциссе a комплексного числа, а ордината y равна ординате bкомплексного числа.
Формы записи комплексных чисел
Сумма и произведение комплексных чисел z1=(x1,y1) и z2=(x2,y2) определяются равенствами
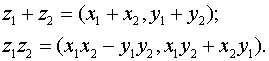
В частности:
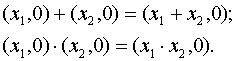
Следовательно,
множество действительных чисел
вкладывается в множество комплексных
чисел и можно отождествить комплексное
число вида (x,0) и действительное число x:
(x,0)
x.
Введем обозначение
.
Тогда по правилам умножения
.
Теперь любое комплексное число можно записать в виде
При этом x называют действительной частью z и обозначают Rez, а y – мнимой частью z и обозначают Imz.
Такую форму записи называют алгебраической формой записи комплексного числа.
Действия над комплексными числами.
алгебраической формой записи комплексного числа. Арифметические операции с комплексными числами в алгебраической форме могут быть записаны следующим образом:
сложение 
вычитание 
умножение 
.
(Как видно из последнего равенства, комплексные числа перемножаются как двучлены.)
Деление:
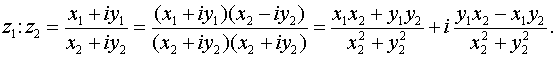
Возведение в степень:
,
где n – целое положительное число.
(Отметим, что перемножать, делить и возводить в степень часто удобнее, когда комплексное число задается в тригонометрической или показательной форме, см. далее по тексту.)
Комплексные
числа 
–
называют сопряженными
Общие сведения о дифференциальных уравнениях.
Дифференциа́льное
уравне́ние — уравнение,
связывающее значение некоторой
неизвестной функции в
некоторой точке и значение
её производных различных
порядков в той же точке. Дифференциальное
уравнение содержит в своей записи
неизвестную функцию, её производные и
независимые переменные; однако не любое
уравнение, содержащее производные
неизвестной функции, является
дифференциальным уравнением. Например, 
не
является дифференциальным уравнением.
Стоит также отметить, что дифференциальное
уравнение может вообще не содержать
неизвестную функцию, некоторые её
производные и свободные переменные, но
обязано содержать хотя бы одну из
производных.
Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него.
Решением
(интегралом)
дифференциального
уравнения порядка n называется функция y(x),
имеющая на некотором интервале (a,
b) производные 
до
порядка n включительно
и удовлетворяющая этому уравнению.
Процесс решения дифференциального
уравнения называется интегрированием.
Вопрос об интегрировании дифференциального
уравнения считается решенным, если
нахождение неизвестной функции удается
привести к квадратуре,
независимо от того, выражается ли
полученный интеграл в конечном виде
или нет.
Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.
Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени.
Дифференциальные уравнения первого порядка.
Уравнение
F(x, y, y ') = 0,
где y = y(x) — неизвестная, непрерывно дифференцируема на (a,b) функция, называется обыкновенным дифференциальным уравнением первого порядка.
Функция y = y(x) называется решением дифференциального уравнения F(x, y, y ') = 0, если она непрерывно дифференцируема на (a,b) и F(x, y(x), y'(x)) ≡ 0 для всех x из (a,b) .
График решения дифференциального уравнения называют интегральной кривой дифференциального уравнения.
Дифференциальное уравнение 1–го порядка имеет бесконечно много решений. Для того чтобы выделить единственное решение, нужно задать дополнительные (начальные) условия.
Задача отыскания решения y = y(x) уравнения F(x, y, y ' ) = 0 , удовлетворяющего условию y(x0) = y0, называется задачей Коши (или начальной задачей).
Условие y(x0) = y0 — начальное условие.
Любое конкретное решение y = y(x) (решение задачи Коши) уравнения 1–го порядка, называется частным решением уравнения.
Общее решение уравнения, записанное в неявной форме Φ(x, y) = C, называется общим интегралом уравнения.
Частное решение уравнения, записанное в неявной форме Φ(x, y) = 0, называется частным интегралом уравнения.
Уравнение 1-го порядка, разрешенное относительно производной, называют уравнением, записанными в нормальной форме:
Уравнения первого порядка часто записывают в дифференциальной форме:
M(x, y)dx + N(x, y)dy = 0.
Решение такого уравнения можно искать как в виде y = y(x) , так и в виде x = x(y) .
Дифференциальные уравнения высших порядков.
Линейное
однородное уравнение третьего порядка
имеет следующий вид:
,
где 
–
константы.
Для данного уравнения тоже
нужно составить характеристическое
уравнение и уравнение и найти его корни.
Характеристическое уравнение, как
многие догадались, выглядит так:
,
и оно в
любом случае имеет ровно
три корня.
Пусть,
например, все корни действительны и
различны: 
,
тогда общее решение запишется следующим
образом:
Если
один корень действительный 
,
а два других – сопряженные комплексные 
,
то общее решение записываем так:
Особый
случай, когда все три корня кратны
(одинаковы). Рассмотрим простейшие
однородное ДУ 3-го порядка с одиноким
папашей: 
.
Характеристическое уравнение 
имеет
три совпавших нулевых корня 
.
Общее решение записываем так:
Если
характеристическое уравнение 
имеет,
например, три кратных корня 
,
то общее решение, соответственно,
такое:
Интегрирование ДУ второго порядка с постоянными коэффициентами.
Линейное
однородное уравнение третьего порядка
имеет следующий вид:
,
где 
–
константы.
Для данного уравнения тоже
нужно составить характеристическое
уравнение и уравнение и найти его корни.
Характеристическое уравнение, как
многие догадались, выглядит так:
,
и оно в
любом случае имеет ровно
три корня.
Пусть,
например, все корни действительны и
различны: 
,
тогда общее решение запишется следующим
образом:
Если
один корень действительный 
,
а два других – сопряженные комплексные 
,
то общее решение записываем так:
Особый
случай, когда все три корня кратны
(одинаковы). Рассмотрим простейшие
однородное ДУ 3-го порядка с одиноким
папашей: 
.
Характеристическое уравнение 
имеет
три совпавших нулевых корня 
.
Общее решение записываем так:
Если
характеристическое уравнение 
имеет,
например, три кратных корня 
,
то общее решение, соответственно,
такое:
Линейные неоднородные ДУ
Линейное неоднородное уравнение данного типа имеет вид:
где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:
Теорема: Общее решение неоднородного уравнения является суммой общего решения y0(x) соответствуюшего однородного уравнения и частного решения y1(x) неоднородного уравнения:
Ниже мы рассмотрим два способа решения неоднородных дифференциальных уравнений.
Метод вариации постоянных
Если общее решение y0 ассоциированного однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных. Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид:
Вместо постоянных C1 и C2 будем рассматривать вспомогательные функции C1(x) и C2(x). Будем искать эти функции такими, чтобы решение
удовлетворяло неоднородному уравнению с правой частью f(x). Неизвестные функции C1(x) и C2(x) определяются из системы двух уравнений:
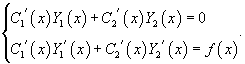
Метод неопределенных коэффициентов
Правая часть f(x) неоднородного дифференциального уравнения часто представляет собой многочлен, экспоненциальную или тригонометрическую функцию, или некоторую комбинацию указанных функций. В этом случае решение удобнее искать с помощью метода неопределенных коэффициентов. Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как
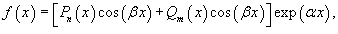где Pn(x) и Qm(x) −
многочлены степени n и m,
соответственно.
В обоих случаях выбор частного решения должен соответствовать структуре правой части неоднородного дифференциального уравнения. В случае 1, если число α в экспоненциальной функции совпадает с корнем характеристического уравнения, то частное решение будет содержать дополнительный множитель xs, где s − кратность корня α в характеристическом уравнении. В случае 2, если число α + βi совпадает с корнем характеристического уравнения, то выражение для частного решения будет содержать дополнительный множитель x. Неизвестные коэффициенты можно определить подстановкой найденного выражения для частного решения в исходное неоднородное дифференциальное уравнение.
Принцип суперпозиции
Если правая часть неоднородного уравнения представляет собой сумму нескольких функций вида
то частное решение дифференциального уравнения также будет являться суммой частных решений, построенных отдельно для каждого слагаемого в правой части.
Составил преподаватель Пасынкова Е.В.