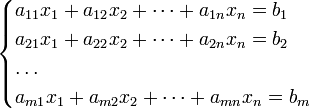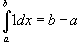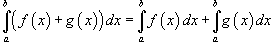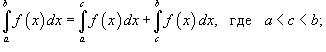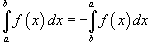|
СОГЛАСОВАНО На заседании методического совета ________________А.А.Григорьева Протокол №__________ «____» ______________2012 г. |
УТВЕРЖДАЮ Зам. директора ТК ТГТУ по УПР ___________Е.Э. Дорошина
«____» _ ____________________2012 г. |
Вопросы к экзамену по учебной дисциплине «Элементы высшей математики»
для специальности 230115 «Программирование в компьютерных системах »
2012\2013уч.год.
Матрицы и действия над ними.
(О. Нулевой матрицей называется матрица все элементы которой равны 0.
О. Две матрицы одинаковой размерности mxn называются равными, если на пересечении i-й строки и j-го столбца в одной и в другой матрице стоит одно и то же число; i=1, 2, ..., m ; j=1, 2, ..., n .
Пусть A = (aij) – некоторая матрица и g–произвольное число,тогда g A = (g aij), то есть при умножении матрицы A на число g все числа, составляющие матрицу A, умножаются на число g.
Пусть A и B – матрицы одинаковой размерности A = (aij), B = (bij), тогда их сумма A + B – матрица C = (cij) той же размерности, определяемая из формулы cij = aij + bij, то есть при сложении двух матриц попарно складываются одинаково расположенные в них числа.
Матрицу A можно умножить на матрицу B, то есть найти матрицу C = AB, если число столбцов n матрицы A равно числу строк матрицы B, при этом матрица C будет иметь столько строк, сколько строк у матрицы A и столько столбцов, сколько столбцов у матрицы B. Каждый элемент матрицы C определяется формулой.
Элемент cij матрицы-произведения C равен сумме произведений элементов i -строки первой матрицы- сомножителя на соответствующие элементы j -го столбца второй матрицы - сомножителя.
Понятие определителя и его свойства.
У этого термина существуют и другие значения, см. Определитель (значения).
Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.
СВОЙСТВО 1. Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером, то есть
СВОЙСТВО 2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на -1.
СВОЙСТВО 3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.
СВОЙСТВО 4. Умножение всех элементов одного столбца или одной строки определителя на любое число k равносильно умножению определителя на это число k.
СВОЙСТВО 5. Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю. Это свойство есть частный случае предыдущего (при k=0).
СВОЙСТВО 6. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.
СВОЙСТВО 7. Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же.
СВОЙСТВО 8. Если к элементам некоторого столбца (или некоторой строки) прибавить соответствующие элементы другого столбца (или другой строки), умноженные на любой общий множитель, то величина определителя при этом не изменится. Например. Дальнейшие свойства определителей связаны с понятием алгебраического дополнения и минора. Минором некоторого элемента называется определитель, получаемый из данного путем вычеркиванием строки и столбца, на пересечении которых расположен этот элемент.
Алгебраическое дополнение любого элемента определителя равняется минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число четное, и с обратным знаком, если это число нечетное.
Алгебраическое дополнение элемента мы будем обозначать большой буквой того же наименования и тем же номером, что и буква, кторой обозначен сам элемент.
СВОЙСТВО 9. Определитель равен сумме произведений элементов какого-либо столбца (или строки) на их алгебраические дополнения. Иначе говоря, имеют место следующие равенства:
Вычисление определителей.
Вычисление определителей основывается на их известных свойствах, которые относятся к определителям всех порядков. Вот эти свойства:
1. Если переставить две строки (или два столбца) определителя, то определитель изменит знак.
2. Если соответствующие элементы двух столбцов (или двух строк) определителя равны или пропорциональны, то определитель равен нулю.
3. Значение определителя не изменится, если поменять местами строки и столбцы, сохранив их порядок.
4. Если все элементы какой-либо строки (или столбца) имеют общий множитель, то его можно вынести за знак определителя.
5. Значение определителя не изменится, если к элементам одной строки (или столбца) прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число. Для определителей третьего порядка это свойство может быть записано, например, так:
![]()
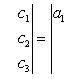
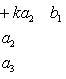
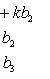
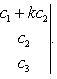
6. Определитель второго порядка вычисляется по формуле
![]()
![]()
![]() (1)
(1)
7. Определитель третьего порядка вычисляется по формуле
![]()
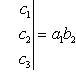
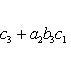
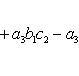
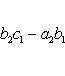
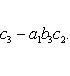 (2)
(2)
Существует удобная схема для вычисления определителя третьего порядка (см. рис. 1 и рис. 2).
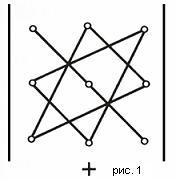
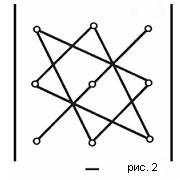
По схеме, приведенной на рис. 1, произведения соединеных элементов берутся со своим знаком, а по схеме рис. 2 - с обратным. Величина определителя равна алгебраической сумме полученных шести произведений.
Системы линейных уравнений. Основные понятия и определения.
Система mр линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида
|
|
(1) |
![]()
Система линейных уравнений от трёх переменных определяет наборплоскостей. Точка пересечения является решением.
Здесь ![]() —
количество уравнений, а
—
количество уравнений, а ![]() —
количество неизвестных. x1, x2,
…, xn —
неизвестные, которые надо определить. a11, a12,
…, amn —
коэффициенты системы — и b1, b2,
… bm —
свободные члены — предполагаются
известными[1].
Индексы коэффициентов (aij)
системы обозначают номера уравнения
(i)
и неизвестного (j),
при котором стоит этот коэффициент,
соответственно[2].
—
количество неизвестных. x1, x2,
…, xn —
неизвестные, которые надо определить. a11, a12,
…, amn —
коэффициенты системы — и b1, b2,
… bm —
свободные члены — предполагаются
известными[1].
Индексы коэффициентов (aij)
системы обозначают номера уравнения
(i)
и неизвестного (j),
при котором стоит этот коэффициент,
соответственно[2].
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы (1) — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения в тождества.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:
|
c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2). |
Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называетсянеопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.
Методы решения систем линейных уравнений (метод Крамера и Гаусса).
Ме́тод Га́усса[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные[2].
Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод.
Векторы. Линейные операции над ними.
Вектором называется направленный отрезок. Если начало вектора находится в точке А, а конец – в точке В, то вектор обозначается АВ. Если же начало и конец вектора не указываются, то его обозначают строчной буквой латинского алфавита a, b, c ,…. Через BA обозначают вектор, направленный противоположно вектору АВ. Вектор, у которого начало и конец совпадают, называется нулевым и обозначается ō. Его направление является неопределенным.
Длиной или модулем вектора называется расстояние между его началом и концом. Записи |АВ| и |a| обозначают модули векторов АВ и a.
Векторы называются коллинеарными, если они параллельны одной прямой, и компланарными, если они параллельны одной плоскости.
Два вектора называются равными, если они коллинеарны, одинаково направлены и равны по длине.
К линейным операциям над векторами относятся:
1) умножение вектора на число (Произведением вектора a и числа α называется вектор, обозначаемый α∙a. (или наоборот a∙α), модуль которого равен |α a| =|α||a|, а направление совпадает с направлением вектора a, если α>0, и противоположно ему, если α< 0.
2)
сложение векторов (Суммой векторов ![]() называется
вектор, обозначаемый
называется
вектор, обозначаемый ![]() ,
начало которого находится в начале
первого вектора a1,
а конец – в конце последнего вектора
an,
ломаной линии, составленной из
последовательности слагаемых векторов.
Это правило сложения называется правилом
замыкания ломаной. В случае суммы двух
векторов оно равносильно правилу
параллелограмма)
,
начало которого находится в начале
первого вектора a1,
а конец – в конце последнего вектора
an,
ломаной линии, составленной из
последовательности слагаемых векторов.
Это правило сложения называется правилом
замыкания ломаной. В случае суммы двух
векторов оно равносильно правилу
параллелограмма)
Прямая е с заданным на ней направлением, принимаемым за положительное, называется осью е.
Линейной
комбинацией векторов ai называется
вектор a, определяемый по формуле ![]() ,
где
,
где ![]() –
некоторые числа.
–
некоторые числа.
Если для системы n векторов ai равенство
![]()
верно
только в случае, когда ![]() эта
система называется линейно независимой.
Если же равенство (1) выполняется для
эта
система называется линейно независимой.
Если же равенство (1) выполняется для ![]() ,
хотя бы одно из которых отлично от нуля,
то система векторов aі называется линейно
зависимой. Например, любые коллинеарные
векторы, три компланарных вектора,
четыре и более векторов в трехмерном
пространстве всегда линейно зависимы.
,
хотя бы одно из которых отлично от нуля,
то система векторов aі называется линейно
зависимой. Например, любые коллинеарные
векторы, три компланарных вектора,
четыре и более векторов в трехмерном
пространстве всегда линейно зависимы.
Три упорядочных линейно независимых вектора ē1, ē2, ē3 в пространстве называется базисом. Упорядоченная тройка некомпланарных векторов всегда образует базис. Любой вектор a в пространстве можно разложить по базису ē1, ē2, ē3, т. е. представить a в виде линейной комбинации базисных векторов: a= xē1 + yē2 + zē3, где x, y, z являются координатами вектора a в базисе ē1, ē2, ē3. Базис называется ортонормированным, если его векторы взаимно перпендикулярны и имеют единичную длину. Обозначают такой базис i, j, k, т. е. i=(1, 0, 0), j=(0, 1, 0), k=(0, 0, 1).
Пример
5. Векторы заданы в ортонормированном
базисе i, j, k координатами: a=(2;-1;8), е1 =
(1,2,3), е2 =
(1,-1,-2), е3 =
(1,-6,0). Убедиться, что тройка е1,е2,е3 образует
базис, и найти координаты вектора![]() в
этом базисе.
в
этом базисе.
Решение.
Если определитель 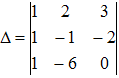 ,
составленный из координат векторов е1,
е2,
е3,
не равен 0, то векторы е1,е2,е3 линейно
независимы и, следовательно, образуют
базис. Убеждаемся, что
,
составленный из координат векторов е1,
е2,
е3,
не равен 0, то векторы е1,е2,е3 линейно
независимы и, следовательно, образуют
базис. Убеждаемся, что ![]() =
-18-4+3-12=-31 Таким образом, тройка е1,
е2,
е3 -
базис.
=
-18-4+3-12=-31 Таким образом, тройка е1,
е2,
е3 -
базис.
Обозначим координаты вектора a в базисе е1, е2, е3 через x,y,z. Тогда а = (x,y,z) = хе1 + yе2 + zе3. Так как по условию а = 2i – j +8k , е1 = i +2j +3k , е2 = i – j -2k, е3 = i – 6j , то из равенства а = хе1 + yе2 + zе3следует, что 2i – j +8k = xi + 2xj + 3xk + yi – yj -2yk +zi -6zj = (x+y+z)i +(2x-y-6z)j +(3x-2y)k..Как видно, вектор в левой части полученного равенства равен вектору в правой его части, а это возможно только в случае равенства их соответствующих координат. Отсюда получаем систему для нахождения неизвестных x, y, z:
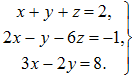
Ее решение: x = 2, y = -1, z = 1. Итак, а = 2е1 – е2 + е3 = (2,-1,1).
Разложение векторов. Скалярное произведение векторов.
Скаля́рное произведе́ние иногда внутреннее произведение — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины вектора x на проекцию вектора y на вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.
Обычно используется одно из следующих обозначений:
![]() ,
,
![]() ,
,
![]() ,
,
или (обозначение Дирака, часто применяемое в квантовой механике для векторов состояния):
![]() .
.
Обычно предполагается, что скалярное произведение положительно определено, то есть
![]() для
всех
для
всех ![]() .
.
Если этого не предполагать, то произведение называется индефинитным.
Скалярным
произведением в векторном
пространстве ![]() над полем
над полем ![]() комплексных (или
комплексных (или ![]() вещественных) чисел называется
функция
вещественных) чисел называется
функция ![]() для
элементов
для
элементов ![]() ,
принимающая значения в
,
принимающая значения в ![]() (или
(или ![]() ),
определенная для каждой пары элементов
и удовлетворяющая следующим условиям:
),
определенная для каждой пары элементов
и удовлетворяющая следующим условиям:
для любых трех элементов
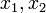 и
и 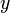 пространства
пространства  и
любых чисел
и
любых чисел 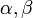 из
из 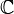 (или
(или 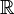 )
справедливо равенство
)
справедливо равенство 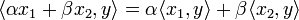 (линейность
скалярного произведения по первому
аргументу);
(линейность
скалярного произведения по первому
аргументу);для любых
 и
и 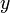 справедливо
равенство
справедливо
равенство 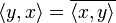 ,
где черта означает комплексное сопряжение
(эрмитова симметричность);
,
где черта означает комплексное сопряжение
(эрмитова симметричность);для любого
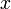 имеем
имеем 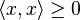 ,
причем
,
причем 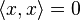 только
при
только
при 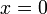 (положительная
определенность скалярного произведения).
(положительная
определенность скалярного произведения).
Заметим,
что из п.2 определения следует, что ![]() .
Поэтому п.3 имеет смысл, несмотря на
комплексные (в общем случае)
значения скалярного
произведения.
.
Поэтому п.3 имеет смысл, несмотря на
комплексные (в общем случае)
значения скалярного
произведения.
Векторное произведение векторов.
Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Произведение не является ни коммутативным, ни ассоциативным (оно является антикоммутативным) и отличается от скалярного произведения векторов. Во многих задачах инженерии и физики нужно иметь возможность строить вектор, перпендикулярный двум имеющимся — векторное произведение предоставляет эту возможность. Векторное произведение полезно для «измерения» перпендикулярности векторов — длина векторного произведения двух векторов равна произведению их длин, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны либо антипараллельны.
Определить векторное произведение можно по-разному, и теоретически, в пространстве любой размерности n можно вычислить произведение n-1 векторов, получив при этом единственный вектор, перпендикулярный к ним всем. Но если произведение ограничить нетривиальными бинарными произведениями с векторным результатами, то традиционное векторное произведение определено только в трёхмерном и семимерном пространствах. Результат векторного произведения, как и скалярного, зависит от метрики Евклидова пространства.
В отличие от формулы для вычисления по координатам векторов скалярного произведения в трёхмерной прямоугольной системе координат, формула для векторного произведения зависит от ориентации прямоугольной системы координат или, иначе, её «хиральности».
Смешанное произведение векторов
Сме́шанное
произведе́ние ![]() векторов
векторов ![]() — скалярное
произведение вектора
— скалярное
произведение вектора ![]() на векторное
произведение векторов
на векторное
произведение векторов ![]() и
и ![]() :
:
![]() .
.
Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрический
смысл: Модуль
смешанного произведения численно равен
объёму параллелепипеда,
образованного векторами ![]() .
.
Смешанное произведение кососимметрично по отношению ко всем своим аргументам:
![]()
т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что
![]()
Смешанное произведение
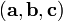 в
правой декартовой системе координат
(в ортонормированном базисе)
равно определителю матрицы,
составленной из векторов
в
правой декартовой системе координат
(в ортонормированном базисе)
равно определителю матрицы,
составленной из векторов 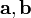 и
и 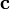 :
:
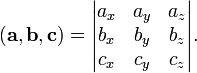
Смешанное произведение
 в
левой декартовой системе координат (в
ортонормированном базисе)
равно определителю матрицы,
составленной из векторов
в
левой декартовой системе координат (в
ортонормированном базисе)
равно определителю матрицы,
составленной из векторов  и
и  ,
взятому со знаком «минус»:
,
взятому со знаком «минус»:
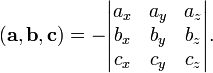
В частности,
Если какие-то два вектора коллинеарны, то с любым третьим вектором они образуют смешанное произведение, равное нулю.
Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю.
Геометрический смысл — Смешанное произведение
 по
абсолютному значению равно
объёму параллелепипеда (см.
рисунок), образованного векторами
по
абсолютному значению равно
объёму параллелепипеда (см.
рисунок), образованного векторами  и
и  ;
знак зависит от того, является ли эта
тройка векторов правой или левой.
;
знак зависит от того, является ли эта
тройка векторов правой или левой.Квадрат смешанного произведения векторов равен определителю Грама, определяемому ими[1]:215.
Смешанное произведение удобно записывается с помощью символа (тензора) Леви-Чивита:
![]()
(в последней формуле в ортонормированном базисе все индексы можно писать нижними; в этом случае эта формула совершенно прямо повторяет формулу с определителем, правда, при этом автоматически получается множитель (-1) для левых базисов).
Декартова прямоугольная система координат на плоскости.
Возьмем на плоскости две взаимно перпендикулярные прямые – две оси координат Ох и Оу с указанными на них положительными направлениями (рис.1). Прямые Ох и Оу называются координатными осями, точка их пересечения О – началом координат.
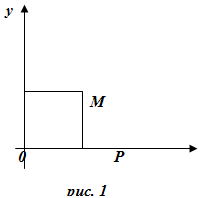
Координатные оси Ох, Оу с выбранной единицей масштаба называются декартовой прямоугольной (или прямоугольной) системой координат на плоскости.
Произвольной точке М плоскости поставим в соответствие два числа: абсциссу х, равную расстоянию от точки М до оси Оу, взятому со знаком «+», если М лежит правее Оу, и со знаком «-» ,если М лежит левее Оу; ординату у, равную расстоянию от точки М до оси Ох, взятому со знаком «+», если М лежит выше Ох, и со знаком «-», если М лежит ниже Ох. Абсцисса х и ордината у называются декартовыми прямоугольными координатами точки М(х;у).
Начало координат имеет координаты (0;0). Оси координат делят плоскость на четыре части, называемые четвертями или квадрантами (иногда их также называют координатными углами). Часть плоскости, заключенная между положительными полуосями Oх и Oу, называется первым квадрантом. Дальше нумерация квадрантов идет против часовой стрелки (рис. 2). Для всех точек I квадранта х>0, у>0; для точек I I квадранта х<0, у>0, в I I I квадранте х<0, у<0 и в IV квадранте х>0, у<0.
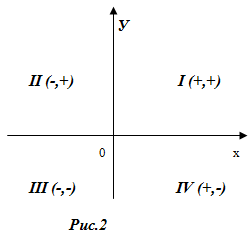
Полярные координаты.
Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.
Полярная
система координат задаётся лучом,
который называют нулевым или полярной
осью. Точка, из которой выходит этот
луч, называется началом координат или
полюсом. Любая точка на плоскости
определяется двумя полярными координатами:
радиальной и угловой. Радиальная
координата (обычно обозначается ![]() )
соответствует расстоянию от точки до
начала координат. Угловая координата,
также называется полярным углом
или азимутом и
обозначается
)
соответствует расстоянию от точки до
начала координат. Угловая координата,
также называется полярным углом
или азимутом и
обозначается ![]() ,
равна углу, на который нужно повернуть
против часовой стрелки полярную ось
для того, чтобы попасть в эту точку.[1]
,
равна углу, на который нужно повернуть
против часовой стрелки полярную ось
для того, чтобы попасть в эту точку.[1]
Определённая таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за предел
Уравнение прямой на плоскости
|
|
Ах + Ву + С = 0,
причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат
• А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох
• В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу
• В = С = 0, А ≠0 – прямая совпадает с осью Оу
• А = С = 0, В ≠0 – прямая совпадает с осью Ох
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
Основные задачи использования уравнения прямой
Не могу ответить
Кривые второго порядка
Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
![]()
в
котором по крайней мере один из
коэффициентов ![]() отличен
от нуля.
отличен
от нуля.
Предел числовой последовательности и функции
Предел числовой последовательности. Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу a приувеличении порядкового номера n. В этом случае говорят, что числовая последовательность имеет предел. Это понятие имеет более строгоеопределение.
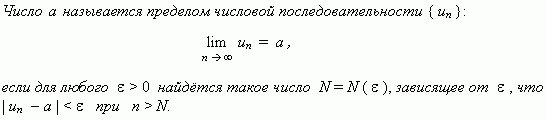
Это
определение означает, что a
есть предел числовой
последовательности, если её общий член
неограниченно приближается к a
при возрастании n.
Геометрически это значит, что для
любого ![]() >
0 можно
найти такое число N,
что начиная с n > N
все члены
последовательности расположены внутри
интервала ( a
>
0 можно
найти такое число N,
что начиная с n > N
все члены
последовательности расположены внутри
интервала ( a ![]() a
a ![]() ).
Последовательность, имеющая предел,
называется сходящейся;
в противном случае – расходящейся.
).
Последовательность, имеющая предел,
называется сходящейся;
в противном случае – расходящейся.
Последовательность
называется ограниченной,
если существует такое число M,
что | un
| ![]() Mдля
всех n . Возрастающая
или убывающая последовательность
называется монотонной.
Mдля
всех n . Возрастающая
или убывающая последовательность
называется монотонной.
Основные теоремы о пределах и их применение
Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.
![]()
![]()
![]() .
.
Теорема 2. (о предельном переходе в неравенстве) Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x) , то предел функции f(x) в этой точке не превосходит предела функции g(x).
![]()
![]()
![]() .
.
Теорема 3. Предел постоянной равен самой постоянной.
![]() .
.
Доказательство. f(x)=с, докажем,
что ![]() .
.
Возьмем произвольное >0. В качестве можно взять любое
положительное
число. Тогда при ![]()
![]() .
.
Теорема 4. Функция не может иметь двух различных пределов в
одной точке.
Доказательство. Предположим противное. Пусть
![]() и
и ![]() .
.
По теореме о связи предела и бесконечно малой функции:
f(x)-A=![]() -
б.м. при
-
б.м. при ![]() ,
,
f(x)-B=![]() -
б.м. при
-
б.м. при ![]() .
.
Вычитая
эти равенства, получим:![]()
B-A=![]() -
-![]() .
.
Переходя
к пределам в обеих частях равенства при ![]() ,
имеем:
,
имеем:
B-A=0, т.е. B=A. Получаем противоречие, доказывающее теорему.
Теорема
5. Если
каждое слагаемое алгебраической суммы
функций имеет предел при ![]() ,
то и алгебраическая сумма имеет предел
при
,
то и алгебраическая сумма имеет предел
при ![]() ,
причем предел алгебраической суммы
равен алгебраической сумме пределов.
,
причем предел алгебраической суммы
равен алгебраической сумме пределов.
![]()
![]()
![]()
![]() .
.
Доказательство. Пусть ![]() ,
, ![]() ,
, ![]() .
.
Тогда, по теореме о связи предела и б.м. функции:
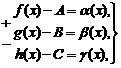 где
где ![]() -
б.м.
при
-
б.м.
при![]() .
.
Сложим алгебраически эти равенства:
f(x)+g(x)-h(x)-(А+В-С)=![]() ,
,
где ![]() б.м.
при
б.м.
при ![]() .
.
По теореме о связи предела и б.м. функции:
![]() А+В-С=
А+В-С=![]()
![]()
![]() .
.
Теорема 6. Если
каждый из сомножителей произведения
конечного числа функций имеет предел при ![]() ,
то и произведение имеет предел при
,
то и произведение имеет предел при![]() ,
причем предел произведения равен
произведению пределов.
,
причем предел произведения равен
произведению пределов.
![]()
![]()
![]() .
.
Следствие. Постоянный множитель можно выносить за знак предела.
![]()
![]()
![]() .
.
Теорема 7. Если
функции f(x) и g(x) имеют
предел при ![]() ,
,
причем ![]() ,
то и их частное имеет предел при
,
то и их частное имеет предел при ![]() ,
причем предел частного равен частному
пределов.
,
причем предел частного равен частному
пределов.
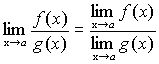 ,
, ![]() .
.
Непрерывность функции
На
рис. 15, а изображен график функции ![]() .
Его естественно назвать непрерывным
графиком, потому что он может быть
нарисован одним движением карандаша
без отрыва от бумаги. Зададим произвольную
точку (число)
.
Его естественно назвать непрерывным
графиком, потому что он может быть
нарисован одним движением карандаша
без отрыва от бумаги. Зададим произвольную
точку (число) ![]() .
Близкая к ней другая точка
.
Близкая к ней другая точка ![]() может
быть записана в виде
может
быть записана в виде ![]() ,
где
,
где ![]() есть
число положительное или отрицательное,
называемое приращением
есть
число положительное или отрицательное,
называемое приращением ![]() .
Разность
.
Разность
![]()
называется
приращением функции ![]() в
точке
в
точке ![]() ,
соответствующим приращению
,
соответствующим приращению ![]() .
Здесь имеется в виду
.
Здесь имеется в виду ![]() такое,
что
такое,
что ![]() .
На рис. 15, а
.
На рис. 15, а ![]() равно
длине отрезка
равно
длине отрезка ![]() .
.
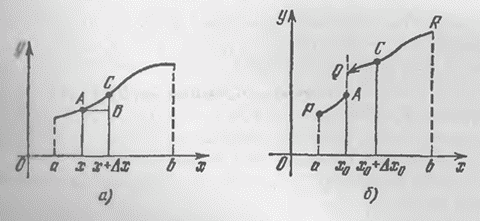
Рис. 15
Будем
стремить ![]() к
нулю; тогда для рассматриваемой функции,
очевидно, и
к
нулю; тогда для рассматриваемой функции,
очевидно, и ![]() будет
стремиться к нулю:
будет
стремиться к нулю:
![]() .
(1)
.
(1)
Рассмотрим
теперь график на рис 15, б. Он состоит из
двух непрерывных кусков ![]() и
и ![]() .
Однако эти куски не соединены непрерывно,
и потому график естественно назвать
разрывным. Чтобы график изображал
однозначную функцию
.
Однако эти куски не соединены непрерывно,
и потому график естественно назвать
разрывным. Чтобы график изображал
однозначную функцию ![]() в
точке
в
точке ![]() ,
условимся, что
,
условимся, что ![]() равно
длине отрезка, соединяющего
равно
длине отрезка, соединяющего ![]() и
и ![]() ;
в знак этого точка
;
в знак этого точка ![]() изображена
на графике кружком, в то время как у
точки
изображена
на графике кружком, в то время как у
точки ![]() нарисована
стрелка, указывающая, что
нарисована
стрелка, указывающая, что ![]() не
принадлежит графику. Если бы
точка
не
принадлежит графику. Если бы
точка ![]() принадлежала
графику, то функция
принадлежала
графику, то функция ![]() была
бы двузначной в точке
была
бы двузначной в точке ![]() .
.
Придадим
теперь ![]() приращение
приращение ![]() и
определим соответствующее приращение
функции:
и
определим соответствующее приращение
функции:
![]() .
.
Если
мы будем ![]() стремить
к нулю, то теперь уже нельзя сказать,
что
стремить
к нулю, то теперь уже нельзя сказать,
что ![]() будет
стремиться к нулю. Для отрицательных
будет
стремиться к нулю. Для отрицательных ![]() ,
стремящихся к нулю, это так, но для
положительных вовсе не так: из рисунка
видно, что если
,
стремящихся к нулю, это так, но для
положительных вовсе не так: из рисунка
видно, что если ![]() ,
оставаясь положительным, стремится к
нулю, то соответствующее приращение
,
оставаясь положительным, стремится к
нулю, то соответствующее приращение ![]() при
этом стремится к положительному числу,
равному длине отрезка
при
этом стремится к положительному числу,
равному длине отрезка![]() .
.
После
этих рассмотрений естественно функцию ![]() ,
заданную на отрезке
,
заданную на отрезке ![]() ,
называть непрерывной в точке
,
называть непрерывной в точке ![]() этого
отрезка, если приращение ее в этой точке,
соответствующее приращению
этого
отрезка, если приращение ее в этой точке,
соответствующее приращению ![]() ,
стремится к нулю при любом способе
стремления
,
стремится к нулю при любом способе
стремления ![]() к
нулю. Это (свойство непрерывности
к
нулю. Это (свойство непрерывности ![]() в
в ![]() )
записывается в виде соотношения (1) или
еще так:
)
записывается в виде соотношения (1) или
еще так:
![]() .
(2)
.
(2)
Запись
(2) читается так: предел ![]() равен
нулю, когда
равен
нулю, когда ![]() стремится
к нулю по любому закону. Впрочем, выражение
«по любому закону» обычно опускают,
подразумевая его.
стремится
к нулю по любому закону. Впрочем, выражение
«по любому закону» обычно опускают,
подразумевая его.
Если
определенная на ![]() функция
функция ![]() не
является непрерывной в точке
не
является непрерывной в точке ![]() ,
т. е. если для нее не выполняется свойство
(2) хотя бы при одном способе стремления
,
т. е. если для нее не выполняется свойство
(2) хотя бы при одном способе стремления ![]() к
нулю, то она называется разрывной в
точке
к
нулю, то она называется разрывной в
точке ![]() .
.
Функция,
изображенная на рис. 15, а, непрерывна в
любой точке ![]() ,
функция же, изображенная на рис. 15, б,
очевидно, непрерывна в любой точке
,
функция же, изображенная на рис. 15, б,
очевидно, непрерывна в любой точке ![]() ,
за исключением точки
,
за исключением точки ![]() ,
потому что для последней соотношение
(2) не выполняется, когда
,
потому что для последней соотношение
(2) не выполняется, когда ![]() ,
оставаясь положительным.
,
оставаясь положительным.
Функция, непрерывная в любой точке отрезка (интервала), называется непрерывной на этом отрезке (интервале).
Непрерывная
функция математически выражает свойство,
с которым нам приходится часто встречаться
на практике, заключающееся в том, что
малому приращению независимой переменной
соответствует малое же приращение
зависимой от нее переменной (функции).
Прекрасными примерами непрерывной
функции могут служить различные законы
движения тел ![]() ,
выражающие зависимости пути
,
выражающие зависимости пути ![]() ,
пройденного телом, от времени
,
пройденного телом, от времени ![]() .
Время и пространство непрерывны. Тот
или иной закон движения
.
Время и пространство непрерывны. Тот
или иной закон движения ![]() устанавливает
между ними определенную непрерывную
связь, характеризующуюся тем, что малому
приращению времени соответствует малое
приращение пути.
устанавливает
между ними определенную непрерывную
связь, характеризующуюся тем, что малому
приращению времени соответствует малое
приращение пути.
К абстракции непрерывности человек пришел, наблюдая окружающие его, так называемые, сплошные среды – твердые, жидкие или газообразные, например металлы, воду, воздух. На самом деле, всякая физическая среда представляет собой скопление большого числа отделенных друг от друга движущихся частиц. Однако эти частицы и расстояния между ними настолько малы по сравнению с объемами сред, с которыми приходится иметь дело в макроскопических физических явлениях, что многие такие явления можно достаточно хорошо изучать, если считать приближенно массу изучаемой среды непрерывно распределенной без всяких просветов в занятом ею пространстве. На таком допущении базируются многие физические дисциплины, например гидродинамика, аэродинамика, теория упругости. Математическое понятие непрерывности, естественно, играет в этих дисциплинах, как и во многих других, большую роль.
Непрерывные функции образуют основной класс функций, с которыми оперирует математический анализ.
Примерами
непрерывных функций могут служить
элементарные функции (см. ниже § 3.8). Они
непрерывны на интервалах изменения ![]() ,
где они определены.
,
где они определены.
Разрывные
функции в математике отражают
скачкообразные процессы, встречающиеся
в природе. При ударе, например, величина
скорости тела меняется скачкообразно.
Многие качественные переходы
сопровождаются скачками. Например,
зависимость ![]() между
температурой одного грамма воды (льда)
и количеством
между
температурой одного грамма воды (льда)
и количеством ![]() калорий
находящегося в ней тепла, когда
калорий
находящегося в ней тепла, когда ![]() изменяется
между
изменяется
между ![]() и
и ![]() ,
если принять условно, что при
,
если принять условно, что при ![]() величина
величина ![]() ,
выражается следующими формулами:
,
выражается следующими формулами:
![]()
Мы
считаем, что теплоемкость льда равна
0,5. При ![]() эта
функция оказывается неопределенной –
многозначной; можно для удобства
условиться, что при
эта
функция оказывается неопределенной –
многозначной; можно для удобства
условиться, что при ![]() она
принимает вполне определенное значение,
например
она
принимает вполне определенное значение,
например ![]() .
Функция
.
Функция ![]() ,
очевидно, разрывная при
,
очевидно, разрывная при ![]() ,
изображена на рис. 16.
,
изображена на рис. 16.
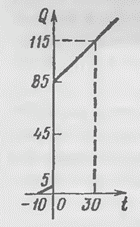
Рис. 16
Дадим
определение непрерывности функции ![]() в
точке.
в
точке.
Функция ![]() называется
непрерывной в точке
называется
непрерывной в точке ![]() ,
если она определена в некоторой
окрестности этой точки, в том числе в
самой точке
,
если она определена в некоторой
окрестности этой точки, в том числе в
самой точке ![]() ,
и если ее приращение в этой точке,
соответствующее приращению аргумента
,
и если ее приращение в этой точке,
соответствующее приращению аргумента ![]() ,
стремится к нулю при
,
стремится к нулю при ![]() :
:
![]() .
(3)
.
(3)
Если
положить ![]() ,
то получим следующее эквивалентное
определение непрерывности
,
то получим следующее эквивалентное
определение непрерывности ![]() в
в ![]() :
функция
:
функция ![]() непрерывна
в точке
непрерывна
в точке ![]() ,
если она определена в некоторой
окрестности этой точки, в том числе в
самой точке
,
если она определена в некоторой
окрестности этой точки, в том числе в
самой точке ![]() ,
и если
,
и если
![]() ;
(4)
;
(4)
или
еще на языке ![]() ,
, ![]() :
если для всякого
:
если для всякого ![]() найдется
найдется ![]() такое,
что
такое,
что
![]() .
.
Равенство (4) можно еще записать следующим образом:
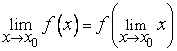 .
(4’)
.
(4’)
Оно показывает, что под знаком непрерывной функции можно переходить к пределу.
П р и
м е р 1. Постоянная ![]() есть
функция, непрерывная в любой точке
есть
функция, непрерывная в любой точке ![]() .
В самом деле, точке
.
В самом деле, точке ![]() соответствует
значение функции
соответствует
значение функции![]() ,
точке
,
точке ![]() соответствует
то же значение
соответствует
то же значение ![]() .
Поэтому
.
Поэтому ![]() и
и
![]() .
.
П р и
м е р 2. Функция ![]() непрерывна
для любого значения
непрерывна
для любого значения ![]() ,
потому что
,
потому что ![]() и,
следовательно,
и,
следовательно, ![]() при
при ![]() .
.
П р и
м е р 3. Функция ![]() непрерывна
для любого
непрерывна
для любого ![]() .
В самом деле,
.
В самом деле,
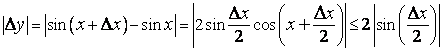 .
(5)
.
(5)
Но для
любого ![]() имеет
место неравенство
имеет
место неравенство
![]() (6)
(6)
Если ![]() ,
то это следует из рис. 17, где изображена
окружность радиуса 1 (дуга длины
,
то это следует из рис. 17, где изображена
окружность радиуса 1 (дуга длины ![]() больше
стягиваемой ею хорды, имеющей длину
больше
стягиваемой ею хорды, имеющей длину ![]() ).
При
).
При ![]() неравенство
(6) обращается в равенство. Если же
неравенство
(6) обращается в равенство. Если же ![]() ,
то
,
то ![]() .
Наконец, если
.
Наконец, если ![]() ,
то
,
то ![]() .
Из (5) на основании (6) следует
.
Из (5) на основании (6) следует
![]() ,
,
т. е.
![]() .
.
Но тогда, очевидно,
![]() .
.
Можно
еще сказать, что для всякого ![]() можно
найти
можно
найти ![]() ,
именно
,
именно ![]() такое,
что
такое,
что
![]() .
.
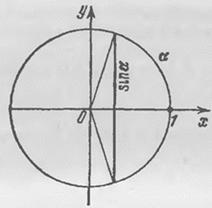
Рис. 17.
Отметим важную теорему.
Т е о
р е м а 1. Если функции ![]() и
и ![]() непрерывны
в точке
непрерывны
в точке ![]() ,
то непрерывны также в этой точке их
сумма, разность, произведение и частное
(при
,
то непрерывны также в этой точке их
сумма, разность, произведение и частное
(при ![]() ).
).
Эта теорема непосредственно вытекает из теоремы 6 §3.2, если учесть, что в данном случае
![]() .
.
Справедлива также важная теорема о непрерывности функции от функции (сложной функции).
Т е о
р е м а 2. Пусть задана функция ![]() ,
непрерывная в точке
,
непрерывная в точке ![]() ,
и еще другая функция
,
и еще другая функция ![]() ,
непрерывная в точке
,
непрерывная в точке ![]() ,
и пусть
,
и пусть ![]() .
Тогда сложная функция
.
Тогда сложная функция ![]() непрерывна
в точке
непрерывна
в точке ![]() .
.
Д о к
а з а т е л ь с т в о. Заметим, что по
определению непрерывности функции ![]() в
точке
в
точке ![]() следует,
что она определена в некоторой окрестности
этой точки. Поэтому
следует,
что она определена в некоторой окрестности
этой точки. Поэтому
![]() .
.
Здесь
введена подстановка ![]() и
учтена непрерывность
и
учтена непрерывность ![]() в
точке
в
точке ![]() .
.
П р и м е р 4. Функция
![]() ,
,
где ![]() -
постоянные коэффициенты, называется
многочленом степени
-
постоянные коэффициенты, называется
многочленом степени ![]() .
Она непрерывна для любого
.
Она непрерывна для любого ![]() .
Ведь чтобы получить
.
Ведь чтобы получить ![]() ,
надо, исходя из постоянных чисел
,
надо, исходя из постоянных чисел ![]() и
функции
и
функции ![]() ,
произвести конечное число арифметических
действий - сложения, вычитания и
умножения. Но постоянная есть непрерывная
функция (см. пример 1), а функция
,
произвести конечное число арифметических
действий - сложения, вычитания и
умножения. Но постоянная есть непрерывная
функция (см. пример 1), а функция ![]() тоже
непрерывна (см. пример 2), поэтому
непрерывность
тоже
непрерывна (см. пример 2), поэтому
непрерывность ![]() следует
из теоремы 1.
следует
из теоремы 1.
П р и
м е р 5. Функция ![]() непрерывна.
Она является композицией двух непрерывных
функций:
непрерывна.
Она является композицией двух непрерывных
функций: ![]() ,
, ![]() .
.
П р и м е р 6. Функция
![]() ,
,
непрерывна
для указанных ![]() ,
потому что (см. теорему 1) она равна
частному от деления непрерывных функций
и при этом делитель не равен нулю (при
указанных
,
потому что (см. теорему 1) она равна
частному от деления непрерывных функций
и при этом делитель не равен нулю (при
указанных ![]() ).
).
П р и м е р 7. Функция
![]()
непрерывна
для любого ![]() ,
потому что она является композицией
непрерывных функций:
,
потому что она является композицией
непрерывных функций: ![]() ,
, ![]() ,
, ![]() (см.
теорему. 2).
(см.
теорему. 2).
П р и
м е р 8. Функция ![]() непрерывна
непрерывна![]() ,
потому что
,
потому что
![]() при
при ![]() .
.
П р и
м е р 9. Если функция ![]() непрерывна
в точке
непрерывна
в точке![]() ,
то непрерывна также в этой точке и
функция
,
то непрерывна также в этой точке и
функция ![]() .
.
Это
следует из теоремы 2 и примера 8,
потому что функция ![]() есть
композиция двух непрерывных функций
есть
композиция двух непрерывных функций![]() ,
, ![]() .
.
Отметим еще две теоремы, которые непосредственно следуют из соответствующих теорем 1 и 2 §3.2 для предела функции.
Т е о
р е м а 3. Если функция ![]() непрерывна
в точке
непрерывна
в точке ![]() ,
то существует окрестность
,
то существует окрестность ![]() этой
точки, на которой
этой
точки, на которой ![]() ограничена.
ограничена.
Т е о
р е м а 4. Если функция ![]() непрерывна
в точке
непрерывна
в точке ![]() и
и ![]() ,
то существует окрестность
,
то существует окрестность ![]() точки
точки ![]() ,
на которой
,
на которой
![]() .
.
Больше
того, если ![]() ,
то
,
то
![]() ,
,
а
если ![]() ,
то
,
то
![]() .
.
Понятие производной.
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.
Геометрический и механический смысл производной..
Не знаю
Правила дифференцирования.
Производная алгебраической суммы функций
выражается следующей теоремой.
Теорема 1. Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:
(u±v)' = u'±v'
Следствие. Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например,
(u — v + w)' = u' — v' + w'
Производную произведения функций определяет
Теорема 2. Производная произведения двух дифференцируемых функций равна произведению первой функции на производную второй плюс произведение второй функции на производную первой, т. е.
(uv)' = u'v + uv'
Следствие 1. Постоянный множитель можно выносить за знак производной (cv)' = cv' (с = const).
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждой из них на все остальные.
Например, (uvw)' = u'vw + uv'w + uvw'
Производная частного двух функций
выражается следующей теоремой.
Теорема 3. Производная частного двух дифференцируемых функций определяется формулой
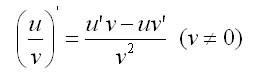
Производную сложной функции выражает
Теорема 4. Если y = f(u) и и = (ф(х)) — дифференцируемые функции своих аргументов, то производная сложной функции у = f (ф(х)) существует и равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т. е.

Очень часто в контрольных по математике на производные даются сложные функции, например, y = sin(cos5x). Производная такой функции равна -5sin5x*sin(cos5x)
Смотрите пример вычисления сложной функции на следующем видео
Производные элементарных функций.
|
Производные элементарных функций простого аргумента |
Функция y = f(kx +b) |
Производные элементарных функций сложного аргумента |
| |
|
y=xn |
y |
y=(kx+b)n |
y | |
|
y = x |
y |
y=(kx+b) |
y | |
|
y= |
y |
y= |
y | |
|
y=x1 |
y |
y=1kx+b |
y | |
|
y = cos x |
y |
y = cos (kx +b) |
y | |
|
y = sin x |
y |
y = sin (kx +b) |
y | |
|
y = tg x |
y |
y = tg (kx +b) |
y | |
|
y = ctg x |
y |
y = ctg (kx +b) |
y | |
|
y = arcsin x |
y |
y = arcsin (kx +b) |
y | |
|
y = arccos x |
y |
y = arccos (kx +b) |
y | |
|
y = arctg x |
y |
y = arctg (kx +b) |
y | |
|
y = arcctg x |
y |
y = arcctg (kx +b) |
y | |
|
y=ax |
y |
y=akx+b |
y | |
|
y=ex |
y |
y=ekx+b |
y | |
|
y=logax |
y |
y=loga(kx+b) |
y | |
|
y = lnx |
y |
y = ln(kx +b) |
y | |
Приложение производной к исследованию функций
Не знаю
Первообразная функции и неопределенный интеграл
Основной задачей дифференциального исчисления является нахождение производной f '(x) или дифференциала f '(x)dx данной функции f(x) В интегральном исчислении решается обратная задача: Дана функция f(x); требуется найти такую функцию F(x), производная которой равна f(x) или дифференциал которой равен f(x)dx в области определения функции f(x), т.е. в этой области функции f(x) и F(x) связаны соотношением
F'(x)=f(x)
или
dF(x)= F'(x)dx= f(x)dx
Определение 1: Функция F(x) называется первообразной функцией для данной функции f(x), если для любого x из области определения f(x)выполняется равенство F'(x)= f(x) или dF(x)= f(x)dx Из дифференциального исчисления известно что если две функции f(x) и (x) отличаются друг от друга на постоянную величину, то производные или дифференциалы этих функций равны, т.е. если
f(x) = (x) + C
то
f '(x) = '(x)
или
f '(x)dx = '(x)dx
Известно также, что, и наоборот, если две функции f(x) и (x) имеют одну и ту же производную или один и тот-же дифференциал, то они отличаются друг от друга на постоянную величину, т.е. если
f '(x) = '(x) или df(x) = d(x),
то
f(x) = (x) + С
Отсюда непосредственно следует, что если в формуле y = F(x) + C мы будем придавать постоянной C все возможные значения, то получим все возможные первообразные функции для функции f (x) Определение 2: Множество F(x) + C всех первообразных функций для данной функции f (x) , где C принимает все возможные числовые значения, называется неопределенным интегралом от функции f (x) и обозначается символом
![]()
Таким образом, по определению,
![]()
где F'(x)
= f (x) или dF(x)
= f(x)dx и С -
произвольная постоянная. В последней
формуле f(x) называется подинтегральной
функцией, f(x)dx- подинтегральным
выражением,
а символ ![]() -
знаком неопределенного
интеграла.
Неопределенным
интегралом называют не только множество
всех первообразных, но и любую функцию
этого множества.
Таким
образом, неопределенный
интеграл представляет собой любую
функцию, дифференциал которой равен
подинтегральному выражению, а производная
равна подинтегральной функции
Нахождение
первообразной по данной
функции f(x) называется интегрированием и
является действием, обратным
дифференцированию.
-
знаком неопределенного
интеграла.
Неопределенным
интегралом называют не только множество
всех первообразных, но и любую функцию
этого множества.
Таким
образом, неопределенный
интеграл представляет собой любую
функцию, дифференциал которой равен
подинтегральному выражению, а производная
равна подинтегральной функции
Нахождение
первообразной по данной
функции f(x) называется интегрированием и
является действием, обратным
дифференцированию.
Определенный интеграл и его основные свойства. Формула Ньютона-Лейбница
Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Определенный интеграл от функции f (x) в пределах от a до b вводится как предел суммы бесконечно большого числа слагаемых, каждое из которых стремится к нулю:
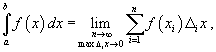
где
![]()
Свойства определенного интеграла
Ниже предполагается, что f (x) и g (x) - непрерывные функции на замкнутом интервале [a, b].
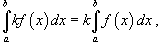 где k -
константа;
где k -
константа;
Если
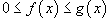 для
всех
для
всех 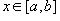 ,
то
,
то 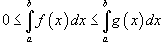 .
.
Если
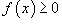 в
интервале [a,
b], то
в
интервале [a,
b], то 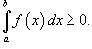
Формула Ньютона-Лейбница
Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Если F (x) - первообразная функции f (x) на[a, b], то
![]()
Площадь криволинейной трапеции
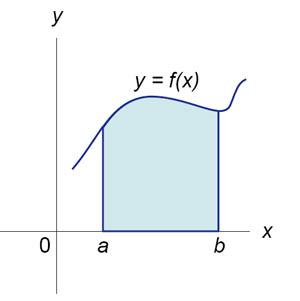
Площадь фигуры, ограниченной осью 0x, двумя вертикальными прямыми x = a, x = b и графиком функцииf (x) (рисунок 1), определяется по формуле
![]()
|
|
|
|
|
Рис.1 |
|
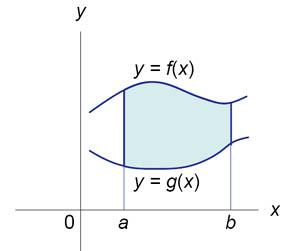
Рис.2 |
Пусть F (x) и G (x) - первообразные функций f (x) и g (x), соответственно. Если f (x) ≥ g (x) на замкнутом интервале [a, b], то площадь области, ограниченной двумя кривыми y = f (x), y = g (x) и вертикальными линиями x = a, x = b (рисунок 2), определяется формулой
![]()
Замена переменной в определенном интеграле
Определенный
интеграл 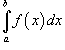 по
переменной x можно
преобразовать в определенный интеграл
относительно переменной t с
помощью подстановки x
= g (t):
по
переменной x можно
преобразовать в определенный интеграл
относительно переменной t с
помощью подстановки x
= g (t):
![]()
Новые пределы интегрирования по переменной t определяются выражениями
![]()
где g -1 - обратная функция к g, т.е. t = g -1(x).
Интегрирование по частям для определенного интеграла
В этом случае формула интегрирования по частям имеет вид:
![]()
где ![]() означает
разность значений произведения
функций uv при x
= b и x
= a.
означает
разность значений произведения
функций uv при x
= b и x
= a.
Методы интегрирования
Точное нахождение первообразной (или интеграла) произвольных функций — дело гораздо более сложное, чем дифференцирование, то есть нахождение производной. Зачастую выразить интеграл в элементарных функциях невозможно.