
ShashenkoSzdvigkovaGapeev_monograf
.pdf
РАЗДЕЛ 7
|
|
|
2P |
|
|
|
|
|
|
|
|
|
|
||||
ϕ(ξ)+ϕ(ξ) = k A − B + |
0 |
|
− 2kBln |
ω(ξ) ω(ξ) , |
(7.17) |
|||
k |
||||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A − B[ω |
(ξ) |
|
|
] |
|
|
|
|
|
|
|
|
|
|
|
|||||
ω(ξ) |
′ |
|
|
|
|
|
|
|
|
|
ω(ξ) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
ϕ (ξ)+ψ |
(ξ)= 2k |
|
|
|
|
|
|
|
|
|
|
|
, |
ξ |
|
=1, |
|
|
(7.18) |
|||||||||||||
|
|
|
|
ω (ξ) |
|
|
|
[ω(ξ)] |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
при |
|
ξ |
|
→ ∞ |
ϕ(ξ)= |
1 |
|
(σx∞ +σ y∞ )+ O(ξ −2 ), |
|
|
|
|
|
|
|
|
|
|
(7.19) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
ψ (ξ)= |
|
1 |
(σx∞ −σy∞ )+O(ξ−2 ), |
|
|
|
|
|
|
|
|
|
|
(7.20) |
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
ω(ξ) = O(ξ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.21) |
||||||||||||||
|
|
Рассмотрим в расширенной плоскости ξ функциональное уравнение |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
ϕ′(ξ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A − B ω(ξ)ω |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
ξ |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
+ψ(ξ)= k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
(7.22) |
||||||||||
|
|
|
|
|
|
|
|
ω (ξ) |
ξ |
|
|
|
[ω(ξ)] |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
решение которого будем искать в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
ω(ξ)= C3ξ + Pv |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.23) |
|||||||||||||||
|
|
|
|
|
|
|
|
ξ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Здесь Pv ξ1 – полином v -й степени с неопределенными пока коэффициентами.
Подставляя формально выражение (7.23) в основное уравнение (7.22) и раскладывая все функции в ряд в окрестности бесконечно удаленной точки, получаем, что v =1. Тогда
ω(ξ)= C ξ + |
C4 |
, |
(7.24) |
|
|||
3 |
ξ |
|
|
|
|
|
где C3 , C4 – неизвестные константы, действительные из условия симметрии.
Для определения неизвестных постоянных рассмотрим в расширенной плоскости ξ функциональное уравнение (7.17). Обозначим правую его часть
160

ЧИСЛЕННЫЕ РЕШЕНИЯ УПРУГО-ПЛАСТИЧЕСКИХ ЗАДАЧ ПРИМЕНИТЕЛЬНО К УСТОЙЧИВОСТИ ПОДЗЕМНЫХ ВЫРАБОТОК
через f (ξ), внешность единичного круга с контуром L |
через S − , внутреннюю |
||
1 |
|
||
часть единичного круга через S + . Тогда уравнение (7.17) примет вид |
|||
ϕ(ξ)+ |
|
= f (ξ). |
(7.25) |
ϕ(ξ) |
|||
Умножим каждое слагаемое выражения (7.25) на ядро Коши и проинтегрируем их по контуру L1 . Получим
|
1 |
|
ϕ(ξ) |
|
|
|
|
|
|
|
|
dξ = |
1 |
L∫ |
f (ξ) |
dξ , |
|
|||
|
L∫ |
dξ + |
1 |
L∫ |
ϕ(ξ) |
(7.26) |
||||||||||||||
|
2πi |
ξ − Z |
2πi |
ξ − Z |
|
2πi |
ξ − Z |
|||||||||||||
1 |
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
||||||
где Z S −, ξ L . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Исходя из того, что функция ϕ(ξ) |
голоморфна вне L1 , непрерывна на L1 и |
|||||||||||||||||||
является граничным значением функции ϕ(Z ) при Z →ξ , получим, что первое |
||||||||||||||||||||
слагаемое в выражении (7.26) равно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
L∫ |
ϕ(ξ) |
dξ = 0 ; |
|
Z S − . |
(7.27) |
||||||||||
|
|
|
|
2πi |
ξ − Z |
|
||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Функция ϕ(ξ) в нашем случае удовлетворяет условиям теоремы Коши для бес-
конечной области [258], в соответствии с чем второе слагаемое в (7.26) равно:
|
|
|
1 |
|
|
|
|
|
|
|
|
|
L∫ |
ϕ(ξ) |
|
dξ = −ϕ(Z )+ϕ(∞). |
(7.28) |
||
|
|
|
2πi |
ξ − Z |
|
||||
|
|
1 |
|
|
|
|
|
||
Если функция |
f (Z ) |
голоморфна в S − , непрерывна в (S − + L ) |
за исклю- |
||||||
|
|
|
|
|
1 |
|
|||
чением, быть может, конечных точек а1, а2, а3….а4 этой области, а также точки Z = ∞, где она может иметь полюс с главными частями G1 (Z ), G2 (Z ),...Gn (Z ),
G∞ (Z ), то она может быть представлена следующим образом
1 |
∫ |
|
f (ξ) |
dZ = − f (Z )+ G (Z )+ G |
(Z ); |
Z S − , |
(7.29) |
||||
|
|
|
|||||||||
|
ξ − Z |
1 |
|
|
∞ |
|
|
|
|||
2πi L |
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
∫ |
|
f (ξ) |
dξ = G (Z )+... + G |
n |
(Z )+ G |
(Z ); |
Z S + . |
(7.30) |
||
|
|
|
|||||||||
|
ξ − Z |
1 |
|
|
∞ |
|
|
||||
2πi L |
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
|
161

РАЗДЕЛ 7
Раскроем правую часть уравнения (7.26):
|
|
|
|
|
|
|
|
|
|
|
|
A − B + |
2P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
f (ξ) |
|
2k |
|
|
0 |
|
2Bk |
|
|
|
lnω(ξ) |
|
|
2Bk |
∫ |
ln |
|
|
dξ . (7.31) |
||||||||||||||||
|
|
|
|
|
|
|
∫ |
dξ − |
|
ω(ξ) |
||||||||||||||||||||||||||||
|
∫ |
dξ = |
|
∫ |
k |
dξ − |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2(ξ − 2) |
4πi |
|
|
|
4πi |
|
|
|
|
||||||||||||||||||||||
|
2πi L |
ξ − Z |
|
2πi L |
|
L |
ξ − Z |
|
|
|
L ξ − Z |
|||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||
|
Первые два слагаемые в выражении (7.31) удовлетворяют условиям (7.29) |
|||||||||||||||||||||||||||||||||||||
и (7.30), поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2P |
|
|
|
2P0 |
|
|
|
|
|
2P |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
1 |
|
|
A − B + |
|
|
0 |
|
|
− A − B |
+ |
|
|
|
|
|
|
A |
− B + |
0 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
L∫ |
|
k |
dξ = |
|
|
|
|
|
|
+ |
|
|
|
k |
|
= 0 при Z → ∞, |
||||||||||||||||||
|
|
|
|
2πi |
2(ξ − Z ) |
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
∫ |
lnω(ξ) |
dξ |
= lnω + G∞ (Z )= −lnω + lnC3Z = −ln |
ω |
. |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
2πi L |
ξ − Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
Z |
||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|||
Третье слагаемое в выражении (7.31) равно нулю по той же причине, что и (7.27). Таким образом, получаем
−ϕ(Z )+ϕ(∞)= − |
1 |
ln |
ω(Z ) |
, |
Z S − . (7.32) |
|
2 |
C3Z |
|||||
|
|
|
|
Из граничного условия (7.19) при Z →ξ для функции ϕ(ξ) находим
ϕ(ξ)= 0,25γH (1 + λ)− Bk ln ω(ξ).
C3ξ
Из уравнения (7.22) следует, что
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
A − B[ω(ξ) ω(ξ)] |
|
|
|
|
1 |
|
|||||
|
|
|
|
|||||||||
ψ (ξ)= 2k |
|
|
|
|
− |
|
|
ω |
|
. |
||
[ω(ξ)] |
ω (ξ) |
|
||||||||||
|
|
|
|
|
ξ |
|
||||||
|
2 |
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Учитывая, что
(7.33)
(7.34)
ω(ξ)= C3ξ + |
C4 |
|
|
|
1 |
|
C3 |
+ C4 , |
′ |
C4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
ω |
|
|
|
|
|
|
|
|
|
|||||
|
; |
= |
|
|
|
|
|
|
, |
|||||||
ξ |
ξ |
ϕ (ξ)= − |
ξ(C ξ2 |
+ C |
|
) |
||||||||||
|
|
|
|
|
ξ |
|
|
|
4 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
получим
162

ЧИСЛЕННЫЕ РЕШЕНИЯ УПРУГО-ПЛАСТИЧЕСКИХ ЗАДАЧ ПРИМЕНИТЕЛЬНО К УСТОЙЧИВОСТИ ПОДЗЕМНЫХ ВЫРАБОТОК
ψ(ξ)= 2k |
A − B[C 2 |
+ C 2 |
|
+ C |
C |
(ξ2 |
+ξ−2 )] |
|
C |
(C ξ2 |
+ C |
) |
|
|
|||||
3 |
4 |
|
3 |
4 |
|
|
|
|
|
+ |
4 |
4 |
|
3 |
|
|
. |
(7.35) |
|
C 2ξ |
2 + C |
2ξ−2 + 2C |
C |
4 |
|
C 2ξ4 |
− C 2 |
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
3 |
4 |
|
|
3 |
|
|
|
|
|
3 |
|
1 |
|
|
|
|
||
Таким образом, поставленная задача решена с точностью до постоянных интегрирования.
Отметим, что при ξ → ∞ ψ(ξ)= −kB |
C4 |
. С другой стороны, из (7.20) сле- |
|
C3 |
|||
|
|
дует, что при ξ → ∞ ψ(ξ)= 0,5γH (1 − λ).
Приравнивая эти два выражения, находим:
C4 |
= C3 γH (1 − λ). |
|
|
|
|
|
(7.36) |
||||||
|
|
|
2Bk |
|
|
|
|
|
|
|
|
||
В соответствии с теоремой о среднем для гармонической функции |
|||||||||||||
∫ϕ(ξ)+ |
|
|
dξ = 0 . |
|
|
|
|
|
|
||||
ϕ(ξ) |
|
|
|
|
|
(7.37) |
|||||||
L |
2ξ |
|
|
|
|
|
|
|
|
||||
Образуем функцию, сопряженную (7.33), |
и проинтегрируем |
Re f (ξ) со- |
|||||||||||
гласно (7.37). Ту же процедуру выполним для уравнения (7.34). |
|
||||||||||||
Приравнивая полученные выражения, найдем постоянную С3: |
|
||||||||||||
C3 |
= exp |
A |
− |
γH |
(1 |
+ λ)+ |
P0 |
− |
1 |
. |
(7.38) |
||
|
|
|
|
||||||||||
|
|
2B |
4Bk |
|
2B |
2 |
|
||||||
Таким образом, постоянные интегрирования определены. Граница L между упругой областью и областью разрушения представляет собой эллипс, уравнение которого имеет вид
X 2 |
|
Y 2 |
|
|
|
+ |
|
=1, |
(7.39) |
C32 (1 + β)2 |
C32 (1 − β)2 |
|||
где
β = γH (1 − λ). 2Bk
163
РАЗДЕЛ 7
|
Конечные |
выражения |
|
такого решения отличаются |
|
|
существенной сложностью, |
|
|
что затрудняет их исследо- |
|
|
вание и практическое ис- |
|
|
пользование. В [232], осно- |
|
|
вываясь на работах Ж.С. |
|
|
Ержанова, делается вывод о |
|
|
том, что в пределах верхне- |
|
|
го слоя литосферы, где, |
|
|
собственно, и ведутся гор- |
|
|
ные работы, в горизонталь- |
|
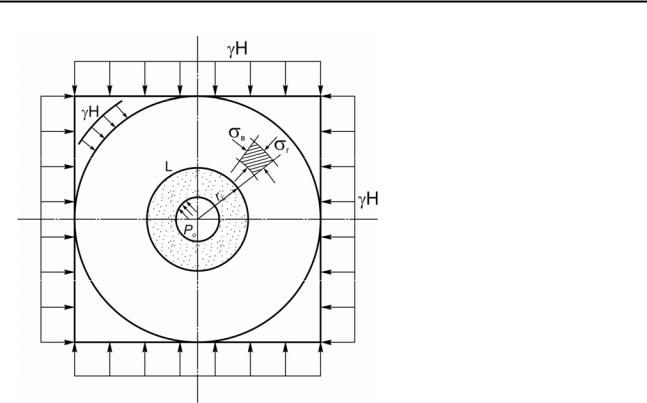
Рис. 7.2. Расчетная схема к решению задачи |
но залегающих |
осадочных |
о равновесии породного массива в окрестности |
породах для широкого диа- |
|
одиночной горизонтальной выработки (λ=1) |
пазона горно-геологических |
|
|
условий можно считать, что |
|
напряжения в нетронутом породном массиве распределены гидростатически, т.е. λ=1. В этом случае решение поставленной задачи существенно упрощается, поскольку контур эллипса L вырождается в круг. Расчетная схема, используемая для решения задачи, приведена на рис. 7.2.
Для рассматриваемой одномерной задачи запишем в полярной системе координат исходные соотношения:
– уравнение равновесия
|
dσr |
|
− |
σθ |
−σr |
= 0 |
; |
|
|
|
(7.40) |
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
dr |
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
– уравнение совместности деформаций |
|
|
|
|
|
|
|||||||||||||
|
d 2ε |
θ |
|
+ |
2 |
|
|
|
dε |
θ |
− |
1 |
|
dε |
r |
= 0 ; |
(7.41) |
||
|
dr 2 |
|
r |
|
dr |
r |
dr |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
– соотношения Гука
164

ЧИСЛЕННЫЕ РЕШЕНИЯ УПРУГО-ПЛАСТИЧЕСКИХ ЗАДАЧ ПРИМЕНИТЕЛЬНО К УСТОЙЧИВОСТИ ПОДЗЕМНЫХ ВЫРАБОТОК
εr = |
1 |
[(1 − μ)σr − μσθ ], |
(7.42) |
|||||
|
2G |
|||||||
|
|
|
|
|
|
|
|
|
εθ = |
1 |
|
[(1 − μ)σθ − μσr ]; |
(7.43) |
||||
|
2G |
|||||||
|
|
|
|
|
|
|
|
|
– соотношения Коши |
|
|
|
|
|
|
|
|
εr = |
dU |
|
; |
εθ = |
U |
, |
(7.44) |
|
dr |
|
|
||||||
|
|
|
|
|
r |
|
||
где σr , σθ и εr , εθ – соответственно радиальный и тангенциальный компо-
ненты напряжений и деформаций, U – радиальное перемещение, G – модуль сдвига, μ – коэффициент Пуассона, r – полярная координата.
Здесь и далее все величины, имеющие размерность длины и перемещений, по-прежнему отнесены к радиусу выработки Rо. Граничные условия и условия
сопряжения имеют вид: |
|
|
|
|
|
|
|
σr |
=σθ =γH |
|
при r → ∞, |
(7.45) |
|||
σr |
= P0 |
|
|
|
при r =1, |
(7.46) |
|
σ |
r |
=σ (1) |
, U |
r |
=U (1) |
при r = r . |
(7.47) |
|
r |
|
r |
L |
|
||
Будем обозначать все компоненты напряжений и перемещений в упругой области без индекса, а в пластической – с индексом 1.
Решив уравнение Эйлера, полученное из (7.41), удовлетворяя граничным условиям (7.45), получим формулы для определения компонентов напряжений в упругой области
σr =γH − |
C |
; |
σθ =γH + |
C |
, |
(7.48) |
|
r 2 |
r 2 |
||||||
|
|
|
|
|
где С – неизвестная постоянная интегрирования, определяемая из условий сопряжений радиальных напряжений на контуре L (7.47).
В области неупругих деформаций справедливо физическое уравнение:
σθ −σr = 2k |
A |
− B |
, |
(7.49) |
|
||||
r 2 |
|
|
|
|
165

РАЗДЕЛ 7
где k – некоторая константа, зависящая от исходных физических предпосылок, заложенных в условие прочности, определяемая в нашем случае выражением (3.10); А и В – константы, которые можно установить на основе выражений
(2.15).
Решая это уравнение совместно с уравнением равновесия (7.40), получим с учетом граничных условий (7.46) выражения для компонентов напряжений в пластической области
σ (1) |
= −2k[0,5A(r −2 |
−1)+ B ln r]+ P , |
(7.50) |
r |
|
0 |
|
σ (1) |
= −2k[0,5A(r −2 |
+1)+ Bln r]+ P . |
(7.51) |
θ |
|
0 |
|
При r = rL , учитывая равенство радиальных напряжений, определяемых формулами (7.48) и (7.50), получим значение неизвестной постоянной интегри-
рования C = krL2 .
Таким образом, компоненты напряжений в упругой и пластической областях определены. Тогда, используя (7.47), (7.50), получим трансцендентное выражение для определения радиуса области неупругих деформаций:
0,5A(r −2 |
−1)+ B ln r |
= |
γH − P0 |
− |
1 |
. |
(7.52) |
|
|
||||||
L |
L |
2k |
2 |
|
|
||
|
|
|
|
|
|||
Из (7.52) следует, во-первых, что отпор крепи Ро чрезвычайно мало влияет на размеры области неупругих деформаций, поскольку величина его на глубоких горизонтах шахт несоизмеримо меньше гравитационного давления γH . В
этой связи в формуле (7.52) без ущерба для точности можно положить Ро=0. Во-вторых, для подавляющего большинства углевмещающих горных пород величина ψ , входящая в выражение (3.10), приблизительно равна 0,1, и если по-
ложить ее в таком случае равной нулю, то ошибка от подобной идеализации не превысит 5 %.
166

ЧИСЛЕННЫЕ РЕШЕНИЯ УПРУГО-ПЛАСТИЧЕСКИХ ЗАДАЧ ПРИМЕНИТЕЛЬНО К УСТОЙЧИВОСТИ ПОДЗЕМНЫХ ВЫРАБОТОК
|
|
|
|
|
R k |
c |
|
Основываясь на анализе зависимостей r |
= f |
c |
для различных значе- |
||||
|
|
||||||
|
|
|
L |
|
γH |
||
|
|
|
|
||||
ний коэффициента остаточной прочности kост |
(см. раздел 2.1), приведенном в |
||||||
[232], положим, что kост =0. Тогда, |
окончательная формула для определения |
||||||
радиуса области неупругих деформаций на основе (7.52) примет вид |
|||||||
r 2 ln r |
γH |
. |
|
|
(7.53) |
||
L |
L = |
R k |
|
|
|||
r 2 |
−1 |
c |
|
|
|
|
|
L |
|
c |
|
|
|
|
|
Используя соотношения Коши нения (2.19), учитывая, что εr +εθ
альное уравнение:
(7.44), выражение для функции разупроч- =εv , получим неоднородное дифференци-
dU |
+ |
U |
= ε* 1+ B − |
A |
|
, |
|
dr |
r |
r2 |
|||||
|
v |
|
|
где εv* – предельная объемная деформация в условиях одноосного сжатия.
Решение соответствующего однородного уравнения имеет вид:
U = C r−1 .
(7.54)
(7.55)
Варьируя постоянную, получим с учетом равенства радиальных перемещений на контуре L выражение для определения перемещений в пластической области:
U = |
εv* (B +1) (r2 |
− r2 )− 2Aln |
r |
. |
(7.56) |
|
|
||||||
|
2r |
|
L |
r |
|
|
|
|
|
|
L |
|
|
С учетом (7.53) и (2.15) при kост = 0 получим выражение для определения смещений на контуре выработки:
U |
|
=ε |
* |
|
0,5 |
− |
γH |
|
(7.57) |
|
|
|
R k |
. |
|||||
|
0 |
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
c |
|
167

РАЗДЕЛ 7
Основные зависимости для определения параметров упругопластического состояния породного массива в окрестности одиночной выработки (7.53) и (7.57), полученные выше, позволяют определить некоторые (точечные) значения вероятностных по своей природе величин: радиуса области неупругих деформаций rL и радиальных смещений на контуре выработки U0.
Определим радиус области неупругих деформаций и величину перемещений контура выработки для средних условий Западного Донбасса при следующих исходных данных:
–глубина расположения выработки Н= 350 м;
–предел прочности на одноосное сжатие c = 25 МПа;
–объемная плотность, = 2,50 10-3 МН/м3;
–радиус выработки R0 = 2,0 м;
–коэффициент структурно-механического ослабления kc = 0,33;
–предельное значение объемной деформации в условиях одноосного сжа-
тия v*= −0,1.
Согласно выражениям (7.53) и (7.57), для этих условий получим, что rL 2,3, а U0 0,38 м.
7.2. Алгоритм численного решения упругопластической задачи
Из испытаний на одноосное сжатие в условиях заданных деформаций из-
вестно, что существует некоторое предельное напряжение сжатия Rc ,
вплоть до достижения которого материал деформируется практически по линейному закону. Диаграмма деформирования « » становится все более пологой в окрестности точки Rc, c , где Rc – предел прочности на одноосное сжатие, c – деформация, соответствующая Rc . В самой точке Rc, c d 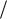 d 0, после чего деформирование характеризуется ниспадающей ветвью,
d 0, после чего деформирование характеризуется ниспадающей ветвью,
которая имеет отрицательную кривизну d2 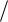 d 2 0 и стремится к некоторым остаточным напряжениям и деформациям разрушения R*, * . Обобщенный
d 2 0 и стремится к некоторым остаточным напряжениям и деформациям разрушения R*, * . Обобщенный
168
ЧИСЛЕННЫЕРЕШЕНИЯ УПРУГО-ПЛАСТИЧЕСКИХ ЗАДАЧ ПРИМЕНИТЕЛЬНО К УСТОЙЧИВОСТИ ПОДЗЕМНЫХ ВЫРАБОТОК
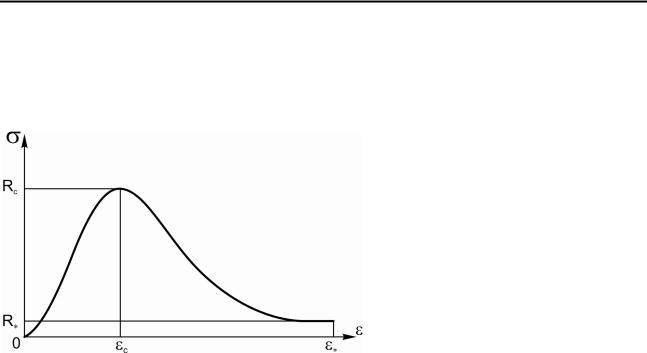
вид диаграммы деформирования в соответствии с исследованиями, изложенными в разделе 2, показан на рис. 7.3.
В работе [259] показано, что наличие ниспадающей ветви диаграммы деформирования (т.е. участка разупрочнения) приводит к тому, что в области разрыхления так называемое условие сверхустойчивости по Адамару, приведенное в работе [260], не выполняется, что с теоретической точки зрения приводит к неединственности решения
краевой задачи. При использовании численных методов это означает, что система уравнений относительно перемещений становится вырожденной, в результате чего вычислительный процесс не может быть продолжен. Таким образом, ни одна из «традиционных» моделей деформирования сплошных сред, в том числе и нелинейная теория упругости, в данном случае неприменимы. В работе [261] была предложена модель пошагового «упругого» решения рассматриваемой задачи. Данная модель является аналогом известного в механике деформируемого твердого тела метода упругих решений, который часто применяется для решения краевых упругопластических задач с упрочнением. Схематически этот метод изложен, например, в [262].
Необходимо отметить, что численная модель, предложенная в 261 , не лишена некоторых упрощений и идеализации. Например, в ней учитывалась только «верхняя» часть полной диаграммы деформирования горных пород, отражающая продольные деформации образца, нагружаемого в режиме заданных деформаций, и не учитываются полные, объемные, деформации. Это приводит
169
