
Практикум по механике и молекулярной физике
.pdf
определенный объем воды, выключают секундомер. По термометру определяют температуру Т, по барометру – давление P окружающей среды.
По формулам (4) и (5) вычисляют λ |
и |
. Манометр заполнен спир- |
||||||||||
том, плотность |
которого |
d = 0,78 103 |
кг/м3. |
Для данного капилляра |
||||||||
l = (0,1025 0,0005) м, r |
= (0,65 0,01) 10-3 м. Цена деления сосуда |
|||||||||||
V0 = 50 10–6 |
м3/дел. По |
барометру |
давление |
дается |
в |
мм |
рт. |
cт. |
||||
(1 мм рт. ст. = 1330 Н/м2). |
|
|
|
|
|
|
|
|
|
|
||
Результаты измерений заносятся в таблицу. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
№ п/п H,M h,M |
2 |
( р) м/Н t,c |
t,c |
V,M |
3 |
,M |
, M |
/ 100%· |
,кг/м |
кг/м с |
/ |
100% |
P,/м |
V,M |
|||||||||||
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
1
2
3
Ср.
Контрольные вопросы
1.Дайте определение длины свободного пробега молекул. От чего зависит длина свободного пробега молекул газа?
2.Как известно, воздух состоит из смеси газов. Что следует в этом случае понимать под средней длиной свободного пробега?
3.Почему коэффициент внутреннего трения жидкостей убывает с температурой, а у газов возрастает?
4.Какие существуют скорости молекул газа? Расскажите о максвелловском законе распределения молекул по скоростям.
РАБОТА № 9
ОПРЕДЕЛЕНИЕ МОДУЛЯ ЮНГА МЕТОДОМ ПРОГИБА
Принадлежности: станина с опорными призмами, индикатор с механизмом часового типа, линейка, штангенциркуль, набор стержней прямоугольного сечения.
Краткая теория
Все твердые тела характеризуются механическими свойствами, которыми определяется их способность изменять свою форму (деформироваться) под действием внешних механических сил. Деформация твердого тела является результатом изменения под действием внешней силы взаимного расположения частиц, из которых состоит тело, и расстояний между ними. Деформация называется упругой, если она исчезает после прекращения действия силы, и пластической, если она сохраняется и после прекращения нагрузки. Все твердые тела могут быть деформированы и упруго, и пластически. При малых силах твердые тела деформируются упруго.
61
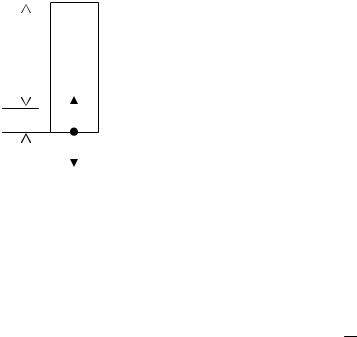
Рассмотрим более подробно упругую деформацию, которую всегда учитывают при расчете различных технических сооружений для их длительной работы. Как уже отмечалось, сила может деформировать твердое тело: смещать составляющие его частицы относительно друг друга. При этом (в соответствии с третьим законом Ньютона) внутри деформированного тела возникает противодействующая сила, равная по модулю деформирующей силе и называемая силой упругости. Эта сила стремится как бы восстановить первоначальную форму и объем твердого тела. Деформации, которые может испытывать твердое тело под действием приложенной внешней силы, сводятся к двум основным видам: растяжению или сжатию и сдвигу. Соотношение между силой упругости и деформацией определяется законом Гука: сила упругости F, возникающая при малых деформа-
циях любого вида, пропорциональна деформации (смещению) |
x , т. е. |
F = −k x, |
(1) |
где k – коэффициент пропорциональности, зависящий от вида деформации. Знак минус указывает на противоположность направлений силы упругости и смещения. При больших смещениях x возникает остаточная деформация – тело не восстанавливает полностью свою форму и размер и даже может произойти его разрушение. Выясним теперь, как записывается закон Гука для одного из основных видов деформации – одностороннего растяжения (сжатия). Пусть к нижнему концу закрепленного стержня длиной ℓ и площадью поперечного сечения S приложена деформирующая си-
|
|
|
|
|
|
|
ла F1. Тогда в нем возникает сила упругости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F = – F1 (рис. 1). |
|
|
A |
|
|
|
|
Под действием внешней силы длина |
|
|
|
|
|
|
стержня увеличится на некоторую величину ∆ℓ. |
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
Но это удлинение ∆ℓ не может быть принято за |
|
∆A |
|
|
|
|
характеристику деформации, т. к. сила действу- |
||
|
|
|
|
||||
|
|
|
|
|
|
|
ет на каждую единицу длины ∆ℓ стержня, а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
длина стержня может быть разной. Поэтому уд- |
|
|
|
|
F1 |
линение ∆ℓ будет определяться не только дей- |
||
|
|
|
|
Рис. 1 |
ствующей силой, но и первоначальной длиной |
||
|
|
|
|
|
|
|
стержня. В качестве величины деформации не- |
обходимо брать отношение ∆ℓ/ℓ, которое уже от ℓ не зависит. Это отношение называется относительным удлинением. Опыт показывает, что если в деформированном теле выделить некоторую произвольную поверхность, то деформация определяет не силу, действующую на эту поверхность, а
отношение этой силы к площади поверхности FS =σ, которая называется
напряжением (измеряется она в тех же единицах, как и давление). Теперь закон Гука для одностороннего растяжения (а равно как и для сжатия, только с заменой знаков) можно записать в виде:
62
σ = |
F |
= E |
A. |
(2) |
|
S |
|
A |
|
Величина Е называется модулем Юнга или модулем упругости. Записав
формулу закона Гука (2) в виде |
σ |
= E, |
(3) |
|
A/ A |
||||
|
|
|
можно определить физический смысл модуля Юнга. Если в (3) положить ∆ℓ/ℓ = 1 (т. е. удвоить длину), то σ = Ε. Отсюда следует, что модуль Юнга Е численно равен напряжению , которое растягивает стержень вдвое. Такое определение модуля Юнга носит отвлеченный характер, ибо в действительности линейная зависимость между деформацией и напряжением наблюдается только при малых деформациях ( A / A << 1), и подавляю-
щее большинство материалов разрушается значительно раньше, чем будет достигнуто напряжение, численно равное модулю Юнга. Модуль Юнга – одна из существенных констант, характеризующих упругие свойства вещества.
Всистеме СИ модуль Юнга измеряется в Н/м2 (Па), а в системе СГС –
вдин/см2. При одностороннем растяжении или сжатии изменяется не только длина стержня, но и его поперечные размеры, т.е. его радиус. Если
эту деформацию характеризовать относительным изменением радиуса rr ,
то можно записать |
σ |
= M , |
(4) |
|
r / r |
||||
|
|
|
где М – коэффициент пропорциональности, который можно назвать модулем поперечного сжатия при продольном растяжении. Ясно, что между A / A и r / r должна быть простая связь. Она выражается в том, что их отношение есть величина постоянная для данного вещества:
r / r |
= μ. |
(5) |
A/ A |
|
|
Постоянная называется коэффициентом Пуассона и равна отношению поперечного и продольного удлинений.
Описание установки
В нашей задаче метод определения модуля Юнга основан на измерении стрелы прогиба при деформации изгиба однородного стержня, лежащего на двух опорах, если к его середине приложена сосредоточенная сила Р. Если мысленно разбить стержень на тонкие продольные слои, то при изгибе его они окажутся различной длины. Нижние слои при этом удлиняются, верхние укорачиваются. Нейтральная линия среднего слоя сохраняет свою длину. Таким образом, деформация изгиба сводится к деформации одностороннего растяжения и сжатия. Перемещение, которое получит середина стержня под действием груза Р, называется стрелой прогиба . Теоретиче-
63
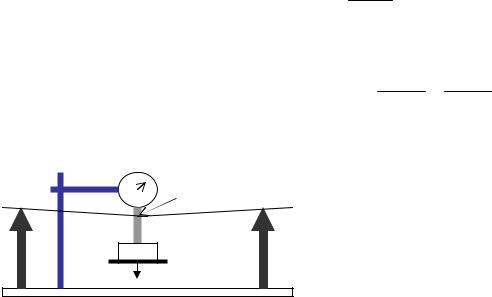
ские исследования деформации изгиба в нашем случае дают формулу для |
|||||||
вычисления стрелы прогиба: |
|
λ = |
PL3 , |
|
(6) |
||
|
|
|
4Eab3 |
|
|
||
где Р – вес груза, приложенный в центре стержня, Е – модуль Юнга, |
a – |
||||||
ширина, b – толщина, L – длина стержня. Из (6) следует формула для оп- |
|||||||
ределения модуля Юнга |
|
|
E = |
PL3 |
= mgL3 , |
(7) |
|
|
|
|
|
4λab3 |
4λab3 |
|
|
где m - масса груза, g - ускорение свободного падения. |
|
||||||
|
|
|
Прибор для определения модуля |
||||
1 |
|
Юнга (рис. 2) состоит из массивной |
|||||
2 |
3 |
станины 6 с двумя стойками, на кон- |
|||||
цах которых имеются стальные опор- |
|||||||
|
|||||||
5 |
4 |
ные призмы 4, ребра которых парал- |
|||||
|
лельны. На ребра этих призм кладут |
||||||
|
6 |
||||||
Р |
испытуемый стержень 3, а к его сере- |
||||||
Рис. 2 |
|
дине подвешивают рамку 2, верхняя |
|||||
|
сторона которой представляет собой |
||||||
|
|
||||||
призму, обращенную ребром вниз. |
Этим ребром рамка опирается на стер- |
||||||
жень. Рамка несет на себе платформу 5 для гирь, с помощью которых соз- |
|||||||
дается изгибающая сила. На специальной стойке укрепляют индикатор 1, |
|||||||
подводя его щуповой механизм к середине стержня до соприкосновения. |
|||||||
Индикатор имеет механизм часового типа, в котором поступательное пе- |
|||||||
ремещение щупа преобразуется в заметный поворот стрелки индикатора. |
|||||||
Индикатор имеет цену деления 0,01 мм, и один оборот стрелки, равный |
|||||||
100 делениям, соответствует 1 мм поступательного движения щупа. Шкалу |
|||||||
индикатора можно поворачивать, что дает возможность устанавливать |
|||||||
против стрелки нуль шкалы при любом положении щупа. |
|
||||||
Выполнение работы
1.Измерить линейкой расстояние L между опорными призмами.
2.Измерить штангенциркулем ширину a и толщину b стержня. Каждый размер определяется три раза в разных местах стержня и берется среднее значение.
3.Нагрузить платформу последовательно грузами массой (1,0 0,001)
кг и (0,5 0,01) кг.
4.Установить щуп индикатора таким образом, чтобы он касался
рамки.
5.Совместить нуль шкалы со стрелкой индикатора.
6.Снять с платформы груз 0,5 кг и определить стрелу прогиба для этого груза. Повторить эту операцию трижды и взять среднее значение.
7.Проделать то же с грузом 1,0 кг.
8.Такие измерения провести с другим стержнем.
64

9. Данные опыта занести в таблицы, по формуле (7) вычислить модуль Юнга для каждого груза и погрешности измерений.
Данные измерений для первого стержня
|
|
|
|
|
|
|
m1= |
|
m2= |
|
|
|
|
|
||
№n/n |
|
|
|
|
|
|
0,5кг |
|
1,0кг |
|
|
.,ЕсрН/м |
2 |
|||
ммL, |
ммL, |
мм,а |
|
ммb, |
|
|
|
|
|
Е |
Е |
Еср.,Нм/ |
||||
|
|
|
|
|
|
мм |
|
|
мм |
мм |
|
мм |
м / Н |
м / Н |
2 |
|
|
|
|
|
ммa |
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
b |
мм1, |
|
1, |
2, |
|
2, |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
, |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ср |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для данных измерений для другого стержня таблица аналогична.
Контрольные вопросы
E 100%
Eсс.
1.Сформулируйте и запишите закон Гука.
2.Запишите и объясните формулу закона Гука для деформаций растяжения и сдвига.
3.В чем физический смысл модуля Юнга и коэффициента Пуассона?
4.Объясните зависимость модуля Юнга от природы вещества и температуры.
РАБОТА № 10
ОПРЕДЕЛЕНИЕ МОДУЛЯСДВИГАИЗКРУТИЛЬНЫХКОЛЕБАНИЙ
Принадлежности: прибор для определения модуля сдвига из крутильных колебаний, секундомер, микрометр, масштабная линейка.
Краткая теория
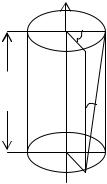
Сдвигом называют такую деформацию твердого тела, при которой все его плоские слои, параллельные некоторой плоскости, называемой плоскостью сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу. Этот вид деформации возникает под действием сил, приложенных к двум диагонально противоположным граням тела, ка-
сательным к той поверхности, на которую они действуют (рис.1). |
|
|||||||
|
|
|
Fτ |
Касательная сила F , действующая |
||||
B |
|
B` |
на единицу |
поверхности, называется |
||||
A |
|
|
тангенциальным (касательным) |
напря- |
||||
Fτ |
|
|
|
жением: |
σ = |
Fτ |
. |
(1) |
0 |
|
|
||||||
|
|
|
||||||
|
|
|
|
|
|
S |
|
|
Рис. 1
65
Измеряется тангенциальное напряжение в тех же единицах, что и давление.
Деформация сдвига характеризуется величиной относительного сдвига . Чтобы объяснить, что такое относительный сдвиг, обратимся к рис. 1. Выберем какие-нибудь точки тела, лежащие на одной прямой, например, точки А и В. При деформации сдвига величины смещения выбранных точек АА и ВВ называются абсолютным сдвигом. Абсолютный сдвиг для различных точек различен (АА ВВ ), но отношение каждого
этого |
сдвига к расстоянию до |
точки О будет одно и то же: |
|||
|
AA′ |
= |
BB′ |
= tgγ . |
|
|
|
|
|
||
|
OA |
OB |
|
||
Если деформации малы, то γ ≈tgγ. |
Поэтому можно сказать, что относи- |
||||
тельный сдвиг есть измеренный в радианах угол сдвига.
По закону Гука для малых деформаций относительный сдвиг про-
порционален тангенциальному напряжению, т. е. |
στ = Gγ . |
(2) |
Величина G называется модулем сдвига. Таким образом, модуль сдвига численно равен тангенциальному напряжению, которое возникло бы в твердом теле при относительном сдвиге, равном единице.
ВСИ модуль сдвига измеряется в Н/м2 (Па), а в системе СГС – в дин/см2.
Вданной лабораторной работе модуль сдвига оп-
|
M |
ределяется косвенно – из деформации кручения. Рас- |
|
0 |
r φ |
смотрим более подробно этот вид деформации и ее |
|
связь с деформацией сдвига. |
|
||
|
|
|
|
L |
γ |
Деформация кручения возникает в |
образце |
(стержне, проволоке и т. п.), если одно сечение образца |
|||
|
|
закреплено неподвижно, а во втором действуют две |
|
|
|
равные по модулю и противоположные поG |
направле- |
|
|
нию касательные силы (пара сил), момент M |
которых |
0` |
B |
относительно центра этого сечения направлен по оси |
|
Рис.2 |
образца (рис. 2). |
|
Под действием крутящего момента M все попе- |
||
|
речные сечения стержня, изображенного на рис. 2, поворачиваются вокруг оси ОО на некоторые углы, тем большие по величине, чем дальше эти сечения расположены от сечения, закрепленного непод-
вижно. Угол поворота верхнего сечения называют углом кручения. В результате деформации кручения возникает перекос на угол образующих цилиндрической поверхности стержня.
По закону Гука угол кручения связан с моментом M соотношением
(3)
где N – модуль кручения, который показывает, какой момент нужно приложить, чтобы закрутить стержень на угол в один радиан. Найдем теперь
66
связь между модулем сдвига и модулем кручения. Для этого предположим, что стержень с радиусом r и длиной L из материала, модуль сдвига которого G, закручен под действием момента M на угол (см. рис. 2). Это означает, что верхнее основание повернуто относительно нижнего на угол .
Вырежем из стержня диск малой высоты dL и положим, что нижнее основание этого диска при закручивании повернулось на угол , а верхнее – на угол + d . Из этого диска вырежем кольцо с внутренним радиусом r и
внешним r + dr (рис. 3а).
Все кубики, вырезанные из такого кольца (рис. 3в), будут иметь одинаковую деформацию сдвига на один и тот же угол . Таким образом, деформация кручения свелась к деформации сдвига. Из рис. 3а видно, что
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γdL = rdϕ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dϕ |
|
|
dL |
dφ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или γ = r |
. (4) |
|||
|
|
|
dL |
|
|
|
γ |
|
|
|
|
dr |
|
|
|
dL |
||||||||
γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим |
теперь |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Рис. 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
упругую |
|
касатель- |
||||||
|
а |
|
б |
|
|
|
|
|
|
|
|
|
|
|
ную силу, |
дейст- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вующую на поверх- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ность кольца, площадь которого dS = 2πrdr . Согласно (1) и (2), |
|
|||||||||||||||||||||||
|
|
|
|
|
dFτ = σ τ dS = G γdS = 2πG γrdr . |
|
|
|
|
|
|
|||||||||||||
С |
другой |
стороны, |
элементарный |
|
|
|
|
момент |
dM |
равен |
||||||||||||||
dM = rdFτ = 2πGγr 2 dr. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Тогда для всего стержня полный момент М равен |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
M |
= r |
= π |
r γ |
r |
2 |
dr |
= |
π |
|
r |
dϕ |
r |
3 |
dr |
. |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
∫ dM |
2 G ∫ |
|
|
2 G ∫ |
dL |
|
|
|
|
|
|||||||||||
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||
После интегрирования получим: M = |
2πG |
dϕ |
|
r 4 |
|
.Очевидно, что для одно- |
||||||||||||||||||
dL |
4 |
|
||||||||||||||||||||||
|
|
|
dϕ |
= ϕ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
родного стержня |
|
Тогда |
|
|
|
M = |
πGϕr 4 |
= |
πGД 4 |
ϕ , |
(5) |
|||||||||||||
|
dL |
|
|
|
|
|||||||||||||||||||
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
2L |
|
|
32 L |
|
|
|
|||
где Д=2r - диаметр стержня.
Подставляя (5) в (3), получим соотношение между модулем круче-
ния N и модулем сдвига G: |
N = |
πGД4 |
. |
(6) |
|
||||
|
|
32L |
|
|
Описание установки и вывод расчетной формулы
Экспериментальная установка состоит из длинной вертикально висящей проволоки, к нижнему концу которой прикреплен горизонтальный металлический стержень с двумя симметрично расположенными грузами (рис. 4). Их положение на стержне можно фиксировать. Верхний конец проволоки зажат в цангу кронштейна и с помощью специального приспо-
67
собления вместе с цангой может поворачиваться вокруг вертикальной оси. Таким образом, в системе можно возбуждать крутильные колебания. К данной системе может быть применен основной закон динамики враща-
|
тельного движения |
|
|
|
|
|
|
|
|
|
|
|
|
M = J |
d 2ϕ |
, |
(7) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dt 2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где М – вращающий момент |
|||
|
1 |
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
относительно оси ОО, J – мо- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мент инерции стержня с гру- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зами относительно той же оси, |
|||
m |
|
|
|
|
|
|
|
|
|
m |
m |
|
|
|
|
|
|
|
|
m |
– угол поворота стержня. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если амплитуда коле- |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
A2 |
A2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
баний невелика, то для опре- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
A1 |
A1 |
|
|
|
|
|
|
|
|
деления момента сил М мож- |
||||||
|
|
|
0` |
|
|
|
|
|
|
|
|
|
|
|
|
но |
воспользоваться |
законом |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
Рис. 4 |
|
|
|
|
|
|
|
|
|
|
|
|
Гука в форме (3). |
Вращаю- |
||
щий момент М в этом случае вызван деформацией проволоки и стремится уменьшить, а не увеличить угол . Поэтому в формуле (3) необходимо переменить знак. Тогда после подстановки (3) формула (7) приобретает вид
|
|
|
|
J = |
d 2ϕ |
= −Nϕ |
или |
d 2ϕ |
+ω2ϕ = 0 , (8) |
|
|
|
|
|
|
|
|||||
|
N |
|
|
dt 2 |
|
dt 2 |
||||
где ω2 = |
. Из уравнения (8) видно, что в рассматриваемом движении ус- |
|||||||||
|
|
|||||||||
|
|
J |
|
|
|
|
|
|
||
корение |
d 2ϕ |
пропорционально смещению и направлено противополож- |
||||||||
dt 2 |
||||||||||
|
|
|
|
|
|
|
|
|||
но ему, а это есть существенный признак гармонического колебательного движения. Решением уравнения (8), как известно, является периодическая функция, изменяющаяся по закону синуса или косинуса.
Таким образом, является циклической частотой крутильных коле-
баний стержня, период которых Т равен |
T = |
2π |
= 2π |
J |
, |
(9) |
|
|
ω |
|
N |
|
|
где J – момент инерции всей системы. Момент инерции крутильного маятника J складывается из момента инерции стержня Jо и момента инерции
двух грузов 2mA2 относительно оси вращения системы. Тогда для двух положений грузов 1–1 и 2–2 (см. рис. 4) имеем:
T = 2π |
Jo + 2mA12 |
и T = 2π |
Jo + 2mA22 |
. |
(10) |
||
|
|
|
|||||
1 |
|
N |
2 |
N |
|
||
|
|
|
|
|
|||
Исключая из этих формул Jo, находим N: |
|
|
|
||||
N = |
|
8π 2 m(A12 |
− A22 ) |
. |
|
|
(11) |
|
|
|
|
|
|||
|
|
T 2 −T 2 |
|
|
|
||
|
1 |
2 |
|
|
|
|
|
Сравнивая (6) и (11), получим формулу для определения модуля сдвига G:
68

G = |
256πLm(A12 − A22 ) |
. |
12) |
|||
Д |
4 |
(T 2 |
−T 2 ) |
|||
|
|
|
1 |
2 |
|
|
Выполнение работы
1.Устанавливают грузы в положения 1–1, приводят систему в крутильные колебания, избегая маятникообразных качаний в сторону, и, пропустив 2–3 колебания, по секундомеру определяют не менее 3-х раз время 30–50 полных колебаний системы, наблюдая прохождение зайчика от зеркальца через вертикальную черту на задней стенке ящика. Число колебаний n указывается преподавателем. Вычисляютпериодколебаний T1 =t1 / n .
2.Переместив грузы в положения 2–2, определяют период колеба-
ний Т2.
3.С помощью микрометра измеряют в нескольких местах диаметр проволоки.
4.Спомощьюлинейкиопределяютрасстояниемеждугрузами 2A1 и 2A2 .
5.Все данные заносят в таблицу и по формуле (2) находят модуль сдвига материала проволоки. Для данной установки L = (131 0,1) см и
m = (270 0,1) г.
№ |
Д, |
n |
2A1 |
, |
t1, |
Т1, |
2A2 , |
t2, |
T2, |
G, |
G, |
G |
100% |
n/n |
мм |
|
мм |
|
c |
с |
мм |
c |
c |
Н/м2 |
Н/м2 |
G |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ср. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольные вопросы
1.Что называется деформацией сдвига? Кручения?
2.Запишите закон Гука для этих видов деформаций.
3.От чего зависит величина модуля сдвига? Единица его измерения?
4.Объясните, как деформацию кручения можно свести к деформации сдвига?
5.От чего зависит период крутильных колебаний?
6.
РАБОТА № 11 ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ
ПО МЕТОДУ СТОКСА
Принадлежности: стеклянный сосуд, наполненный вязкой жидкостью, шарики из свинца, секундомер, измерительный микроскоп, масштабная линейка.
69
Краткая теория
Реальная жидкость, в отличие от идеальной, обладает вязкостью (внутренним трением), обусловленной сцеплением (взаимодействием) между ее молекулами. При движении жидкости между ее слоями возникают силы внутреннего трения, действующие таким образом, чтобы уравнять скорости всех слоев. Природа этих сил заключается в том, что слои, движущиеся с разными скоростями, обмениваются молекулами. Молекулы из более быстрого слоя передают более медленному некоторое количество движения, вследствие чего последний начинает двигаться быстрее. Молекулы из более медленного слоя получают в быстром слое некоторое коли-
чество движения (или импульса), что
Z |
|
|
υ + dυ |
приводит к его торможению. |
|||
|
|
|
|
|
|
Таким образом, при переносе |
|
|
|
S |
|
импульса от слоя к слою происходит |
|||
dZ |
|||||||
|
|
|
|
|
изменение импульса этих слоев (уве- |
||
|
|
|
|
|
|
||
|
|
|
|
|
|
личение или уменьшение). Это зна- |
|
|
|
|
|
υ |
|
||
|
|
|
|
|
|
чит, что на каждый из этих слоев |
|
|
|
|
|
|
|
||
|
|
|
|
|
X |
действует сила, равная изменению |
|
|
|
|
|
|
импульса в единицу времени (второй |
||
Y |
|
Рис. 1 |
закон Ньютона). Эта сила называется |
||||
|
|
|
|
|
силой трения между слоями жидко- |
||
сти, движущимися с различными скоростями (внутреннее трение). Рассмотрим жидкость, движущуюся в направлении оси Х (рис. 1).
Пусть слои жидкости движутся с разными скоростями. На оси Z возьмем две точки, находящиеся на расстоянии dz. Скорости потока отличаются в
этих точках на величину dx. Отношение ddzυ называется градиентом скоро-
сти – векторная величина, численно равная изменению скорости на единицу длины в направлении, перпендикулярном скорости, и направленная в сторону возрастания скорости.
Сила внутреннего трения (вязкости) по Ньютону, действующая между двумя слоями жидкости, пропорциональна площади соприкасающихся
слоев S и градиенту скорости: |
F = –η |
dυ |
S. |
(1) |
|
dz |
|||||
|
|
|
|
Знак минус означает, что импульс движения переносится в направлении уменьшения скорости, η – коэффициент внутреннего трения, или коэффициент вязкости.
Иногда коэффициент вязкости η, определяемый формулой (1), называют коэффициентом динамической вязкости в отличие от кэффициента кинематической вязкости, равного отношению η/ρ, где ρ – плотность жидкости.
Физический смысл коэффициента вязкости η заключается в том, что он численно равен силе внутреннего трения, возникающей на единице
70
