Лекция № 5

Статистические гипотезы и их проверка

Понятие статистической гипотезы

В статистике, как и в жизни, важные утверждения редко удается доказать окончательно и неоспоримо. Можно только выдвинуть утверждение, справедливое с некоторой степенью достоверности.

Статистическая гипотеза - это предположение о виде распределения или о величинах неизвестных параметров генеральной совокупности, которая может быть проверена на основании выборочных показателей.

Примеры статистических гипотез:

Генеральная совокупность распределена по закону Гаусса

(нормальному закону).

Дисперсии двух нормальных совокупностей равны между собой.

Гипотеза «на Марсе есть жизнь» не является статистической,

поскольку в ней не идет речь ни о виде, ни о параметрах распределения.

Вместе с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место альтернативная ей гипотеза. Целесообразно их различать.

Основное проверяемое предположение называется нулевой гипотезой Н0 и обычно формулируется как отсутствие различий, отсутствие влияния фактора, отсутствие различия значения выборочной характеристики от заданной величины (например, нуля) и т. п. Так, если ожидается различие результатов в контрольной и опытной группах, то формулировка нулевой гипотезы звучит так: значения переменной в контрольной и опытной группах неотличимы, т.е. являются выборками из одной и той же генеральной совокупности. Как правило, Н0 не является для исследователя содержательной гипотезой, т. е. предметом и целью доказательства. Другое проверяемое предположение (не всегда строго противоположное или обратное первому) называется конкурирующей или альтернативной гипотезой Н1. Обычно профессиональный интерес исследователя сводится именно к верификации альтернативной гипотезы.

Различают гипотезы, которые содержат только одно и более одного предположений. Гипотезу, содержащую только одно предположение,

называют простой, а гипотезу, которая состоит из конечного или бесконечного числа простых гипотез - сложной.

При сравнении двух выборок могут выдвигаться направленные и ненаправленные гипотезы. Ненаправленная альтернативная гипотеза предполагает, что значения переменной в первой выборке отличны от значений во второй (или отличны от некоторого фиксированного числа).

Направленная альтернативная гипотеза предполагает, что значения переменной в первой выборке больше значений во второй (или фиксированного числа). Направленные и ненаправленные гипотезы проверяются, соответственно, с помощью односторонних и двусторонних

критериев.

Стандартная, но существеннейшая статистическая задача — сравнение значений переменной (или нескольких однотипных переменных) в

нескольких группах (или подгруппах), выбранных из генеральной совокупности согласно некоему условию. Подобные выборки могут быть

независимыми или связанными (сопряженными, парными). Пример

независимых выборок — значение некоторого показателя (например,

артериального давления) в случайным образом сформированных контрольной и экспериментальной группах. Пример связанных выборок — значение показателя (например, артериального давления) у одних и тех же пациентов до и после некоторого воздействия (или воздействий). Сравнение связанных и несвязанных выборок производится с помощью разных критериев.

Ошибки I и II рода

Решение об отклонении или принятии статистической гипотезы принимается по выборочным данным. Поэтому приходится считаться и с возможностью ошибочного решения. Различают ошибки I и II рода.

Ошибка I рода состоит в том, что будет отвергнута правильная гипотеза (т.е. будет отвергнута нулевая гипотеза, в то время, когда она верна).

Ошибка II рода состоит в том, что будет принята неправильная гипотеза (т.е. будет принята нулевая гипотеза, в то время, когда она не верна).

Пороговое значение для принятия отклоняющего решения называется

уровнем значимости и обозначается . Уровень значимости - это вероятность совершить ошибку I рода. Вероятность ошибки II рода обозначают , а величину 1- называют мощностью критерия. Чем больше мощность, тем меньше вероятность ошибки II рода.

Допустимый процент возможных ошибок первого рода - вопрос взаимной договоренности, должны приниматься во внимание возможные последствия принятия ошибочного решения. Ложные решения, например при экспертизе, могут иметь более серьезные последствия, чем ошибочно декларированная чистота химического реактива. Поэтому в первом случае должны быть предусмотрены более высокая достоверность и, следовательно,

более низкое число возможных ошибок I рода, чем во втором случае.

Ошибки I и II рода зависят друг от друга. Чем меньше будет , тем больше будет (и наоборот). Поэтому, нет никакого смысла для проверки значимости выбирать слишком малое значение , так как из-за этого очень вырастает неизвестное . Выбор относится к фазе планирования эксперимента.

Оптимальная величина (критический уровень значимости) должна удовлетворять двум противоречивым требованиям: 1) она должна быть достаточно мала, чтобы обеспечить высокое доверие к выводу об отклонении

Н0; 2) но она должна быть достаточно велика, чтобы реже допускать ошибки

II рода. При этом вероятность ошибки уменьшается при увеличении значения

, а для фиксированного значения : а) при увеличении объема выборки; б)

при уменьшении выборочной дисперсии.

Соотношения вероятностей ошибок. Поясним на наглядном примере соотношения вероятностей ошибок первого и второго рода. Пусть имеется некая большая и нормально распределенная совокупность измерений, характеризующаяся средним значением М1 и какой-то дисперсией. Будем выбирать из этой совокупности случайным образом два подмножества размером в 10 измерений (например, для совокупности из 200

измерений таких различных подмножеств будет 1027). Теперь вычислим для всех пар полученных подмножеств (а они в той или иной степени будут различаться в своих выборочных средних) значения критерия Стьюдента и построим функцию плотности вероятности распределения этих вычисленных значений (рис. 35а, по горизонтальной оси — t-значения). Это и будет распределение вероятностей нулевой гипотезы, когда она верна.

При равенстве средних двух выборок t-значение равно нулю, чем больше разность средних (по модулю), тем больше t-значение (по модулю),

но меньше вероятность такого расхождения. На рис. 35а показано, что только

5% из всех пар выборок имеют разность средних значений, оцениваемых t-

значениями, большими 2,1 (зачерненная область). И только 1% из всех пар выборок имеют разность средних значений, оцениваемых t-значениями,

большими 2,87 (хвостик за второй штриховой линией). Это и будут критические t-значения при =5% и =1% для нулевой гипотезы, когда она верна. То есть при выбранном критическом уровне в проценте случаев нулевая гипотеза будет отвергаться, хотя она и верна (ошибка первого рода).

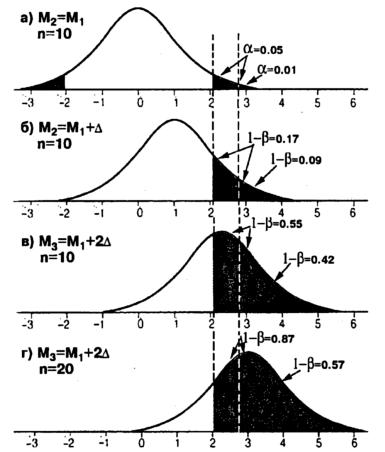
Рис. 35. Соотношения вероятностей ошибок I и II рода.

Пусть теперь имеется другая большая совокупность измерений с такой же дисперсией, но отличающаяся своим средним значением М2 от М1, на некую условную величину . Будем теперь выбирать случайным образом подмножества по 10 элементов из одной и из другой совокупности и сравнивать эти выборки попарно по t-критерию. Полученная в результате функция распределения t-значений будет соответствовать альтернативной гипотезе, когда она верна (при реальной разности средних ). Эта функция,

будет иметь определенное смещение (пусть оно будет такое, как показано на рис. 35б) относительно случая отсутствия различия средних (нулевая гипотеза, рис. 35а).

Как видно из рис. 35б, при выбранном уровне значимости нулевой гипотезы =5 % только для 17 % подмножеств (это чувствительность критерия 1- ) будет принята альтернативная гипотеза различия средних, а

для =84 % случаев будет принята нулевая гипотеза, хотя она не верна

(ошибка второго рода). При снижении же уровня значимости нулевой гипотезы до =1 %, чувствительность критерия к различиям падает до 9 %

подмножеств, а ошибка второго рода соответственно возрастает до 91 %.

Если теперь повторить вышеуказанную процедуру для другой совокупности измерений, которая отличается по своему среднему значению М3 от М1, на величину 2 , то получим функцию распределения t-значений,

еще больше сдвинутую вправо (рис. 35в). Тогда при =5 % уже для 55 %

подмножеств будет принята альтернативная гипотеза, т. е. чувствительность критерия повысится. Если же затем увеличить еще и объем извлекаемых подмножеств вдвое (до 20 элементов) и повторить процедуру, то получим функцию распределения, еще более сдвинутую вправо (рис. 35г), и для =5

% получим чувствительность в 87 % от всех пар сравниваемых подмножеств.

Если же теперь взять другие совокупности, дисперсия которых в два раза меньше рассмотренных, то все функции распределения по сравнению с рис. 35 сожмутся в 1,44 раза относительно своих линий симметрии

(«колокола» уменьшат свой разброс). Критические границы соответственно сдвинутся влево, а зачерненные области принятия альтернативных гипотез расширятся с уменьшением ошибок второго рода.

Аналогичный эффект будет наблюдаться для подмножеств в 10

элементов, если мы применим другой критерий сравнения различий,

обладающий большей чувствительностью.

Такая простая, но трудоемкая процедура извлечения подмножеств из совокупности (метод Монте-Карло) часто используется для табулирования критических значений критериев. Только исходная совокупность в этом случае составляет не 200 элементов, а десятки тысяч. Для многих статистических критериев рассчитаны и построены номограммы (графики зависимостей) чувствительности критерия от объема выборок, уровня значимости и дисперсии, по которым для каждого конкретного случая можно определить вероятность ошибки второго рода.

Критерий значимости. Уровень значимости. Критическая область

Выбор - дело договорное, иногда достаточно выбрать 100 = 10%, в

отдельных случаях практически должна быть исключена возможность ошибочного решения (например, при оценке токсического действия фармацевтического препарата). Тогда проверяемая гипотеза отбрасывается,

как только число возможных ошибок I рода достигает такого пренебрежительно малого уровня, как, например, 100 =0,1%. В

биомедицинской статистике обычно выбирают уровень значимости ,

равный 0,05 или 0,01.

Обычно придерживаются следующих правил.

1.Проверяемая гипотеза отбрасывается, если ошибка I рода может появиться в менее чем 100 =1 % всех случаев (т.е. 0,01). Тогда рассматриваемое различие считается значимым.

2.Проверяемая гипотеза принимается, когда ошибка I рода возможна в более чем 100 =5 % всех случаев ( 0,05). Тогда рассматриваемое различие считается незначимым.

3.Рассматриваемую гипотезу надо обсуждать дальше, если число возможных ошибок I рода лежит в интервале между 5 % и 1 % (0,01 0,05).

Обнаруженная разность интерпретируется как спорная. Часто дополнительные измерения могут прояснить ситуацию. Если по каким-либо причинам дополнительных измерений окажется недостаточно, то полученные данные следует интерпретировать в расчете на самый неблагоприятный случай.

После того, как задались уровнем значимости, находят правило, в

соответствии с которым принимается или отклоняется данная гипотеза.

Такое правило называется статистическим критерием.

Статистический критерий - правило, в соответствии с которым принимается или отклоняется нулевая гипотеза.

Построение критерия заключается в выборе подходящей функции

Т=Т(x1, …, xn) от результатов наблюдений x1, …, xn, которая служит мерой расхождения между опытными и гипотетическими значениями.

Эта функция, являющаяся случайной величиной, называется

статистикой критерия.

Статистика критерия - специально выработанная случайная величина, функция распределения которой известна.

При этом предполагается, что распределение вероятностей Т=Т(x1,…,xn)

может быть вычислено при допущении, что проверяемая гипотеза верна, и

что это распределение не зависит от характеристик гипотетического распределения.

После выбора определенного критерия множество всех возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а

другая - при которых она принимается, т.е. на критическую область и область принятия гипотезы.

Критическая область - совокупность значений критерия, при которых нулевую гипотезу отвергают.

Область принятия гипотезы - совокупность значений критерия, при которых нулевую гипотезу принимают.

Основной принцип проверки гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области -

гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы - гипотезу принимают.

Поскольку критерий Т=Т(x1,…,xn) - одномерная случайная величина,

все ее возможные значения принадлежат некоторому интервалу. Поэтому критическая область и область принятия гипотезы также являются интервалами, и, следовательно, существуют точки, которые их разделяют.

Такие точки называются критическими.

Критические значения критерия - это точки, отделяющие критическую область от области принятия гипотезы.

Различают одностороннюю (правостороннюю или левостороннюю) и

двустороннюю критическую области. Они определяются из следующих выражений:

правосторонняя - Р(Т>Ткр) = ; левосторонняя - Р(Т<Ткр) = ;

двусторонняя - Р(Т<Ткр) + Р(Т>Ткр)= Ткр1< Ткр2.

Критические точки находят по таблицам, соответствующим распределению критерия.

Традиционная трактовка вычисленной значимости Р включает следующие градации:

Р>0,1 — принимается Н0 и делается вывод: «статистически достоверные различия не обнаружены»;

Р<0,1 — неопределенность в отношении Н0 с выводом: «возможны различия на уровне статистической тенденции»;

Р<0,05 — значимое отклонение Н0 с выводом: «обнаружены статистически достоверные различия»;

Р<0,01 — отклонение Н0 с выводом: «различия обнаружены на высоком уровне статистической значимости»;

Критический уровень значимости =0,05 рекомендуется для небольших выборок, когда велика вероятность ошибки II рода. Для больших выборок (более 100 элементов) порог отклонения Н0 полезно снизить до 0,01.

Общая схема проверки гипотез:

1.Исходя из содержания задачи формулируют нулевую и альтернативную гипотезы.

2.Задают величину уровня значимости критерия , т.е. вероятность отвергнуть основную гипотезу, когда она верна.

3.Выбирают некоторую функцию - статистику от результатов наблюдений - и при обеих гипотезах (основной и конкурирующей) находят

законы ее распределения. Это самый сложный этап с теоретической точки

зрения.

4.С помощью закона распределения на основе выбранного уровня значимости область возможных значений статистики разбивают на две или три части (на две части - при односторонней альтернативе, на три - при двусторонней).

5.Делают выборку и по ее результатам вычисляют статистику.

Выясняют, в какую из областей попадает ее значение. Если величина находится в области, где правдоподобна основная гипотеза, то считают, что эксперимент не противоречит основной гипотезе.

Критерии достоверности оценок

В области биометрии применяют два вида статистических критериев:

параметрические, построенные на основании параметров данной совокупности (например, x и sx2) и представляющие функции этих параметров, и непараметрические, представляющие собой функции,

зависящие непосредственно от вариант данной совокупности с их частотами.

Первые служат для проверки гипотез о параметрах совокупностей,

распределяемых по нормальному закону, вторые - для проверки рабочих гипотез независимо от формы распределения совокупностей, из которых взяты сравниваемые выборки. Применение параметрических критериев связано с необходимостью вычисления выборочных характеристик - средней величины и показателей вариации, тогда как при использовании непараметрических критериев такая необходимость отпадает.

При нормальном распределении признака параметрические критерии обладают большей мощностью, чем непараметрические критерии. Они способны с меньшей вероятностью ошибки отвергать нулевую гипотезу, если она не верна. Поэтому во всех случаях, когда сравниваемые выборки взяты из нормально распределяющихся совокупностей, следует отдавать предпочтение параметрическим критериям.