Лекция № 5

В случае очень больших отличий распределений признака от нормального вида следует применять непараметрические критерии, которые в этой ситуации оказываются часто более мощными. В ситуациях, когда варьирующие признаки выражается не числами, а условными знаками,

применение непараметрических критериев оказывается единственно возможным.

Параметрические критерии

Из параметрических критериев в биометрии применяют t-критерий Стьюдента и F-критерий Фишера. Первый используют для сравнительной оценки средних величин, второй - для оценки дисперсий.

t-критерий Стьюдента

Использование формулы Гаусса-Лапласа для сравнительной оценки средних величин затруднено тем, что в качестве аргументов в эту формулу входят генеральные параметры и (которые, как правило, остаются неизвестными), тогда как при обработке и сравнении выборочных групп приходится пользоваться не генеральными, а выборочными характеристиками x и sx2. Учитывая это обстоятельство, английский математик В. Госсет (печатавшийся под псевдонимом Стьюдент), в 1908 г.

параметр заменен на его выборочную характеристику sх, т. е. нашел закон распределения значений:

Оказалось, что отношение разности между выборочной и генеральной средними к ошибке выборочной средней непрерывно распределяется согласно следующей формуле:

где С - константа, зависящая только от числа степеней свободы k=n-1.

Открытый Стьюдентом и теоретически обоснованный Р. Фишером

закон t-распределения служит основой так называемой теории малой выборки, которая характеризует распределение выборочных средних в нормально распределяющейся совокупности в зависимости от объема выборки. t-распределение зависит только от числа степеней свободы k=п-1,

причем с увеличением объема выборки п t-распределение быстро приближается к нормальному с параметрами =0 и =1 и уже при n 30 не отличается от него.

t-распределение симметрично и отражает специфику распределения средней арифметической в случае малой выборки в зависимости от ее объема

(п). Для выборок, объем которых превышает 30 единиц, величина t-

распределяется нормально и не зависит от числа наблюдений. Если же п<30,

характер t-распределения находится в зависимости от числа наблюдений п.

Для практического использования t-распределения составлена специальная таблица, в которой содержатся критические точки (tst) для разных уровней значимости а и чисел степеней свободы k.

Оценка разности средних. Сравнивая друг с другом две независимые выборки, взятые из нормально распределяющихся совокупностей с параметрами 1 и 2, можно предположить, что 1 - 2 = D, а дисперсия этой разности 2D. Значения генеральных параметров неизвестны, однако несложно найти величины выборочных средних и разность между ними

(x1 x2 ) d . Нулевая гипотеза сводится к предположению, что 1= 2.

Критерием для проверки Н0-гипотезы служит отношение

Ошибку средней разности d , обозначаемую символом sd, определяют по формулам:

Если члены генеральной совокупности распределяются нормально, то и разности между ними будут распределяться нормально и случайная величина t=( d -D)/ sd будет иметь распределение Стьюдента с k=п—1 степенями свободы. H0-гипотеза сводится к предположению, что 1 - 2 = D =0. Отсюда t-критерий выразится в виде отношения средней разности к своей ошибке, т.

е.

положительным знаком, это будет свидетельствовать о достоверности разницы. Если же нижняя граница доверительного интервала будет с отрицательным знаком, это будет служить указанием на случайный характер наблюдаемой средней разности.

F-критерий Фишера

Для проверки H0-гипотезы о равенстве генеральных дисперсий

( 21= 22) нормально распределяющихся генеральных совокупностей t-

критерий оказывается недостаточно точным, особенно при оценке разности дисперсий малочисленных выборок. В поисках лучшего критерия Р. Фишер

нашел, что вместо выборочной разности s1–s2 удобнее использовать разность между натуральными логарифмами этих величин, т. е. lns1 - lns2, где s1 s2.

Эта разность, обозначенная Фишером буквой z, распределяется нормально при наличии как больших, так и средних по объему статистических совокупностей.

При определении величины z можно вместо натуральных использовать десятичные логарифмы, так как z=2,3026 (lgs1 - lgs2) или z=2,3026 lg(s1/ s2), а

также z=1,1513 lg(s21/s22), где s21 s22. Д. Снедекор предложил вместо логарифма отношений использовать отношения выборочных дисперсий,

при s21 s22.

Так как принято брать отношение большей дисперсии к меньшей, то критерий F>1. Если s21=s22, то F=1. Чем значительнее неравенство между выборочными дисперсиями, тем больше будет и величина F, и, наоборот, чем меньше окажется разница между дисперсиями, тем меньше будет величина

F.

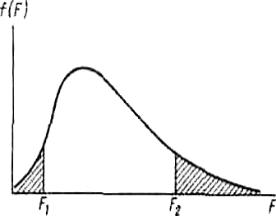
Рис. 36. График плотности вероятности F-распределения для типичных значений степени свободы k1 и k2 и критические границы F1 и F2 (по Н. В.

Смирнову и Дунину-Барковскому, 1965).

Величина F имеет непрерывную функцию распределения и зависит только от чисел степеней свободы k1=п1—1 и k2=n2—1. F полностью

определяется выборочными дисперсиями и не зависит от генеральных параметров, так как предполагают, что сравниваемые выборки,

характеризуемые дисперсиями s21 и s22, взяты из генеральных совокупностей с 21= 22 или из одной и той же генеральной совокупности. Функция распределения возможных значений величины F при небольшом п имеет форму асимметричной кривой, которая по мере увеличения числа испытаний

(п ) приближается к кривой нормального распределения (рис. 36).

Функция F-распределения табулирована для 5 %-го (Р=0,05) и 1 %-го

(Р=0,01) уровней значимости и чисел степеней свободы k1 для большей дисперсии и k2 для меньшей. Если сравниваемые выборки извлечены из одной и той же генеральной совокупности или из разных совокупностей с дисперсиями 21= 22, равными друг другу, то величина F-критерия не превысит критические точки (Fst). Если же выборки взяты из разных совокупностей с их параметрами 21 и 22, не равными друг другу, то Fф Fst

и нулевая гипотеза должна быть отвергнута.

Непараметрические критерии

Правильное применение параметрических критериев для проверки статистических гипотез основано на предположении о нормальном распределении совокупностей, из которых взяты сравниваемые выборки.

Однако это не всегда имеет место, так как не все биологические признаки распределяются нормально. Немаловажным является и то обстоятельство,

что исследователю приходится иметь дело не только с количественными, но и с качественными признаками, многие из которых выражаются порядковыми номерами, индексами и другими условными знаками. В таких случаях необходимо использовать непараметрические критерии.

Для сравнения двух независимых выборок можно рекомендовать W-

критерий Уилкоксона (в качестве нулевой принимается гипотеза о совпадении средних (медианных) значений двух выборок). Более строгие критерии Вальда-Вольфовица и Ван дер Вардена проверяют гипотезы о

совпадении распределений значений в двух выборках. Однако доказано, что критерий Вальда-Вольфовица обладает сравнительно малой чувствительностью.

Ниже рассмотрены некоторые непараметрические критерии,

применяемые для проверки нулевой гипотезы при сравнении как независимых, так и зависимых выборочных групп.

X-критерий Ван-дер-Вардена

Этот критерий относится к группе ранговых критериев, его применяют для проверки нулевой гипотезы при сравнении друг с другом независимых выборок. Техника расчетов X-критерия сводится к следующему.

1.Сравниваемые выборки ранжируют в один общий ряд по возрастающим значениям признака.

2.Затем каждому члену ряда присваивают порядковый номер,

отмечающий его место в общем ранжированном строю.

3. Далее по порядковым номерам одной из выборок, обычно меньшей по объему, находят отношение

где N+1=n1+n2+1, т. е. сумма всех членов сравниваемых групп,

увеличенная на единицу, R—порядковый номер членов ряда, их «ранг».

4.С помощью специальной таблицы находят значения функции[R/(N+1)] для каждого значения R/(N+1).

5.Суммируя результаты (обязательно с учетом знаков!), получают величину Хф= [R/(N+1)], которую сравнивают с критической точкой этого критерия Хst для принятого уровня значимости и общего числа членов сравниваемых выборок, т. е, N=n1+n2.

6.Нулевая гипотеза сводится к предположению, что сравниваемые выборки извлечены из генеральных совокупностей с одинаковыми функциями распределения. Если окажется, что Хф>Хst, нулевая гипотеза должна быть отвергнута на принятом уровне значимости.

Критерий знаков z

Втех случаях, когда результаты наблюдений выражаются не числами,

азнаками плюс (+) и минус (-), различия между попарно связанными членами сравниваемых выборок оценивают с помощью критерия знаков z.

Конструкция этого критерия базируется на весьма простых соображениях:

если попарно сравниваемые значения двух зависимых выборок существенно не отличаются друг от друга, то число плюсовых и минусовых разностей окажется совершенно одинаковым; если же заметно преобладают плюсы или минусы, это будет указывать на положительное или отрицательное действие изучаемого фактора на результативный признак. Большее число однозначных разностей служит в качестве фактически найденной величины z-критерия знаков. При этом нулевые разности, т. е. случаи, не давшие ни положительного, ни отрицательного результата, обозначаемые цифрой 0, в

расчет не принимают и число парных наблюдений соответственно уменьшается.

Как и всякий другой выборочный показатель, z-критерий знаков является величиной случайной; он служит для проверки H0-гипотезы, т. е.

предположения о том, что совокупность или совокупности, из которых взяты сравниваемые выборки, имеют одну и ту же или одинаковые функции распределения. H0-гипотеза отвергается, если zф>zst для принятого уровня значимости и числа парных наблюдений п, взятых без нулевых разностей.