Диференціальне числення ФОЗ
.pdf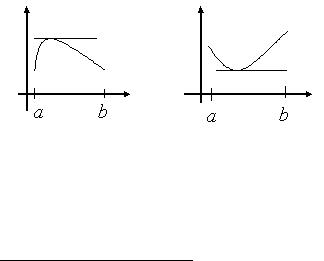
12. & .
# ', * + , " - ' ' 4 , * " *3 ( . & + * -
* – %. 7, /.$', ?.–2.2 + ).3..
! (* ( y = f ( x ) (a,b)
c " " "
$ . ), % c f ′(c ) , f ′(c ) = 0 .
. % " , c " y = f ( x) ! , (! *3 (a,b) ". # x (a, c ) (c,b ) :
f ( x ) < f (c) . . ' x = c |
x , ! c + x - |
||||||||
+ (a,b) . 7 " y = f ( x) , y = |
|||||||||
= f (c + |
x) − f (c ) < 0 . $": |
|
|||||||
f ′(c ) = lim |
f (c + |
x) − f ( x) |
. |
|
|
|
|||
|
|
|
|
|
|||||
|
x→0 |
|
|
|
x |
|
|||
|
|
|
|
|
|
|
|
|
|
8 |
x > 0 , |
y |
< 0 , f ′(c ) ≤ 0 ( ! " |
||||||
|
|||||||||
|
|
|
x |
|
|
|
|
|
|
). " x < 0 , |
y |
> 0 , |
f ′(c ) ≥ 0 . 6 - |
||||||
|
|||||||||
|
|
|
|
|
|
|
x |
|
|
( ,, |
f ′(c ) = 0 . # . |
||||||||
5" , ( ( : " c " - " , (! *3 ! ( 3 (a,b) ", (
, , " * Ox ( . 20 ,
!).
|
! |
$ . 20.
* 7 %’, (1601–1665) – ( * ( . $ ,
, + ! ( ' * ". &-
7.
42
". # + " , , " -
! . . , " y = x "- , (! *3 [0;1] " x = 1, ( ) (
,: y′ = 1. ', '.
! '*. ( y = f ( x )
1)$ [a,b] ,
2)(a,b) ,
3) $ [a,b] " $ , " f (a ) = f (b) .
) (a,b) $ c , % -
f ′(c ) = 0 .
. ) * " y = f ( x ) [a,b] ,
' ' & (, 3 ( . «& ») - " , * ( 3 " m (! *3 -
" M . ), m ≤ f ( x) ≤ M . $" + . 1). m = M . # f ( x ) = const [a,b] , + f ′( x ) = 0 x (a,b ) , !
" c + " ! * " (a,b) .
2). m < M . # f (a ) = f (b) ,, ! *
! , * " " [a,b] . % " ,
" " ", * " M , ! c (a,b) : f (c ) = M . c
" , * " (! *3 " (a,b) , + - ' 7 f ′(c ) = 0 . # .
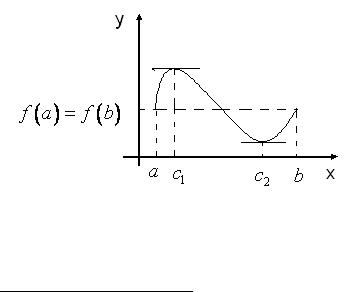
6 " ,, -
(a,b) , ! c , " (
* Ox . . . 21 c1 c2 .
$ . 21.
* $* / 3 * (1652–1719) – * ( . % ' !.
43
6 $" , : " " -
t1 t2 , , * " + ", , ( +
, ! x(t1 ) = x(t2 ) , + (t1 , t2 ) ( * " (
t , " ( , 3 * ! ' ': v(t ) = = x′(t ) = 0 . & ( , ( 3 ".
". & $" ,, ! " -! ! * + " . $"
.
1. & * 3 , ! ' * '. $" [0; 1] ' ( . 22).
x, 0 ≤ x < 1, f (x ) =
0, x = 1.
$ . 22.
" , , , " ( ', ', *
f′( x ) = 1 x (0;1) .
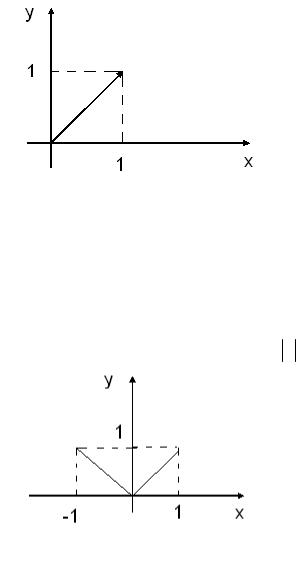
2.& * , 3 3 * 3 '. # " ' f ( x ) = x [−1;1] ( . 23).
$ . 23.
44
6 , c (−1;1) , f ′(c ) = 0 , * f ′( x ) = 1 x (0;1) , f ′( x ) = −1 x (−1;0) , x = 0 , ( . . 3).
3. & * * , 3 3 3 . $"
' y = x [0;1] ( . 24). 0 , " (
' ! ', * f ′( x ) = x′ = 1 x (0;1) .
$ . 24.
6 $" ' * . $ 1. * "
. $ 2. & % $
T , " (kT , (k +1)T ) ( k ) ,
.
! % & "*. & % y = f ( x ) $ [a,b]
(a,b) , (a,b) $ -
c , % : f (b) − f (a ) = f ′(c )(b − a ) .
. & + ' ϕ( x ) = f ( x ) + λx , λ
! , : ϕ(a ) = ϕ(b) . # f (a ) + λa = f (b ) + λb , :
λ = − f (b) − f (a ) . b − a
# " y = ϕ( x ) [a,b] * "
$". (, [a,b], " (,
( (a,b) " ( (, "
[a,b] ( , ". 6 $" c (a,b) ,ϕ′(c) = 0 . * ϕ′( x) = f ′( x) + λ ,
* 2 + ?–2 (1736–1813) – ( * ( , -
( ". 6 ! ( .
45
f ′(c ) = −λ = f (b) − f (a ) , b − a
( ! ! .
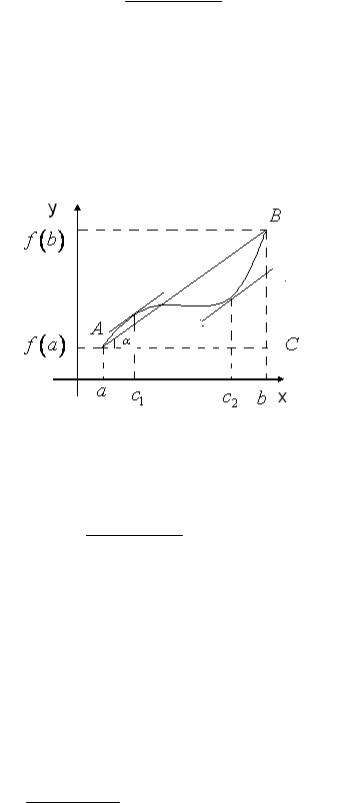
# 2 + , ( ( . $"
y = f (x ) [a,b] ( . 25). % AB . > (
,:
tg α = |
|
|
|
= |
f (b) − f (a ) |
. |
|
|
|
BC |
|
||||
|
|
||||||
|
|
|
|
|
|||
|
|
|
AC |
|
|
b − a |
|
|
|
|
|
|
|
|
|
$ . 25.
6 3 !, *
f ′(c ) = f (b) − f (a ) = tg α , b − a
,, ( , -
, " c , , - , , ! * (. #
2 + ,, -
(a, b) ( * " ( c , " ( , -
, * ( AB . . . 25
– c1 c2 .
# 2 + , + '. 8 x = x(t) (t1 ≤ t ≤ t2 ) – , , * ", 3 "
x (t2 ) − x (t1 )
t2 − t1
, ' 3 * + [t1 ,t2 ] . # 2 +
+ ,, ( * " t* (t1 < t* < t2 ), " ( , 3-
* x′(t* ) ! ' (: 46
x′(t* ) = x (t2 ) − x (t1 ) . t2 − t1
#. " y = x3 − 2x [−1;1] ( , " (
* (.
/ ,: f (a ) = (−1)3 − 2(−1) = 1, |
f (b) = 1 − 2 1 = −1, f ′(x ) = 3x2 − 2 . # |
|||||||||||||||||
' 2 +: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
f ′(c ) = 3c2 − 2 = |
f (b) − f (a ) |
= |
|
−1 −1 |
|
= −1, |
||||||||||||
|
1 − (−1) |
|||||||||||||||||
|
|
|
|
|
|
b − a |
|
|
|
|
|
|
||||||
3c2 = 1; c = ± |
1 |
|
, ! c = − |
1 |
|
, c |
= |
1 |
|
. |
||||||||
|
|
|
|
|
|
|
|
|
||||||||||
3 |
|
|
1 |
|
3 |
2 |
|
3 |
|
|||||||||
|
|
|
|
|
|
|
||||||||||||
# 2 + ( ' * )
! *3.
! ) ** ( y = f (x ), y = g ( x) $
[a,b], (a,b), x (a, b) : g′( x ) ≠ 0 . ) (a,b) $ c ,
% :
f (b) − f (a ) |
= |
f ′(c) |
|
|
|
. |
|
g (b) − g (a ) |
g′(c ) |
||
. 8 2 +, + ':
ϕ( x) = f ( x) + λg (x ) ,
λ ! , : ϕ(a ) = ϕ(b) . #:
f(b) − f (a )
λ= − g (b) − g (a ) ,
+ " y = ϕ( x ) [a,b] * ", $ -
", " ' c (a,b) : ϕ′(c) = 0 . * ϕ′( x) = f ′(x ) + λg′(x ) ,f ′(c ) + λg′(c) = 0 , +:
f ′(c ) f (b) − f (a ) g′(c) = g (b) − g (a ) .
# .
# 2 + , 3 ( g (x ) = x ).
2 + * +, ". / + " + ", 3 -
2 +, : y = f (x ) y = g ( x) [a,b] -
* "' *, , 2 +, :
* 3 ) '–2 (1789–1857) – ( * ( . 6 ! (
, ( (, * " *, !.
47
f (b ) − f (a ) |
= |
f ′(c)(b − a ) |
= |
f ′(c ) |
|
|
|
|
. |
||
g (b ) − g (a ) |
g′(c )(b − a ) |
g′(c) |
|||
. c " + 2 + ", * (
(:
f (b) − f (a ) |
= |
f ′(c1 )(b − a ) |
= |
f ′(c1 ) |
|||
|
|
|
|
|
. |
||
g (b) − g (a ) |
g′(c |
)(b − a ) |
g′(c |
) |
|||
|
|
2 |
|
|
2 |
|
|
3 + , " * c , " ! (. 0 3 ", " + , : 3 ,
g′(x ) ≠ 0 x (a,b ) . 5 , + g′(c) * " +
. + , 3 ( : g (b) − g (a ). : + g (b) − g (a ) ≠ 0 ? 6’" , * ", (. (, " ! -
* * g (a ) = g (b) , " y = g (x) [a, b] -
* " ! $", " ( (a,b) -! c , g′(c ) = 0 , 3: g′( x ) ≠ 0
x (a, b).
" 3 – + , ( 2-
+. " , ! * ", ( " "
y = f ( x) (a ≤ x ≤ b) , , 2 +, -
: x = ϕ(t), y = ψ(t) , α ≤ t ≤ β ; ϕ(α) = a, ϕ(β) = b , f (a) = ψ(α) ,
f (b) = ψ(β) , f ′( x) = ψ′(t)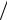
ϕ′(t) . # 2 + ! , ":
|
ψ(β) − ψ(α) |
= |
ψ′(t ) |
|
|
|
|
|
, |
(12.1) |
|
|
ϕ(β) − ϕ(α) |
|
|||
|
|
ϕ′(t ) |
|
||
t – " t , " ψ′(t ) |
ϕ′(t ) = f ′(c) . # ! |
||||
3. 2 (12.1) + , ( -
, , ’, , x = ϕ(t), y = ψ(t) , α ≤ t ≤ β ,
– ( , " ( 3 ( , , " -
, ' t = t .
13. # %.
. 3 + + " !-
" * ( (
! ( %*). ( y = f (x ), y = g ( x) $ -
(a,b) , lim f ( x) = 0 ,
x→ a+0
* 2 * ( 7 (1661–1704) – * ( . & 3 ( - * " « ».
48
lim |
g ( x) = 0 , |
x (a,b) : g′( x) ≠ 0 . ), % |
|||||||
x→ a+0 |
|
|
|
|
|
|
|
|
|
lim |
f ′( x ) |
= K , , lim |
f (x ) |
, ", |
|||||
|
|
||||||||
x→ a+0 g′( x) |
|
|
x→ a+0 g ( x ) |
|
|||||
" |
|
|
|
|
|
|
|
|
|
lim |
f (x ) |
= |
lim |
f ′( x ) |
= K . |
|
|
||
|
|
|
|
||||||
x→ a+0 g ( x ) |
x→ a+0 g′( x) |
|
|
||||||
. |
.( x (a,b) . f ( x) g ( x) |
||||||||
a , ': f (a) = g (a) = 0 . # ,,
f ( x) g ( x) [a, x] . # * "' * -
3, " ( , ξ (a, x) ,
f (x) |
= |
f ( x) − f (a) |
= |
f ′(ξ) |
. |
(13.1) |
|
|
|
||||
g ( x) g ( x) − g (a) g′(ξ) |
|
|||||
8 x → a + 0 , ξ → a + 0 , , lim |
f ′(ξ) |
||||||||
|
|
||||||||
|
|
||||||||
|
|
|
|
|
|
ξ→ a+0 g′(ξ) |
|||
# (13.1) , " lim |
|
f (x) |
= K . |
|
|
|
|
||
|
|
|
|
|
|
||||
|
|
x→ a+0 g (x) |
|
|
|
|
|||
" 1. |
# ! , , x → a − 0 |
||||||||
x → a . |
|
|
|
|
|
|
|
|
|
" 2. |
# , a = + ∞ ! a = − ∞ |
||||||||
lim |
f ( x) = lim g ( x) = 0 , g′( x) ≠ 0 x > x , , |
lim |
f ′( x) |
= K |
|||||
|
|||||||||
x→ + ∞ |
x→ + ∞ |
0 |
|
x→ + ∞ g′( x) |
|||||
|
|
|
|||||||
=K .
,"-
. 0
* , |
lim |
f ( x) |
= K . (, |
|||||||||||||||||||
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x→ + ∞ g ( x) |
|
|
|
|||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
′ |
|
|
|||||||
|
f |
(x ) |
|
f |
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
lim |
= lim |
z |
|
= lim |
|
|
z |
|
= lim |
|||||||||||||
g |
( |
x |
) |
g |
|
|
1 ′ |
|||||||||||||||
x→ + ∞ |
|
|
z→ + 0 1 |
z→ + 0 |
|
|
|
|
|
|
|
|
z→ + 0 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
||||
#. 6 ( ' |
|
lim |
e3 x − e2 x |
. |
||||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→ 0 |
x |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
":
1 |
|
|
|
1 |
|
|
|
|
|||
f ′ |
|
|
|
− |
|
|
|
f ′(x ) |
|
||
|
|
z2 |
|
|
|||||||
z |
|
|
|
|
= lim |
. |
|||||
1 |
|
|
|
1 |
|
||||||
|
|
x→ + ∞ g′( x) |
|||||||||
g′ |
|
|
|
− |
|
|
|
|
|
|
|
|
|
z 2 |
|
|
|
||||||
z |
|
|
|
|
|
|
|
||||
/ , * |
0 |
. 6 , 2 " (!, " +- |
|||||
|
|||||||
|
|
|
0 |
|
|||
+ * , «,»). |
|||||||
|
e3 x − e2 x |
|
3e3 x − 2e2 x |
|
|||
lim |
|
= lim |
|
= 3 − 2 = 1. |
|||
x |
1 |
||||||
x→0 |
x→0 |
|
|
|
|||
|
|
|
|
|
|||
49
" 3. 8 f ′( x ), g′( x) * "' * ,( y = f ( x ), y = g ( x) , 2 " +
. # :
lim |
f ( x ) |
= lim |
f ′( x) |
= lim |
f ′′(x ) |
. |
|
|
|
||||
x→ a g (x ) |
x→ a g′(x ) |
x→ a g′′( x) |
||||
0 , , 2 " + -
, ( " .
#.
|
x − sin x |
|
0 |
|
|
1 − cos x |
|
0 |
|
|
sin x |
|
0 |
|
|
cos x |
|
1 |
|
||
lim |
|
|
= |
|
|
= lim |
|
|
= |
|
|
= lim |
|
= |
|
|
= lim |
|
= |
|
. |
x |
3 |
|
3x |
2 |
|
|
|
6 |
6 |
||||||||||||
x→ 0 |
|
0 |
|
x→ 0 |
|
0 |
|
x→ 0 6x |
0 |
|
x→ 0 |
|
|
||||||||
6 ' 2 " +
∞ .
∞
!. ( |
|
y = f ( x), y = g ( x) $ |
|||||||||
x > x0 , g′( x) ≠ 0 x > x0 , |
lim f (x) = + ∞ , |
lim g (x) = + ∞ . |
|||||||||
|
|
|
|
|
|
|
|
|
x→ x0 |
x→ x0 |
|
), % lim |
|
f ′(x ) |
, lim |
f (x ) |
, : |
||||||
|
|
|
|
||||||||
|
|
x→ x0 g′( x) |
x→ x0 g ( x) |
|
|||||||
lim |
f (x ) |
= lim |
|
f ′(x ) |
. |
|
|
|
|
||
|
|
|
|
|
|
|
|||||
x→ x0 g ( x) |
x→x0 g′( x ) |
|
|
|
|
||||||
" , *. 6 + *, -
' + , * " x0 = + ∞ , x0 = − ∞ , x0 = ∞ .
#.
1. 6 (
|
3x2 |
+ 2x − 1 |
|
lim |
|
|
. |
|
|
||
x→ + ∞ 4x2 |
− 5x + 6 |
||
5' ' + ! ! " 2 " 3 "
" * x2 . % 2 " ( -
,:
|
3x2 + 2x − 1 |
∞ |
|
|
6x + 2 |
∞ |
|
6 |
|
3 |
|
|||||||||
lim |
|
|
|
|
= |
|
|
= |
lim |
|
= |
|
|
= |
lim |
|
= |
|
. |
|
|
2 |
− 5x + 6 |
|
|
|
|
4 |
|||||||||||||
x→ + ∞ 4x |
|
|
∞ |
|
x→ + ∞ 8x − 5 |
|
∞ |
|
x→ + ∞ 8 |
|
|
|||||||||
2. 6 ( lim |
ln x |
|
(α > 0). |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
x→ + ∞ xα |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
/ , * ∞ , 2 " ,:
∞
* " + (, , : ./.7 *. * -
* ", .1. – /.:”. ”, 1969. – .320–321.
50
|
ln x |
|
|
1 |
1 |
|
1 |
|
|
|
|
|
x |
|
|
||||
lim |
|
= |
lim |
= |
|
lim |
|
= 0 . |
|
|
|
|
|
||||||
x→ + ∞ xα |
|
x→ + ∞ αxα−1 |
|
α x→ + ∞ xα |
|
||||
6 * ,, " , * 3, + ! * " " .
3. 6 (
lim xα (α > 0) .
x→ + ∞ ex
6 , * ∞ . 6 , 2 ", -
∞
* . $" .
). α = n . 6 , 2 " n . ) ,:
lim |
xα |
= |
lim |
nxn−1 |
= lim |
n (n − 1) xn−2 |
= ... = |
|||||
|
|
|
|
|
ex |
|||||||
x→ + ∞ ex |
|
x→ + ∞ ex |
|
x→ + ∞ |
|
|||||||
= lim |
n (n − 1)L2 x |
|
= lim |
n! |
= 0 . |
|
||||||
|
|
|
||||||||||
x→ + ∞ |
|
ex |
|
x→ + ∞ ex |
|
|
||||||
!). α . %: n = [α] + 1 ( [α] α ).
# α − n < 0, |
α − n + 1 > 0 . «% ,» n . ) ,: |
|||||||
lim |
xα |
= lim |
αxα−1 |
= L = lim |
α (α − 1)L(α − n + 1) xα−n |
= |
||
|
ex |
|
ex |
|||||
x→ + ∞ ex |
x→ + ∞ |
x→ + ∞ |
|
|
||||
|
|
|
|
1 |
|
|
|
|
= α (α − 1)L(α − n + 1) lim |
|
|
= 0 . |
|
||||
|
|
|
||||||
|
|
|
|
x→ + ∞ xn−αex |
|
|
||
6 * ,, , 3 3, + ! * " -
" .
6 ' 2 " + 3
3 " " ( |
0 |
! |
∞ |
. |
||
|
|
|||||
|
0 |
|
∞ |
|||
#. |
|
|
|
|
|
|
1. lim (2 − x )tg |
πx |
. |
|
|
|
|
4 |
|
|
|
|||
x→ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
# * 0 ∞ . 6 |
0 |
, " |
|||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||
, 2 ": |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
lim (2 − x )tg |
πx |
= lim |
2 − x |
|
= |
0 |
= lim |
|
|
−1 |
|
|
|
|
= |
4 |
lim sin2 |
πx |
= |
4 |
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x→ 2 |
4 x→ 2 |
ctg |
πx |
|
|
0 |
|
x→ 2 |
− |
|
1 |
|
|
|
π |
|
|
π x→ 2 |
4 π |
|
|||||||
|
|
|
4 |
|
|
|
|
|
|
sin |
2 πx |
|
4 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
51