Билет № 1.

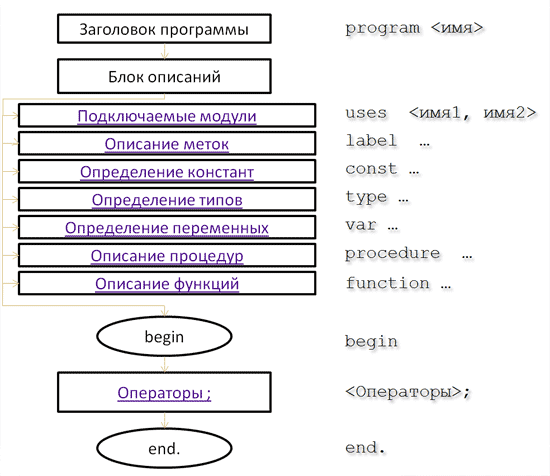
1)

2)Интерполяционный многочлен вида

называется интерполяционным многочленом Лагранжа.  

Интерполяционный многочлен Лагранжа —многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n+1 пар чисел (x₀, y₀), (x₁, y₁),…, (x_n, y_n), где все x_j различны, существует единственный многочлен L(x) степени не более n, для которого L(x_j) = y_j.

l_i(x) обладают следующими свойствами:

• являются многочленами степени n

• l_i(x_i) = 1

• l_i(x_j) = 0 при j ≠ i

Отсюда следует, что L(x), как линейная комбинация l_i(x), может иметь степень не больше n, и L(x_i) = y_i.

Билет № 2

1) Кроме стандартных типов данных Паскаль поддерживает пользовательские типы данных. К ним относятся перечислимые типы (когда непосредственно, в разделе описания типов, заранее записываются все значения для переменных этого типа), интервальные (когда задаются границы диапазона значений для данной переменной) т массивы.Данные этих типов занимают в памяти один байт, поэтому скалярные пользовательские типы не могут содержать более 256 элементов. Их применение значительно улучшает наглядность программы, делает более легким поиск ошибок, экономит память.Перечислимый тип данных задается непосредственно перечислением всех значений, которые может принимать переменная данного типа. При описании отдельные значения указываются через запятую, а весь список заключается в круглые скобки.Интервальный тип позволяет задавать две константы,определяющие границы диапазона значений для каждой переменной.Обе константы должны принадлежать одному и тому же стандартному типу (кроме real).

Массивы - это совокупности однотипных элементов. Характеризуются они следующим:

• каждый компонент массива может быть явно обозначен и к нему имеется прямой доступ;

• число компонент массива определяется при его описании и в дальнейшем не меняется.

2) Квадратурная формула - приближенная формуладля вычисления определенного интеграла.

- формула левых прямоугольников

- формула правых прямоугольников

- формула средних прямоугольников

- метод трапеций

- метод парабол(Симпсона)

Билет № 3

1)Описание переменных выглядит следующим образом – VAR ИмяПеременной1, ИмяПеременной2, ИмяПеременной3: ИмяТипа;

Имя типа может быть именем стандартного типа языка или введенного программистом в предшествующем блоке описания типов TYPE.

Структура процедуры имеет следующий вид:

Procedure <имя процедуры>(формальные параметры : их тип);

Var (локальные переменные)

Begin

end;

Другой вид подпрограммы-функция-оформляется аналогично процедуре. Отличительные особенности функции: она имеет только один результат выполнения (но может иметь несколько входных параметров); результат обозначается именем функции и передаётся в основную программу. Функция оформляется в следующем виде:

Function <имя функции>(формальные параметры: тип): тип значения функции;

Var

. . .

Begin

. . .

End.

2)В паскале существует несколько функций для округления:

* Round- до ближайшего целого

* RoundTo – сколько знаков после запятой * Trunc - в сторону нуля * Ceil - в сторону увеличения * Floor - в сторону уменьшения

Абсолютная погрешность —является оценкой абсолютной ошибки измерения. 

Относительная погрешность — погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или среднему значению измеряемой величины.

При сложении и вычитании абсолютная погрешность результата не превышает суммы абсолютных погрешностей операндов. Поэтому в случае небольшого числа операндов с разной абсолютной погрешностью выбирается операнд с максимальной погрешностью и остальные округляются с сохранением лишнего знака. При сложении чисел с одинаковыми знаками легко показать, что относительная погрешность суммы не превышает наибольшей относительной погрешности операндов. При вычитании же относительная погрешность для результата, близкого к нулю, может оказаться большой. Поэтому при вычислениях желательно избегать вычитания близких величин.

Относительная погрешность произведения и частного не превышает суммы относительных погрешностей операндов, абсолютная же погрешность зависит от значений самих операндов и при делении, например, на число, близкое к нулю, может оказаться большой. Очевидно, что и при этих операциях нет смысла сохранять точность операндов большую, чем точность наименее точного.

Билет № 4

1)Формальные параметры подпрограммы указывают, с какими аргументами следует обращаться к этой подпрограмме (количество аргументов, их последовательность, типы). Они задаются в заголовке подпрограммы в виде списка, разбитого на группы. Разделителем групп является знак точка с запятой (;). В каждую группу  включаются  параметры одного типа, принадлежащие к одной  категории. Бестиповые параметры могут передаваться только по адресу, то есть как параметры-переменные или как параметры-константы. Главной особенностью бестиповых параметров является отсутствие указания типа параметра в заголовке процедуры.procedure MyProc (var Par1, Par2; const Par3, Par4);

Однако следует помнить, что вследствие отсутствия типа, нельзя использовать бестиповые формальные параметры так же, как и типизированные. Перед использованием требуется выполнить приведение формального бестипового параметра к какому-либо типу.Требование всегда описывать тип-массив для передачи параметра-массива затрудняет разработку универсальных процедур. Например, хотелось бы иметь процедуру, которая может находить сумму элементов произвольного массива, а не только массива из 10 элементов типа integer. Для этого в Паскале предусмотрены так называемые открытые массивы.Открытым массивом называется формальный параметр-массив, для которого указан тип элементов, но не указана его длина. Например:

procedure P5(var a: array of integer);

В качестве фактического параметра можно передавать целочисленный массив любой длины. Формальный параметр a при этом будет массивом, индексы которого начинаются с нуля. Максимальный индекс в открытом массиве можно получить с помощью стандартной функции High(a). Длину фактически переданного массива можно таким образом подсчитать как High(a) + 1.

2) По определению предела, для любого (сколь угодно малого) ε, найдется такое N, что при n>N, |xn – x*|< ε. Члены этой последовательности xn называются последовательными приближениями к решению, или итерациями. Наперёд заданное число ε называют точностью метода, а N – это количество итераций, которое необходимо выполнить, чтобы получить решение с точностью ε.

Существует различные методы нахождения приближенного решения, т.е. способы построения последовательности итераций: Метод деления отрезка пополам (дихотомии),Метод простой итерации,Метод Ньютона (метод касательных),Метод хорд.

В методе хорд кривая f(x) заменяется прямой линией – хордой, стягивающей точки (a, f(a)) и (b, f(b)). В зависимости от знака выражения f(a) f ^//(a) метод хорд имеет два варианта.

Пусть f(a)f ^//(a)>0. Тогда x₀=b, точка a будет оставаться неподвижной. Следующее приближение x₁ находим как точку пересечения хорды, соединяющей точки (a, f(a)) и (x₀, f(x₀)) с осью x. Уравнение хорды: Тогда точка пересечения хорды с осью x:

Пусть теперь f(a)f ^//(a)<0. Тогда x₀=a, точка b неподвижна. Проведем хорду, соединяющую точки (b, f(b)) и (x₀, f(x₀)):.

Вычисляем точку пересечения хорды с осью x: 

На следующей итерации в качестве x₀ надо взять вычисленное значение x₁.

Таким образом, имеем следующую последовательность вычислений:

Если f(a) f ^//(a)>0, то x₀=b и 

Если же f(a) f ^//(a)<0, то x₀=a и 

Окончание итерационного цикла в этом методе происходит по условию малости невязки уравнения: |f(x₁)| < ε или 

Билет №5

1. Описание констант и меток. Примеры.

CONST   ИмяКонстанты1 = Значение1;   ИмяКонстанты2 = Значение2; МЕТКИ: Перед любым оператором языка Паскаль можно поставить метку, что позволяет выполнить прямой переход на этот оператор с помощью оператора перехода goto из любого места программы. Формат: label <имя,...>;

2. Приближенное решение нелинейных уравнений. Метод касательных.

Метод Ньютона (метод касательных). Пусть корень  уравнения отделен на отрезке [a, b], причем инепрерывны и сохраняют определенные знаки при. Если на некотором произвольном шагеn найдено приближенное значение корня , то можно уточнить это значение по методу Ньютона. Положим

(1)

где считаем малой величиной. Применяя формулу Тейлора, получим:

Следовательно,

Внеся эту поправку в формулу (1), найдем следующее (по порядку) приближение корня

В качестве простейших условий окончания процедуры уточнения корня рекомендуется выполнение условия

3 . Вычислить интеграл функции на промежутке [0.1, 0.6]c точностью .

uses crt;

var i,n:integer;

a,b,h,x,e,s1,s:real;

bool:Boolean;

function f(x:real):real;

begin

f:=sqr((exp(x)-exp(-x))/2);

end;

begin

clrscr;

write('a='); readln(a);

write('b='); readln(b);

write('n='); readln(n);

repeat

write('Input e : '); readln(e);

bool:=(e>0.00009)and(e<1);

if not bool then writeln('e=[0.0001 .. 0.9] ese raz.');

until bool;

s:=0; {вначале лучше обнулить - для s1}

repeat

s1:=s;

h:=(b-a)/n;

s:=0; x:=a;

for i:=0 to n-1 do {вычисляем значение функции на отрезке от х0 до хn-1}

begin

s:=s+f(x); {не в данном, а в общем случае надо s+abs(f(x))}

x:=x+h;

end;

s:=h*s; {вычисляем значение интеграла по методу левых прямоугольников}

n:=n*2;

until abs(s1-s)<e;

writeln('I= ',s:2:5, 'N= ',n/2);

readln;

end.

Билет №6

1. Описание операций, их классификация и приоритет.

2. Решение задачи Коши. Метод Эйлера.

Если задачу об отыскании решений дифференциального уравнения удаётся свести к конечному числу алгебраических операций, операций дифференцирования и интегрирования известных функций, то говорят, что дифференциальное уравнение интегрируется в квадратурах.

В приложениях крайне редко встречаются уравнения. интегрируемые в квадратурах. Для исследования и решения уравнений, которые не интегрируются в квадратурах, используются численные методы решения задачи Коши.

 

Численное решение задачи Коши y' = f(x, y), y(a) = y₀ на отрезке [a, b] состоит в построении таблицы приближённых значений y₀, y₁, ..., y_i, ...,y_N решения y = y(x), y(x_i) ≈ y_i ,

в узлах сетки a = x₀< x₁< ...< x_i< ...< x_N = b. Если x_i = a + ih, h = (b-a)/N, то сетка называется равномерной.

 

Численный метод решения задачи Коши называется одношаговым, если для вычисления решения в точке x₀ + h используется информация о решении только в точке x₀.

Простейший одношаговый метод численного решения задачи Коши — метод Эйлера.  В методе Эйлера величины y_i вычисляются по формуле :

y_i+1 = y_{i + h·f(xi, yi):}

y' = f(x, y),  y(a) = y₀ , x ∈ [a, b],

x_i = a + ih, h = (b-a)/N, i = 0,1 , 2, ..., N,  

y(x_i)≈ y_i ,

y_i+1 = y_i + h·f(x_i, y_i).

Для погрешности метода Эйлера на одном шаге справедлива оценка

а для оценки погрешности решения на всём отрезке [a, b] справедливо

Для практической оценки погрешности можно рекомендовать правило Рунге:производятся вычисления с шагом h — вычисляютcя значения y^(h)_i, затем производятся вычисления с половинным шагом h/2 — вычисляютcя значения y^(h/2)_i .

 За оценку погрешности вычислений с шагом h/2 принимают величину

 Если соединить точки (x_i, y_i) прямолинейными отрезками, получим ломаную Эйлера — ломаную линию, каждое звено которой с началом в точке (x_i, y_i) имеет угловой коэффициент, равный f(x_i, y_i).