Интеграл Якоби

Уравнения движения тела Р в форме [9] имеют интеграл, названный интегралом Якоби.

Если уравнения системы [9] умножить соответственно на и сложить, то

Полученное уравнение может быть проинтегрировано, так как силовая функция U зависит только от координат x, y, z и явно от времени не зависит . {1} Выражение в скобках справа представляет собой полную производную. Получим

, где С – постоянная интегрирования.

[10]

Здесь V – скорость тела Р бесконечно малой массы во вращающейся системе отсчета. Выражение [10] называется интегралом Якоби. Он был открыт Якоби в 1836 году. Применение его к выяснению свойств движения тела Р было указано значительно позднее Хиллом.

Смысл интеграла Якоби в том, что скорость тела бесконечно малой массы зависит только от координат и от расстояния до тел конечной массы. {2}

Этот интеграл применяется строго в замкнутой системе 3-х тел, одно из которых, бесконечно малой массы. {3}

Чтобы решить задачу полностью, надо найти еще 5 интегралов. Брунс доказал, что при употреблении прямоугольных координат не существует никаких новых алгебраических интегралов, а Пуанкаре показал, что при употреблении в качестве переменных элементов нет также новых однозначных трансцендентных интегралов.

ВОПРОСЫ.

1. При выводе интеграла Якоби из системы уравнений движения путем суммирования получают уравнение и интегрируют его. Почему это возможно?

2. В чем смысл интеграла Якоби?

3. Где применяется интеграл Якоби?

Поверхности Хилла (поверхности нулевой скорости)

Уравнение [10] дает соотношение между квадратом скорости и координатами тела Р относительно вращающихся осей. Поэтому, если постоянная интегрирования С определена численно начальными условиями, то уравнение [10] определяет скорость, с которой движется бесконечно малое тело во всех точках вращающегося пространства. Обратно, для данной скорости уравнение [10] дает геометрическое место точек относительного пространства, в которых может находиться бесконечно малое тело. {1}

В частности, если скорость V в этом уравнении положить равной нулю, то оно определит поверхности, на которых скорость будет равна нулю. {2} С одной стороны от этих поверхностей скорость будет действительна, а с другой – мнима (так как V² имеет разные знаки). {3}

[11]

Действительно, последнее слагаемое справа постоянное и отрицательное, а первые три слагаемых справа переменны и положительны. Если V²=0, то по разные стороны от этой поверхности V² будет иметь противоположные знаки.

Другими словами, тело Р может двигаться с одной стороны поверхности и не может двигаться с другой, где V²<0.

Несмотря на то, что вообще невозможно сказать какой будет орбита, все же это деление относительного пространства покажет, в каких частях бесконечно малое тело может двигаться и в каких частях не может в соответствии с выбранным значением постоянной С.

Поверхность Хилла – это поверхность раздела областей возможного и невозможного движений тела бесконечно малой массы. {4} Никакой другой информации о траектории движения интеграл Якоби не дает. {5}

Уравнение поверхностей нулевой относительной скорости имеет вид:

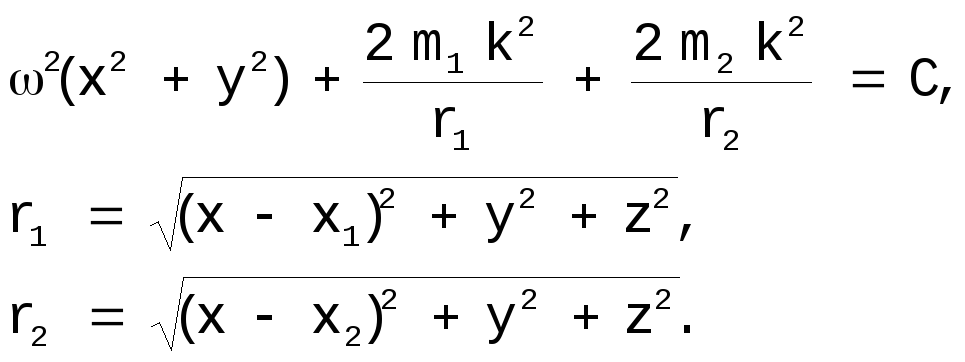[12]

Изучим формы поверхностей нулевой скорости при различных значениях С.

Так как в [12] входят только квадраты координат y и z, то поверхности нулевой скорости симметричны относительно плоскостей y=0 (xz) и z=0 (xy) {в [12] можно заменить y на -y, z на -z, не нарушая равенства}. Если массы тел S и J равны (m₁ = m₂), то поверхности симметричны и относительно плоскости x=0 (yz).

Предположим сначала, что С очень большое число С=С₁. В этом случае поверхность [12] состоит из трех отдельных поверхностей. В самом деле, левая часть уравнения может быть очень большой только в точках, в которых хотя бы один из трех членов этой части принимает очень большие значения.

В точках, где очень велико, второе и третье слагаемые очень малы, так что уравнение можно записать так:

, [13]

где  очень малая по сравнению с С₁ положительная величина.

Таким образом, поверхность [13] (назовем ее асимптотическим цилиндром) лежит внутри цилиндра и асимптотически к нему приближается.

Если r₁ близко к нулю, то первое и третье слагаемое очень малы. Уравнение [12] принимает, следовательно, вид

, [14]

где и очень мало по сравнению с С₁.

Уравнение [14] представляет замкнутую поверхность, заключающую точку S. При эта поверхность в пределе обращается в сферу бесконечно малого радиуса с центром в S (назовем ее квазисферой). Легко видеть, что квазисфера [14] целиком заключает внутри себя сферу , причем больше всего она удаляется от этой сферы в плоскости xy {z=0, поэтому вклад первого слагаемого в максимальный}, а особенно – по направлению к точке J {r₁ минимально, поэтому вклад третьего слагаемого в максимальный}. Квазисфера имеет, таким образом, грушевидную форму.

Третью часть поверхности нулевой скорости образует аналогичная квазисфера

, [15]

окружающая точку J и вытянутая по направлению к точке S.

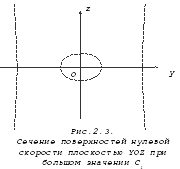
На рисунках 2.1, 2.2 и 2.3 представлены сечения координатными плоскостями поверхностей нулевой скорости в рассмотренном случае, когда постоянная Якоби С=С₁ очень велика. Область невозможного движения расположена внутри асимптотического цилиндра, но вне квазисфер.

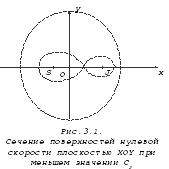
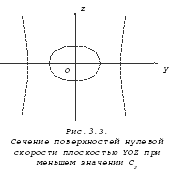
На рисунках 3.1, 3.2 и 3.3 показаны сечения поверхностей нулевой скорости для значения постоянной С=С₂, при котором появляется общая точка у квазисфер. Дальнейшее уменьшение С приводит к слиянию квазисфер и образованию поверхности, имеющей форму гантели, с узкой перемычкой, через которую тело Р может перейти из окрестностей одного тела конечной массы в окрестности другого.

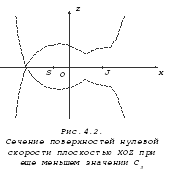
На рисунках 4.1, 4.2 и 4.3 показаны сечения поверхностей нулевой скорости для значения постоянной С=С₃, при котором появляется общая точка у одной из квазисфер и асимптотического цилиндра.

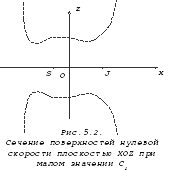
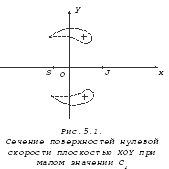
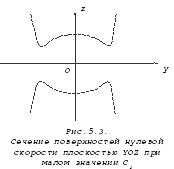
На рисунках 5.1, 5.2 и 5.3 показаны сечения поверхностей нулевой скорости для малого значения постоянной С=С₄, при котором рассматриваемые поверхности обратились в одну двуполостную. При дальнейшем уменьшении С полости этой поверхности уходят на бесконечность. Область невозможного движения сократилась до двух небольших несвязных областей.

Те точки пространства OXYZ, в которых начинается слияние отдельных частей поверхностей нулевой скорости, являются, очевидно, особыми точками этих поверхностей.

Поверхности [12] разделяют области возможного и невозможного движений. Вне асимптотического цилиндра [13] и внутри квазисфер [14] и [15] имеем V²>0 {см. [11] -}, а потому движение возможно. Более того, если в начальный момент времени тело Р находится внутри одной из квазисфер, то оно всегда остается там, поскольку не может пересечь поверхность нулевой скорости; аналогично, если в начальный момент времени тело Р находится вне асимптотического цилиндра, то оно никогда не проникнет к телам S и J.

При уменьшении С область возможных движений будет расширяться {6} и при достаточно малых значениях С она будет заключать всю плоскость xy. Так при С=С₄ движения будут невозможны на плоскости xy лишь внутри небольших областей, ограниченных кривыми, которые при дальнейшем уменьшении С будут сжиматься, обратятся в точки (указанные на рис.5.1 крестиками – это тоже особые точки), а затем совсем исчезнут. После этого поверхность нулевой скорости разделится на две не имеющие общих точек части, одна из которых будет находиться выше плоскости xy, а другая – ниже.

Все вышеизложенное было впервые получено Хиллом и применено к движению Луны. Если, пренебрегая эксцентриситетом орбиты Земли, считать, что движение Луны (тело Р) удовлетворяет уравнениям ограниченной задачи 3-х тел, то ему соответствует значение постоянной Якоби, принадлежащее замкнутой кривой с максимальным расстоянием от центра Земли, равным 109.7 экваториального радиуса. Хилл сделал следующий вывод: «Таким образом, если пренебречь эксцентриситетом земной орбиты, мы имеем строгое доказательство существования верхнего предела радиус-вектора Луны». {7}

ВОПРОСЫ.

1. Верно ли утверждение, обратное интегралу Якоби?

2. Как определяется поверхность нулевой скорости?

3. Может ли тело Р пересечь поверхность нулевой скорости и почему?

4. Что такое поверхность Хилла?

5. Что говорит о траектории движения тела бесконечно малой массы интеграл Якоби?

6. С уменьшением константы Якоби область возможных движений тела бесконечно малой массы расширяется или сужается?

7. Каким образом Хилл обосновал существование верхнего предела радиус-вектора Луны?