Тема 5. Производная и дифференциал

[2] гл. IX, § 1—5; [3] № 907, 908, 910;

[2] гл. X; [3] № 850, 857, 875, 888, 945, 956

[2] гл. XII; [3] № 1067, 1075, 1077.

Разберите решение задачи 8 данного пособия.

Задача 8. Найдите производные функции:

а) у=In (2+sin 3х) ; б) у=(3+1);

в) cos (ху)-3у

Решение: а) Последовательно применяя правило диф­ференцирования сложной функции, правила и формулы диф­ференцирования, имеем:

у'='='='+(sin3х)'='=;

б)у'= '=4(3+1)*(3+1)'=4(3+1)*3*In3*(arctg)'=

=4(3+1)* 3*In3**'=*3*(3+1);

в) В данном случае функциональная зависимость задана в неявном виде. Для нахождения производной у' нужно продифференцировать по переменной х обе части уравнения, считая при этом у функцией от х, а затем полученное урав­нение разрешить относительно у':

-sin (ху)*(ху)'-6уу'+4=0,

-sin (ху)*(у+2хуу')-6уу'+4=0,

-уsin (ху)-2хуу'sin (ху)-6уу'+4=0.

Из последнего уравнения находим у':

2уу'хsin (ху)+3=4- уsin (ху),

у'=.

Вопросы для самопроверки

1. Что называется производной функции?

2. Каков геометрический, физический смысл производ­ной?

3. Как взаимосвязаны непрерывность функции и ее дифференцируемость в точке?

4. Напишите основные правила дифференцирования функций.

5. Напишите формулы дифференцирования основных эле­ментарных функций.

6. Сформулируйте правило дифференцирования сложной функции.

7. Что называется дифференциалом функции?

8. Каков геометрический смысл дифференциала функ­ции.

9. Перечислите основные свойства дифференциала функ­ции.

10. Напишите формулу, позволяющую находить прибли­женное значение функции при помощи ее дифференциала.

11. Как найти производную второго, третьего, n-го поряд­ков?

12. Как найти дифференциал второго порядка от данной функции?

Тема 6. Приложения производной

[2] гл. XI, § 1—3, 7—10; [3] № 1162, 1167, 1201, 1222, 1229.

Разберите решение задач 9, 10 данного пособия.

Задача 9. Исследовать функцию у = и построить ее график.

Решение. Исследование функции проведем по следую­щей схеме:

1. Найдем область определения функции.

2. Исследуем функцию на непрерывность.

3. Установим, является ли данная функция четной, нечет­ной.

4. Найдем интервалы возрастания и убывания функции и точки экстремума.

5. Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба.

6. Найдем асимптоты кривой.

Реализуем указанную схему

1. Функция определена при всех значениях аргумента х, кроме х=1.

2. Данная функция является элементарной, поэтому она непрерывна на своей области определения, т. е. на интерва­лах (—оо; 1) и (1; оо).

В точке х=1 функция терпит разрыв второго рода.

3. Для установления четности или нечетности функции проверим выполнимость равенств f (-х)= f (х) (тогда f(х)— четная функция) или f (-х)= -f (х) (для нечетной функции) для любых х и —х из области определения функции:

f (-х)=, -f (х)=- .

Следовательно, f (-х)f (х) и f (-х) -f (х) , то есть данная функция не является ни четной, ни нечетной.

4. Для исследования функции на экстремум найдем ее первую производную:

у'==-.

у'=0 при х=0 и у' — не существует при х=1. Тем самым имеем две критические точки: х=0, х=1. Но точка х₂=1 не принадлежит области определения функции, экстремума в ней быть не может.

Разобьем числовую ось на три интервала (рис. 5):

(-оо; 0), (0; 1), (1; оо).

В первом и третьем интервалах первая производная отри­цательна, следовательно, здесь функция убывает; во втором интервале—положительна и данная функция возрастает. При переходе через точку х=0 первая производная меняет свой знак с минуса на плюс, поэтому в этой точке функция имеет минимум: у=у(0)=-1. Значит (0;-1) – точка минимума.

На рис. 5 знаками +, — указаны интервалы знакопостоянства производной у', а стрелками — возрастание и убыва­ние исследуемой функции.

4. Для определения точек перегиба графика функции и ин­тервалов выпуклости и вогнутости кривой найдем вторую про­изводную:

у''=-=.

у''=0 при х=-и у'' – не существует при х=1. Разобьем числовую ось на три интервала (рис. 6); (-; -), (-;1), (1;).На первом интервале вторая производнаяу''отрицательна и дуга исследуемой кривой выпукла; на вто­ром и третьем интервалах у">0, тем самым график является вогнутым. При переходе через точку х=-у'' меняет свой знак, поэтому х=-- абсцисса точки перегиба.

Следовательно, В — точка перегиба графика функции.

6. х=1 – точка разрыва функции, причем .

Поэтому прямая х=1 является вертикальной асимптотой графика. Для определения уравнения наклонной асимптоты у=Rх+b воспользуемся формулами:

R=,b= .

Тогда R=,b=;

R=,

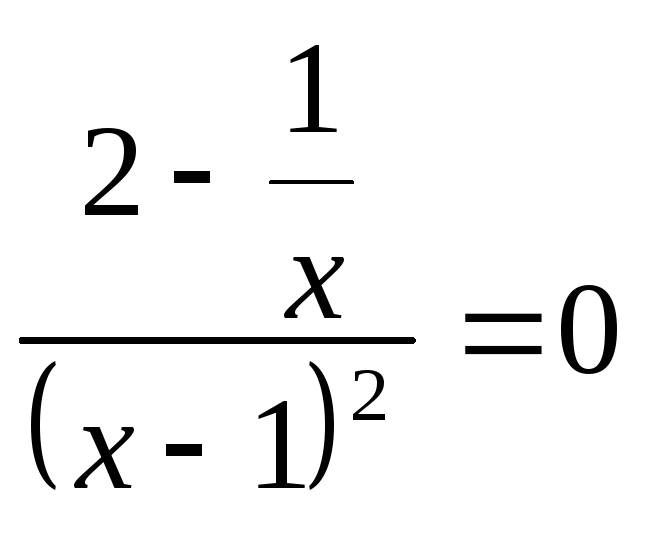b==.

При вычислении последнего предела использовалось правило Лопиталя.

Значит прямая у=0 есть горизонтальная асимптота графика исследуемой функции, представленного на рис. 7.

Задача 10. Резервуар, имеющий форму открытого сверху прямоугольного параллелепипеда с квадратным дном, нужно вылудить внутри оловом. Каковы должны быть размеры ре­зервуара при его емкости 108 л воды, чтобы затраты на его лужение были наименьшими?

Решение. Затраты на покрытие резервуара оловом бу­дут наименьшими, если при данной вместимости его поверх­ность будет минимальной.

Обозначим через а— сторону основания,b—высоту резервуара. Тогда площадьS его поверхности равна а²+4аb, а объем V=а²b²= 108. Отсюда

b= и S= а²+4аb= а²+.

Полученное соотношение устанавливает зависимость меж­ду площадью поверхности резервуара S (функция) и сторо­ной основания а (аргумент). Исследуем функцию S на экст­ремум. Найдем первую производную S', приравняем ее к ну­лю и решим полученное уравнение:

S'=2a-/

Отсюда а = 6. S'(а)>0 при а>6, S' (а)<0 при а<6. Следо­вательно, при а = 6 функция S имеет минимум. Если а=6, то b=3. Таким образом, затраты на лужение резервуара ем­костью 108 л будут наименьшими, если он имеет размеры бдмб дмЗ дм.