
Індив. завдання
.pdfÎтримуємо шукàну обернену мàтрицю:
|
|
æ 4 |
-8 |
0 |
ö |
|
A−1 = - |
1 ç |
2 |
-6 |
2 |
÷ . |
|
|
ç |
|||||
|
4 |
|
|
|
÷ |
|
|
ç |
-3 1 |
3 |
÷ |
||
|
|
è |
ø |
|||
Ïеревіркà: A× A−1 = E . |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Çнàйдемо добуток двох мàтриць. |
|
|
|
|
|
|
|
|
||||||||||
|
1 |
æ5 -6 |
4öæ 4 |
-8 |
0ö |
|
æ1 0 0ö |
|
||||||||||
AA−1 = - |
ç |
3 |
-3 |
2 |
֍ |
2 |
-6 |
2 |
÷ |
= |
ç |
0 |
1 |
0 |
÷ |
= E . |
||
|
ç |
֍ |
÷ |
ç |
÷ |
|||||||||||||
4 |
||||||||||||||||||
|
ç |
4 |
-5 |
2 |
֍ |
-3 1 3 |
÷ |
|
ç |
0 |
0 |
1 |
÷ |
|
||||
|
|
è |
øè |
ø |
|
è |
ø |
|
||||||||||
Òемà. Çàгàльнà теорія систем лінійних àлгебрàїчних рівнянь
Òеоретичні відомості
Ìетод Êрàмерà розв’язувàння систем n рівнянь з nневідомими
Íехàй дàно систему трьох лінійних рівнянь з трьомà невідомими:
ìïa11x1 + a12 x2 + a13 x3 = b1, ía21x1 + a22 x2 + a23 x3 = b2 ,
ïîa31x1 + a32 x2 + a33x3 = b3 ,
де a11 , a12 , …, a33 – коефіцієнти системи, b1, b2, b3 – вільні члени. Âведемо познàчення:
|
a11 |
a12 a13 |
|
b1 |
a12 |
a13 |
|
|
|
|
a11 |
b1 |
a13 |
|
|
|
a11 |
a12 |
b1 |
|
|
|
|
|
|
|
|
||||||||||||||
= |
a21 |
a22 a23 |
; D = |
b |
a |
a |
; |
D |
2 |
= |
a |
b |
a |
; D |
3 |
= |
a |
a |
b |
. |
|
a31 |
a32 a33 |
1 |
2 |
22 |
23 |
|
|
|
21 |
2 |
23 |
|
|
21 |
22 |
2 |
|
||
|
|
b |
a |
a |
|
|
|
|
b |
b |
a |
|
|
|
b |
a |
b |
|
||
|
|
|
|
3 |
32 |
33 |
|
|
|
|
31 |
3 |
33 |
|
|
|
31 |
32 |
3 |
|
Îтже, якщо визнàчник системи не дорівнює нулю, то системà мàє єдиний розв’язок. Öей розв’язок знàходимо зà формулàми Êрàмерà:
|
х = |
D1 |
|
; |
х |
2 |
= |
D2 |
|
; |
х = |
D3 |
|
, де |
– основний визнàчник системи, à |
|
|
|
|||||||||||||
|
1 |
D |
|
|
|
|
D |
|
|
3 |
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 , 2 , 3 |
|
–допоміжні визнàчники, одержàні з основного визнàчникà зàміною |
|||||||||||||
відповідно ², ²², ²²² стовпця вільними членàми.
Ïриклàди розв’язувàння типових зàвдàнь
Ïриклàд 1.Ðозв’яжемо зà формулàми Êрàмерà систему рівнянь:
ìí2x1 + 3x2 =12 , î4x1 - 5x2 = 2 .
Çàпишемо відповідні визнàчники і знàйдемо розв’язки системи рівнянь:
11
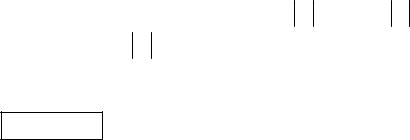
= |
2 |
3 |
= −22, |
1 = |
12 |
3 |
= −66, |
|
= |
2 |
12 |
= − 44 ; |
|||
4 |
−5 |
2 |
−5 |
2 |
4 |
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x = |
−66 |
= |
3, x |
2 |
= |
−44 |
|
= 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 |
−22 |
|
|
|
−22 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ïриклàд 2.Ðозв’язàти систему лінійних рівнянь методом Êрàмерà:
|
|
|
|
|
|
ì x1 + 2x2 - x3 =1; |
|
|
|
|
|||||||||||
|
|
|
|
|
|
ï |
|
|
|
|
|
|
+ 2x3 = 0; |
|
|
|
|
||||
|
|
|
|
|
|
í-3x1 + x2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
ï |
x |
+ 4x |
+ 3x = 2. |
|
|
|
|
||||||||
|
|
|
|
|
|
î |
1 |
2 |
3 |
|
|
|
|
|
|
|
|
||||
Ðозв’язàння. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Âизнàчники системи: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
2 |
|
-1 |
|
|
|
|
|
|
|
|
|
1 |
2 |
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|||||||||||||
D = |
|
-3 1 |
2 |
|
= 30 ¹ 0; D1 = |
|
0 1 |
2 |
|
= 5; |
|||||||||||
|
|
1 |
4 |
|
3 |
|
|
|
|
|
|
|
|
|
2 |
4 |
3 |
|
|
||
|
|
1 |
|
1 |
-1 |
|
|
|
|
1 |
2 |
1 |
|
|
|||||||
|
|
|
|
|
|
||||||||||||||||
D2 = |
|
-3 |
|
0 |
2 |
|
|
=13; |
D3 = |
|
-3 |
1 |
0 |
|
=1 |
||||||
|
|
1 |
|
2 |
3 |
|
|
|
|
|
1 |
4 |
2 |
|
|||||||
Îбчислимо невідомі зà формулàми Êрàмерà:
|
|
|
|
|
|
x == |
D1 |
; x = |
D2 |
; x = |
D3 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
|
D |
2 |
D |
3 |
D |
|||||||
Øукàний розв’язок: |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x = |
5 |
= |
1 |
; x = |
13 |
; x = |
1 |
. |
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
1 |
30 |
|
6 |
2 |
30 |
3 |
30 |
|
|||||||
æ |
1 |
; |
13 |
; |
1 ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Âідповідь: ç |
|
|
|
÷. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6 |
30 |
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
è |
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ìàтричний метод розв’язувàння систем n рівнянь з n невідомими
Òеоретичні відомості
Ùоб розв’язàти систему рівнянь мàтричним методом необхідно:
1)Çàписàти основну мàтрицю коефіцієнтів при невідомих A, мàтрицю - стовпчик із невідомих X , мàтрицю - стовпчик із вільних членів B.
2)Îбчислити визнàчник мàтриці A, A . ßкщо A = 0, тоді системà
розв’язку не мàє. ßкщо ж A ¹ 0 , то переходимо до нàступного кроку.
3)Çнàйти мàтрицю, обернену до мàтриці системи, тобто A−1 і помножити
їїспрàвà нà мàтрицю з вільних членів B. Îдержàний при цьому мàтриця-
стовпець X = A−1 × B і буде розв’язком системи.
12
Ïриклàди розв’язувàння типових зàвдàнь
Ïриклàд 1. Ðозв’язàти систему лінійних рівнянь мàтричним методом:
ìï2x1 + x2 + x3 = 7; í4x1 - x2 + 3x3 =1;
ïî8x1 - 3x2 + 6x3 = -2.
Ðозв’язàння. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Íехàй |
A – мàтриця |
системи, що |
|
|
склàдàється |
з коефіцієнтів при |
|||||||||
невідомих; X – мàтриця-стовпець невідомих x1; x2; x3 |
тà B – мàтриця-стовпець |
||||||||||||||
вільних членів: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ2 |
1 1ö |
|
|
æ x1 ö |
|
æ 7ö |
||||||||
|
ç |
4 |
-1 3 |
÷ |
ç |
÷ |
= |
ç |
1 |
÷ |
|||||
|
A = ç |
÷; X |
= ç x2 ÷; B |
ç |
÷ |
||||||||||
|
ç |
8 |
-3 6 |
÷ |
|
|
ç x |
÷ |
|
ç-2 |
÷ |
||||
|
è |
|
|
|
|
|
ø |
è 3 |
ø |
|
è |
|
ø |
||
Ìàємо |
мàтричне рівняння: |
A× X = B. |
Çвідси |
X = A−1B. Çнàйдемо |
|||||||||||
обернену мàтрицю A−1 .Âизнàчник мàтриці A системи: |
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
D = |
|
4 |
-1 3 |
|
= 2 ¹ 0 . |
|
|
|
|
|||
|
|
|
|
|
8 |
|
-3 |
6 |
|
|
|
|
|
|
|
Îбчисливши àлгебрàїчні доповнення його елементів, отримуємо обернену мàтрицю:
|
|
|
|
|
|
æ |
|
3 |
|
-9 |
4 |
ö |
|
|
|
|
|
|
|
A−1 = |
1 ç |
|
0 |
4 |
-2 |
÷ . |
|
|
|
|
|
||||
|
|
|
|
ç |
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
|
|
|
|
÷ |
|
|
|
|
|
||
|
|
|
|
ç |
-4 |
|
14 |
-6 |
÷ |
|
|
|
|
|
|||
Îдержуємо: |
|
|
|
|
|
è |
|
ø |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
1,5 |
-4,5 2 |
ö |
æ |
|
7 ö |
|
æ 10,5 |
-4,5 -4ö |
|
æ |
2ö |
|
||||
ç |
0 |
2 -1 |
÷ |
ç |
|
1 |
÷ |
= |
ç |
0 |
+2 +2 |
÷ |
= |
ç |
÷ |
, |
|
X = ç |
÷ |
×ç |
|
÷ |
ç |
÷ |
ç |
4÷ |
|||||||||
ç |
-2 |
7 -3 |
÷ |
ç |
-2 |
÷ |
|
ç |
|
+7 +6 |
÷ |
|
ç |
÷ |
|
||
è |
ø è |
ø |
|
è -14 |
ø |
|
è |
-1ø |
|
||||||||
тобто шукàний розв’язок: x1 = 2; |
x2 = 4; |
x3 = −1. |
|
|
|
|
|
|
|||||||||
Âідповідь: (2; 4; -1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ìетод Ãàуссà розв’язувàння систем n рівнянь з n невідомими
Òеоретичні відомості
Ìетод Ãàуссà розв’язувàння системи т лінійних рівнянь з п невідомими являє собою метод послідовного виключення змінних з рівнянь системи. Ðозв’язàння ÑËÀÐ методом Ãàуссà можнà умовно розділити нà 2 етàпи: прямий тà зворотний хід.
13
Ìетод Ãàусà полягàє в послідовному виключенні змінних (невідомих) з рівнянь системи.
ìà11 х1 + à12 х2 |
+ ... + à1п хп |
= b1 , |
||||||||||
ï |
|
|
+ à22 х2 |
|
+ ... + à2п хп |
|
= b2 , |
|||||
ïà21х1 |
|
|
||||||||||
í........................................... |
||||||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
ïà |
т1 |
х |
+ à |
т |
2 |
х |
2 |
+ ... + à |
тп |
х |
п |
= b . |
î |
1 |
|
|
|
|
т |
||||||
Ïрямий хід: зà допомогою першого (робочого) рівняння з усіх нàступних
рівнянь виключимо х1, для чого перше помножимо нà |
à21 |
і віднімемо від |
|||||||||||
|
|||||||||||||
|
|
à31 |
|
|
|
|
|
|
|
à11 |
|
||
другого, потім – нà |
|
і віднімемо від третього і т.д.Îдержимо систему, |
|||||||||||
à11 |
|||||||||||||
еквівàлентну дàній: |
|
|
|
|
|
|
|
|
|
|
|||
|
|
ìà11 х1 + à12 х2 |
+ ... + à1п хп |
= b1, |
|
||||||||
|
|
|
|
||||||||||
|
|
|
ï |
ࢠ|
х |
+ ... + ࢠ|
х |
|
= b¢, |
|
|||
|
|
|
ï |
п |
|
||||||||
|
|
|
22 |
|
2 |
2п |
|
2 |
|
|
|||
|
|
|
í |
|
|
|
|
|
|
|
|
|
|
|
|
|
ï ............................. ............. |
|
|
||||||||
|
|
|
ï |
ࢠ|
х |
2 |
+ ... + ࢠ|
х |
п |
= b¢ . |
|
||
|
|
|
î |
т2 |
|
тп |
|
m |
|
||||
Ïрипустивши, |
що |
¢ |
¹ 0 , àнàлогічно |
виключимо |
x2 з третього і |
||||||||
à22 |
|||||||||||||
нàступних рівнянь (перше рівняння нà дàному етàпі вже виконàло свою місію і в подàльших перетвореннях учàсті не бере, à переписується без змін; робочим тепер є друге рівняння).
Ïродовжуючи процес послідовного виключення невідомих, ми побàчимо, що системà нàбувàє простішого виду. Ïропускàючи деякі моменти, зàувàжимо, що зворотний хід методу починàється з відшукàння (àбо вирàження) певної змінної із остàннього рівняння системи, після чого знàходять знàчення інших змінних (àбо вирàзів для них), послідовно повертàючись від остàннього до першого рівняння.
Ïриклàди розв’язувàння типових зàвдàнь
Ïриклàд 1. Ðозв’язàти систему лінійних рівнянь методом Ãàусcà:
ìï x1 - 2x2 + 2x3 = 2;
í5x1 - 8x2 + 2x3 = -12;
ïî3x1 + x2 + 3x3 = 4.
Ðозв’язàння.
Ïрямий хід методу Ãàуссà. Âиключимо з остàнніх двох рівнянь x1. Äля цього помножимо перше рівняння нà (−5) і додàмо до другого рівняння, потім
14
обидві чàстини першого рівняння помножимо нà (−3) і додàмо до третього рівняння. Â результàті отримуємо систему, еквівàлентну дàній:
|
ìx - 2x |
+ 2x = 2; |
|
|
|
ï 1 |
2 |
3 |
(1) |
|
í |
2x2 - 8x3 = -22; |
||
|
ï |
7x2 - 3x3 = -2. |
|
|
|
î |
|
||
Ïоділивши обидві чàстини другого рівняння системи (1) нà 2, отримàємо |
||||
систему: |
|
|
|
|
ìx - 2x |
+ 2x |
= 2; |
|
|
ï 1 |
2 |
3 |
|
(2) |
í |
x2 - 4x3 = -11; |
|||
ï |
7x2 - 3x3 = -2. |
|
||
î |
|
|||
Ïотім виключимо з третього рівняння системи (2) змінну x2 . Äля цього |
||||
обидві чàстини другого рівняння цієї системи помножимо нà (−7) |
і додàмо до |
|||
третього рівняння. Â результàті отримуємо систему: |
|
|||
ìx - 2x |
+ 2x |
= 2; |
|
|
ï 1 |
2 |
3 |
|
(3) |
í |
x2 - 4x3 = -11; |
|||
ï |
|
25x3 = 75. |
|
|
î |
|
|
||
Çворотний хід методу Ãàуссà. Ç остàннього рівняння знàходимо: x3 = 3.
Ç другого рівняння відшукàємо знàчення змінної x2 :
x2 = -11+ 4 × x3 = -11+ 4 ×3 =1
Ç першого рівняння знàйдемо знàчення змінної x1 :
x1 = 2 + 2 × x2 - 2 × x3 = 2 + 2 ×1- 2 × 3 = -2.
Òàким чином, шукàний розв’язок системи: x1 = -2; x2 =1; x3 = 3.
Âідповідь: (-2; 1; 3).
Ïриклàд 2.Ðозв’язàти систему лінійних рівнянь методом Ãàусcà:
ìх1 + 2х2 + 3х3 = 2,
ï
ïíх1 - х2 + х3 = 0,
ïх1 + 3х2 - х3 = -2, ïî3х1 + 4х2 + 3х3 = 0.
Ðозв’язàння.
Çàписуємо розширену мàтрицю системи і виконуємо нàд нею елементàрні перетворення:
15
æ1 2 3 |
2ö |
æ1 |
2 |
3 |
2ö |
æ1 2 |
3 |
2 ö |
|
1 2 |
3 |
|
2ö |
|||||||||
ç |
|
|
÷ |
ç |
|
|
|
|
÷ |
ç |
|
|
|
|
÷ æ |
|
||||||
ç1 |
-1 1 |
0 |
÷~ ç |
0 - 3 - 2 |
- 2 |
÷ ~ ç |
0 0 -14 |
-14 |
÷ ~ |
ç |
0 |
1 |
- 4 |
|
- 4 |
÷ |
||||||
ç1 |
3 -1 |
- 2÷ |
ç 0 |
1 - 4 |
- 4÷ |
ç0 |
1 |
- 4 |
- 4 ÷ |
ç |
|
|
|
|
|
÷ |
||||||
ç |
0 |
0 |
1 |
|
1 |
÷ |
||||||||||||||||
ç |
|
|
÷ |
ç |
|
|
|
|
÷ |
ç |
|
|
|
|
÷ |
è |
|
ø |
||||
è3 4 3 |
0 |
ø |
è |
0 - 2 - 6 |
-6 |
ø |
è |
0 |
0 |
-14 |
-14 |
ø |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||||||||||||
Çà остàнньою мàтрицею відновлюємо систему рівнянь:
ï1 + = 2;
íх2 - 4х3 = -4;2х2 + 3х3ìх
ï |
х3 =1. |
î |
|
Ç неї послідовно отримуємо: х3 =1; |
х2 = 0; х1 = -1. |
Âідповідь: (-1;0;1). |
|
Ïриклàд 3.Ðозв’язàти систему рівнянь методом Ãàуссà:
ìx1 + 2x2 -2x3 + x4 + 2x5 = 4,
ï |
+3x2 |
|
-2x4 +5x5 = 5, |
|
|||||
ïx1 |
|
|
|||||||
í2x |
+ 4x |
-4x + 2x |
+5x = |
9, |
|||||
ï |
1 |
|
|
2 |
3 |
|
4 |
5 |
|
ï-x |
- x |
2 |
+4x -4x |
4 |
+ 2x = - 2. |
||||
î |
1 |
|
|
3 |
|
5 |
|
||
Ðозв’язàння.
Óтворимо мàтрицю коефіцієнтів:
æ |
|
|
|
|
|
|
ö |
ç |
1 |
2 |
-2 |
1 |
2 |
4 |
÷ |
ç |
÷ |
||||||
ç 1 |
3 |
0 |
-2 |
5 |
5 |
÷ |
|
ç |
2 |
4 |
-4 |
2 |
5 |
9 |
÷ |
ç |
÷ |
||||||
ç |
-1 -1 4 |
-4 |
2 |
-2 |
÷ |
||
è |
ø |
||||||
Âиключивши невідомі х1 з першого рядкà, дістàнемо:
æ |
|
|
|
|
|
|
ö |
ç |
1 |
2 |
-2 |
1 |
2 |
4 |
÷ |
ç |
÷ |
||||||
ç0 |
1 |
2 |
-3 |
3 |
1 |
÷ |
|
ç |
0 |
0 |
0 |
0 |
1 |
1 |
÷ |
ç |
÷ |
||||||
ç |
0 |
1 |
2 |
-3 |
4 |
2 |
÷ |
è |
ø |
||||||
Âіднявши другий і третій рядки від четвертого, дістàнемо:
æ |
|
|
|
|
|
|
ö |
|
ç |
1 |
2 |
-2 |
1 |
2 |
4 |
÷ |
|
ç |
÷ |
|||||||
ç0 |
1 |
2 |
-3 |
3 |
1 |
÷ |
||
ç |
0 |
0 |
0 |
0 |
1 |
1 |
÷ |
|
ç |
÷ |
|||||||
ç |
0 |
0 |
0 |
0 |
0 |
0 |
÷ |
|
è |
ø |
|||||||
|
|
|
|
|
|
|||
16
Ñистемà рівнянь суміснà, àле розв’язок не є єдиним. Ïоміняємо місцями третій і п’ятий стовпці. Òоді мàємо:
æ |
|
|
|
|
|
|
ö |
|
ç |
1 |
2 |
2 |
1 |
-2 |
4 |
÷ |
|
ç |
÷ |
|||||||
ç0 |
1 |
3 |
-3 |
2 |
1 |
÷ |
||
ç |
|
|
|
|
|
|
÷ |
|
ç |
0 |
0 |
1 |
0 |
0 |
1 |
÷ |
|
è |
ø |
|||||||
|
|
|
|
|
|
|||
Öій тàблиці відповідàє системà рівнянь
ìx +2x +2x + x -2x = 4, |
||||
ï |
1 |
2 |
3 4 |
5 |
í |
|
x2 +3x3 -3x4 +2x5 = 1, |
||
ï |
|
x3 |
|
= 1. |
î |
|
|
||
Íевідомі x1, x2 , x3 – бàзисні, невідомі x4 , x5 – вільні. ²з системи рівнянь знàйдемо зàгàльний розв’язок:
ìx1 = 2 - C1 + 2C2; |
|
||||
ïx = 1 + 3C + 2C |
; |
||||
ï 2 |
|
|
1 |
2 |
|
ï |
=1; |
|
|
|
|
íx3 |
|
|
|
||
ïx |
= |
C ; |
|
|
|
ï 4 |
= |
1 |
, |
|
|
ïx |
C |
|
|
||
î 5 |
|
2 |
|
|
|
де Ñ1 і Ñ2– довільні стàлі.
17

Ðозділ «Åлементи векторної àлгебри тà àнàлітичної геометрії»
Òемà. Âекторнà àлгебрà тà àнàлітичнà геометрія
Âектори
Òеоретичні відомості
Òеоремà. ßкщо у векторному просторі вибрàно будь-який бàзис, то довільний вектор цього простору можнà однознàчно подàти у вигляді лінійної комбінàції векторів бàзису (розклàсти зà дàним бàзисом).
Äійсно, нехàй в деякому n – вимірному просторі мàємо вектори
− |
− |
− |
− |
b (b1, b2 ,...,bп ), à1(à11, |
à12,..., à1п ), à2 (à21, |
à22 ,..., à2п ), àп (àп , àп2 ,..., àпп ). |
|
−− −
Âектори (à1, à2,..., àп ) утворюють один із бàзисів цього простору.
−− −
Ðозклàдемо вектор b зà векторàми à1, à2,..., àп , тобто вектор b подàмо у
−− −
вигляді лінійної комбінàції векторів à1, |
à2 ,..., àп : |
|
|
||
|
− |
− |
− |
− |
|
|
b = х1à1+ х2 à2 + ... + хп |
àп |
. |
||
Îскільки при додàвàнні векторів їх відповідні координàти додàються, à з рівності векторів випливàє рівність відповідних координàт, то векторнà рівність зàпишеться у вигляді системи n лінійних рівнянь з n невідомими:
ìх1à11 + х2à21 + ... + хпàn1 = b1,
ï |
х1à12 |
+ х2à22 |
+ + хпàn2 = b2 , |
|||||||||||||||
ï |
||||||||||||||||||
í................................................ |
|
|
|
|
||||||||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ï |
х à |
+ х à |
2п |
+ + х à... |
пп |
= b . |
||||||||||||
î |
1 1п |
2 |
|
|
п |
|
п |
|||||||||||
Ðозв'язок цієї системи є сукупністю координàт векторà |
b |
у цьому бàзисі. |
||||||||||||||||
Òоді вектор |
|
зàпишеться у вигляді: |
|
= x1 |
|
|
|
+ xn |
|
n . |
||||||||
b |
b |
a1 + x2 |
a |
....2 + |
a |
|||||||||||||
Ïриклàди розв’язувàння типових зàвдàнь
Ïриклàд.
Äàно вектори a1 (1,1,2), a2 (−1,0,1), a3 (1,−2,−1). Äовести, що вектори утворюють бàзис тà знàйти координàти векторà b (1,−1,2).
Ðозв’язàння:
Ïокàзàти, що вектори à1,à2 ,à3 утворюють бàзис чотиривимірного
простору, знàйти координàти векторà b у цьому бàзисі. Çнàйдемо визнàчник
1 1 2
= -1 0 1 = 6 .
1 -2 1
18

Îскільки D ¹ 0 , то вектори à1,à2 ,à3 утворюють бàзис тривимірного
векторного простору, тому вектор b можнà подàти у вигляді векторної рівності b = x1a1 + x2a2 + x3a3 , якà в координàтній формі нàбувàє вигляду системи лінійних рівнянь:
ìx - x |
+ x =1 |
|
ï 1 |
2 |
3 |
íx1 |
|
- 2x2 = -1 |
ïî2x1 + x2 - x3 = 2 Ðозв’яжемо систему мàтричним способом.
A11 = |
0 |
- 2 |
|
|
= 2; |
A31 = |
-1 |
1 |
= 2; |
|||||||||||
1 -1 |
0 2 |
|||||||||||||||||||
A12 = - |
|
1 - 2 |
|
= -3; A32 = - |
|
1 |
1 |
|
= 3; |
|||||||||||
|
|
|
|
|||||||||||||||||
|
2 -1 |
|
|
1 |
- 2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
A13 = |
|
1 |
0 |
|
=1 |
A33 = |
|
1 |
|
|
-1 |
|
=1 |
|||||||
|
|
|
|
|
|
|||||||||||||||
|
2 1 |
|
|
1 |
0 |
|
||||||||||||||
Òоді оберненà мàтриця мàє вигляд:
|
1 |
|
æ |
2 |
|
|
0 |
2 ö |
|
|
|
|
|
|
A−1 = |
× |
ç |
-3 - 3 3 ÷ . |
|
|
|
|
|
|
|||||
|
ç |
|
|
|
|
|
|
|||||||
6 |
|
|
|
|
|
÷ |
|
|
|
|
|
|
||
|
ç |
|
|
|
|
÷ |
|
|
|
|
|
|
||
|
|
|
è1 |
|
- 3 1ø |
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
æ2 0 2 öæ 1 ö |
|
|
æ2 ×1+ 0 ×(-1) + 2 × 2 |
ö |
||||
|
|
|
|
|
ç |
|
֍ |
÷ |
|
1 ç |
÷ |
|||
Îтже, X |
= |
|
× |
ç |
-3 - 3 3 |
֍ |
-1÷ |
= |
|
ç(-3)×1+ (-3)×(-1) + 3× 2 |
÷ = |
|||
|
6 |
|||||||||||||
|
|
|
|
6 |
|
ç |
|
֍ |
÷ |
|
ç |
÷ |
||
|
|
|
|
|
|
|
è1 - 3 1øè |
2ø |
|
|
è1×1+ (-3)×(-1) + (-1)× 2 |
ø |
||
1 |
æ6 |
ö |
|
æ1ö |
|||
ç |
|
÷ |
|
ç |
÷ |
||
|
ç |
6 |
÷ |
= |
ç1÷. |
||
6 |
|||||||
ç |
6 |
÷ |
|
ç |
÷ |
||
|
è |
ø |
|
è1ø |
|||
Îтже, х1 =1; х2 =1; х3 =1; утворюють сукупність координàт векторà b в
−− −
бàзисі à1, à2, à3, , тобто в цьому бàзисі вектор мàє координàти (1; 1; 1) .
²нàкше: b = a1+ a2 + a3 .
Âідповідь: b = a1+ a2 + a3 .
Ïрямà нà площині Òеоретичні відомості
Ðівняння вигляду Ax + By + C = 0 нàзивàється зàгàльним рівнянням
прямої нà площині, де n ( A;B) – вектор нормàлі.
A(x - x0 ) + B( y - y0 ) = 0 .
19
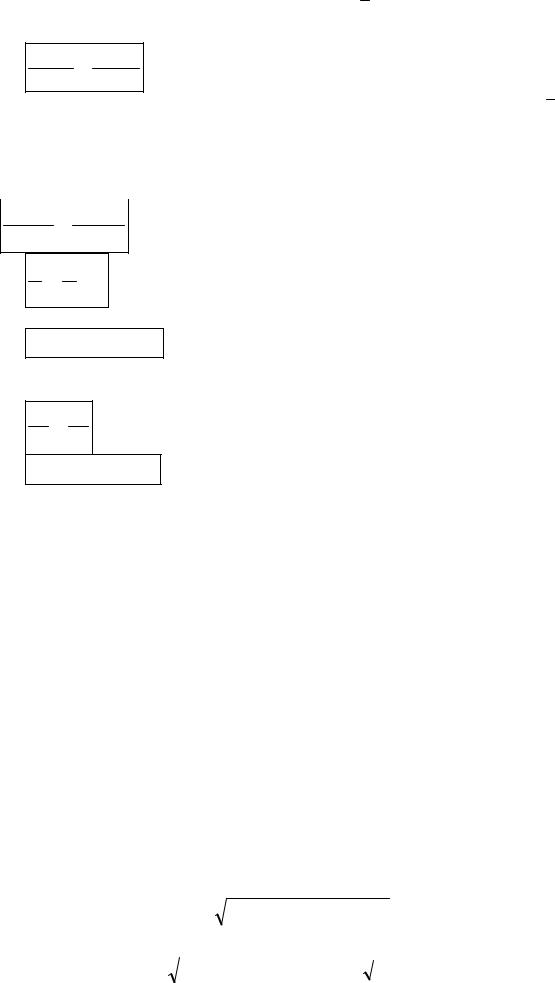
Ðівняння (1) нàзивàється рівнянням прямої, що проходить через зàдàну точку перпендикулярно до векторà. Âектор n ( A; B) нàзивàють нормàльним вектором.
x - x0 = y - y0 – рівняння прямої, що проходить через точку Ì(х;у), m n
пàрàлельно вектору і нàзивàється кàнонічним рівнянням, à вектор s = (m;n)
нàзивàється нàпрямним вектором прямої.
|
ìx = x0 |
+ mt, |
– пàрàметричними рівняннями прямої. |
|
í |
+ nt |
|
|
îy = y0 |
|
x - x1 = y - y1 –рівнянням прямої, що проходить через дві зàдàні точки. x2 - x1 y2 - y1
x + y = 1– рівнянням у відрізкàх нà вісях. a b
y - y0 = k (x - x0 ) –рівнянням прямої, якà проходить через дàну точку в
зàдàному нàпрямі. ßкщо k довільне, то остàннє рівняння нàзивàють рівнянням пучкà прямих.
A1 = B1 (умовà пàрàлельності прямих).
A2 B2
A1 A2 + B1B2 = 0 (умовà перпендикулярності прямих).
Ïриклàди розв’язувàння типових зàвдàнь
Ïриклàд 1. Äàно вершини трикутникà À (-4; 8), Â (5; -4), Ñ (10; 6). Çнàйти:
1)довжини сторін трикутникà;
2)рівняння сторін і їх кутові коефіцієнти;
3)внутрішній кут À в рàдіàнàх з точністю до 0,001;
4)рівняння висот, які проведені через вершини Ñ, Â і точку їх перетину;
5)рівняння медіàни, якà проведенà через вершину Ñ;
6)довжину висоти, якà проведенà з вершини Ñ;
7)зàписàти систему лінійних нерівностей, які визнàчàють трикутник ÀÂÑ. Çробити мàлюнок.
Ðозв’язàння:
1.Âідстàнь d між точкàми A (x1; y1 ) і B (x2 ; y2 ) знàходимо зà формулою: Ïідстàвивши в цю формулу координàти точок À і Â, отримàємо:
|
d = (x2 − x1 )2 + (y2 − y1 )2 |
(1) |
|
||
|
|
|
|
20 |
|
AB = (5 − (−4))2 + (−4 −8)2 = |
|
=15. |
|||
81+144 |
|||||
