04. Основные постулаты квантовой механики

Основные постулаты квантовой механики

http://www.novgorod.ru/rus/other/fizika/4.htm

В основе квантовой механики лежит несколько постулатов. Мы их просто введем, а их смысл станет ясным из дальнейшего изложения.

Первый постулат утверждает, что каждую физическую величину можно представить линейным оператором.

Второй состоит в том, что в результате измерения физической величины F, представленной оператором , может получиться лишь одно из собственных значений Fm оператора .

Третий постулат квантовой механики утверждает, что при измерениях, осуществляемых над системой, находящейся в состоянии, определяемом волновой функцией , вероятность получить значение Fm физической величины F равна квадрату модуля коэффициента cm разложения

волновой функции по собственным функциям оператора .

1. Квантовомеханические операторы

Для квантовой механики необходим соответствующий математический аппарат, который должен соответствовать физической постановке квантовомеханических задач. Такой аппарат был разработан в математике. Это теория линейных операторов.

Под оператором будем понимать правило, по которому одна функция (x1, x2, ...) переменных x1, x2, ... сопоставляется с другой функцией (x1, x2, ...) тех же переменных. В дальнейшем операторы мы будем обозначать при помощи букв со шляпкой. Т.е. правило перехода от функции к функции запишем в виде

.

Оператор может означать дифференцирование по какой-то переменной

.

Символически этот оператор записывается в виде

.

Оператор независимой переменной опеределим как умножение на эту переменную = x

.

В операторном виде может быть представлено также и интегральное соотношение между функциями и

.

Функция носит название ядра интегрального оператора .

Определим линейный оператор как такой оператор, для которого выполнены равенства

,

где C - произвольная постоянная. Отсюда следует, что

,

где C1 и C2 - произвольные постоянные.

Комбинируя два заданных оператора и 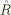, можно определить их сумму и произведение. Под суммой операторов понимается оператор , определенный соотношением

= + ,

= + .

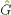Под произведением двух операторов и понимается оператор = , заключающийся в последовательном применении операторов и

.

Если же сначала применяется оператор , а затем оператор , то их произведением будет оператор

.

Заметим, что операторы и ', вообще говоря, не совпадают между собой, т.е. произведение операторов существенно зависит от порядка сомножителей. В соответствии с этим алгебра операторов - это алгебра некоммутирующих величин. Два оператора называются коммутирующими между собой, если произведение операторов не зависит от порядка сомножителей, и некоммутирующими в противоположном случае. В качестве примера найдем произведение оператора дифференцирования по x на оператор умножения на x при обоих порядках сомножителей.

.

Оператор = 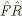равен

.

Найдем оператор ' =

.

Таким образом,

,

и не совпадает с оператором '. Поэтому операторы и ' не коммутируют. Разность этих двух

операторов

(IV.1)

называется коммутатором и обозначается

Понятие коммутатора носит в квантовой механике фундаментальную роль. Физические величины, операторы которых коммутируют между собой, могут быть измерены одновременно. Физические величины, операторы которых не коммутируют, не могут быть одновременно измерены. Так, одновременно невозможно измерить положение частицы и ее импульс, поскольку их коммутатор отличен от нуля (см. ниже).

Стоящую в операторном соотношении (IV.1) единицу называют единичным оператором.

Если в качестве оператора 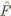взять оператор умножения на другую независимую переменную y, то операторы и ' коммутируют:

.

2. Собственные значения и собственные функции операторов

Рассмотрим операторное соотношение

(IV.2),

где - любой линейный оператор: матрица, дифференциальный оператор, интегральный оператор и т.д. При том - определенный объект в зависимости от вида . Если -

дифференциальный оператор, то - функция, если - матрица, то - вектор-столбец. Решения уравнения (IV.2) называются соответственно собственными функциями, собственными векторами

ит.п. Избранные значения параметра , для которых существуют нетривиальные решения уравнения (IV.2), называют собственными значениями.

Впростейшей квантовомеханической задаче о движении частицы в потенциальной яме с бесконечными стенками решается уравнение (IV.2) с дифференциальным оператором d2/dx2. Граничные условия приводят к собственным значениям

исобственным функциям

.

Совокупность собственных значений оператора называется его спектром. Очевидно, что в случае потенциальной ямы с бесконечными стенками, спектр оператора дискретный.

Если же мы не требуем обращения функции в нуль на границах промежутка (0,l) для того же вида оператора, то собственные функции будут иметь вид

для всех значений k2 > 0. В этом случае спектр (совокупность собственных значений) называется непрерывным.

В случае дискретного спектра собственных значений соответствующие собственные функции квадратично интегрируемы. Собственные функции, соответствующие сплошному спектру, - квадратично неинтегрируемы.

Если каждому собственному значению оператора принадлежит одна и только одна собственная функция , спектр называется невырожденным. Если же собственному значению оператора принадлежит несколько собственных функций (например r), то данное собственное значение называется вырожденным с кратностью r.

3. Эрмитовы операторы

Вклассической механике состояние системы определяется совокупностью координат и импульсов, определяемых уравнениями движения. Все величины, характеризующие состояние системы, называют механическими величинами.

Вквантовой механике величины, играющие аналогичную роль, называются квантовомеханическими величинами, или физическими, или динамическими переменными.

Основное положение квантовой механики состоит в следующем: каждой квантовомеханической величине F соответствует некоторый эрмитовый оператор ; спектр

собственных значений оператора представляет спектр возможных (измеряемых) значений этой величины. Требование эрмитовости оператора связано с вещественностью значений реальных физических величин.

Оператор называется эрмитовым (самосопряженным) оператором, если

(IV.3),

где под * * понимается

.

Покажем, что собственные значения эрмитовых операторов вещественны. Для простоты рассмотрим случай, когда оператор обладает дискретным спектром.

.

Умножим уравнение слева на n* и, проинтегрировав, получим

.

С другой стороны, используя (IV.3)

.

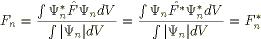Поэтому собственные значения эрмитового оператора вещественны, как и должно быть для реальных физических величин.

В качестве примера найдем оператор, сопряженный к оператору дифференцирования

. Полагая, что функции 1 и 2 обращаются в нуль, на бесконечности получим, производя интегрирование по частям,

(IV.4)

Поэтому сопряженный оператор +

не совпадает с оператором , т.е. условие (IV.3) не выполняется - оператор дифференцирования не является самосопряженным (или эрмитовым). Однако, если умножить оператор дифференцирования на величину -iћ, то очевидно, что такой оператор будет эрмитовым (самосопряженным). Обозначим этот оператор через Px.

.

Этот оператор называется оператором импульса.

В трехмерном случае имеем три компоненты

,

а оператор импульса выражается как

.

Является ли эрмитовым оператор d2/dx2?

.

Здесь мы опять применили метод интегрирования по частям и использовали тот факт, что функции 1 и 2 исчезают на бесконечности. Еще раз интегрируя по частям, получим

.

Таким образом, оператор d2/dx2 является самосопряженным оператором, и самосопряженным оператором будет оператор

,

который представляет собой оператор кинетической энергии

.

В трехмерном случае

.

Очевидно, что оператор координаты, представляющий собой оператор умножения на величину координаты

= x ,

является эрмитовым, так как

.

Таким образом, операторы таких динамических (физических) переменных, как координата, импульс, кинетическая энергия, являются эрмитовыми (самосопряженными) операторами, и их собственные значения будут вещественными.

Кроме этих операторов введем оператор углового момента

,

как векторное произведение оператора координаты и оператора импульса. В компонентах

Компоненты момента не коммутируют между собой. Коммутируют только лишь квадрат момента с любой из компонент, например,

Это означает, что одновременно могут быть измерены лишь величина момента и одна из его проекций, в нашем случае проекция на ось z.

4. Ортогональность и нормировка собственных функций эрмитовых операторов

Собственные функции линейного эрмитового оператора , отвечающие различным собственным значениям Fn и Fm, взаимно ортогональны, т.е. удовлетворяют соотношению

.

Действительно, функции n и m* удовлетворяют уравнениям

,

.

Поскольку оператор эрмитов, соотношение

эквивалентно

,

или

.

Поскольку Fm Fn, то для того, чтобы последнее равенство выполнялось, необходимо

.

Так как собственные функции удовлетворяют линейному однородному уравнению, то они определены с точностью до произвольной постоянной. Мы будем нормировать собственные функции дискретного спектра условием

.

Условие ортогональности и нормировки в этом случае запишется в виде

,

где символ Кроникера

.

В случае непрерывного спектра условие ортогональности и нормировки запишется в виде

,

где - дельта-функция Дирака.

5. Волновая функция и вероятность результатов измерений физических величин

Предположим, что состояние системы описывается волновой функцией . Пусть представляет некоторый квантовомеханический оператор, для которого можно написать

Для простоты будем считать, что оператор имеет дискретный спектр собственных значений Fn, и каждому из них отвечает одна собственная функция (спектр невырожденный).

Система собственных функций произвольного линейного самосопряженного оператора является полной системой ортогональных функций. Поэтому произвольную непрерывную функцию, определенную в той же области изменения независимых переменных и

удовлетворяющую широкому классу условий, можно разложить по этой системе собственных функций. Предполагая n нормированными на единицу, разложим функцию (x) в ряд

Амплитуду cn можно определить, воспользовавшись ортогональностью собственных функций. Умножая последнее уравнение на m* и интегрируя по всей области изменения независимых переменных, получаем

В силу ортогональности собственных функций из всех членов суммы, стоящей в правой части, отличен от нуля только член с n = m. Соответственно имеем

На основании принципа суперпозиции мы можем заключить, что состояние системы, описываемое волновой функцией (x), может быть представлено в виде суперпозиции состояний

с определенными значениями Fn физической величины .

Амплитуда cm показывает, с каким весом в состоянии (x) представлено состояние m(x).

Иными словами, амплитуда cm характеризует вероятность того, что при измерениях величины , производимых над системой, находящейся в состоянии, определяемом волновой функцией (x), будет обнаружено значение, равное Fm. В квантовой механике принимается, что указанная вероятность равна квадрату модуля амплитуды разложения |cm|2. Таким образом, если мы хотим найти вероятность того, что при измерениях, производимых над системой в состоянии , для физической величины F будет найдено значение Fm, следует разложить волновую функцию (x)

по собственным функциям оператора . Квадрат модуля соответствующей амплитуды разложения |cm|2 дает искомую вероятность, причем

6. Средние значения физических величин

Предположим, что состояние системы описывается волновой функцией (x), которая не

является собственной функцией оператора , отвечающего квантовомеханической величине F. Это означает, что в данном состоянии величина F не имеет определенного значения. При измерениях, производимых над системой, может получиться любое собственное значение Fn. В этом случае в квантовой механике физическая величина определяется ее средним значением

,

где Wn - вероятность получить при измерении физической величины F собственное значение Fn. Используя выражение для вероятности

имеем для случая дискретного спектра

или

Окончательно имеем

Если волновая функция является собственной функцией оператора , то величина F имеет вполне определенное значение, равное собственному значению Fm. При этом, как и следовало ожидать, среднее значение величины F совпадает с этим собственным значением

7. Соотношение неопределенности Гейзенберга

В квантовой механике имеется следующее положение: невозможно измерить одновременно импульс частицы и ее местоположение со сколь угодно большой точностью. Допустимые точности удовлетворяют условию

(IV.6).

Это условие носит название принципа неопределенности Гейзенберга.

Рассмотрим свободную частицу, импульс которой не имеет строго определенного значения, но может лежать в малом интервале p около значения p0 (мы для простоты рассматриваем случай одномерного движения). Согласно принципу суперпозиции, волновую функцию электрона можно записать в виде

.

Оценивая интервал для малых k, имеем

.

Это выражение показывает, что суперпозиция волновых функций, отвечающих близким значениям импульсов, приводит к образованию волнового пакета, перемещающегося с групповой скоростью

.

Из вида волновой функции ясно, что вероятность обнаружить микрочастицу в точке x в момент времени t имеет резкий максимум, который движется со скоростью vгр. Этот волновой пакет обладает пространственной протяженностью, величина которой удовлетворяет условию

(IV.7) .

Поэтому с подавляюще большой вероятностью измерения координаты электрона покажут, что он будет обнаружен в области пространства x. В этом смысле можно говорить, что координата электрона определена с точностью до величины x. При этом, однако, электрон, находящийся в области x, не описывается плоской волной и не имеет определенного значения импульса. Для образования волнового пакета шириной x необходимо создать суперпозицию плоских волн в

интервале с p, удовлетворяющему условию (IV.7) (более точно (IV.6)). Это означает, что измерения импульса электрона, локализованного в области x, будут приводить к значениям импульса, лежащим в указанном интервале. Иными словами, неопределенность в значении координаты электрона x (локализованного в области x) и неопределенность в значении его импульса p связаны соотношением (IV.6). Чем меньше ширина пакета x, тем больше р. Напротив, если задан интервал импульсов р, то формула (IV.6) показывает, что частица с подавляюще большой вероятностью будет обнаружена в области

пространства размером .

Из условия (IV.6) следует, что величины х и p не могут быть равны нулю одновременно. Это означает, что координата x и сопряженный с ней импульс p не могут одновременно иметь вполне определенное значение. Таким образом, классические понятия пространственного

положения и величины импульса применимы к частице в определенных пределах, даваемых соотношением Гейзенберга. Всякая попытка одновременно применить к частице понятия импульса и координаты с большей точностью, вне рамок соотношения неопределенности, не имеет смысла. Это обстоятельство связано с самой природой частиц, с их корпускулярноволновыми свойствами.

Рассмотрим для примера треки электрона в камере Вильсона, которые представляют собой капельки жидкости на образованных электроном ионах. Размеры капелек дают степень точности, с которой может быть фиксирована координата частицы. Поскольку размеры капелек порядка 10- 4 см, неопределенность в координате электрона также имеет порядок 10-4 см. Следовательно,

неопределенность соответствующей компоненты импульса 10-23 г·см/сек. Т.к. масса электрона равна 10-27 г, то неопределенность в составляющей скорости, направленной перпендикулярно треку, будет равна

см/сек.

Но следы в камере Вильсона оставляют лишь достаточно быстрые электроны, имеющие скорость

109 см/сек. Следовательно, в указанных условиях и приближенно можно говорить о движении частицы вдоль некоторой траектории в камере Вильсона.

Соотношение неопределенности Гейзенберга, записанное в виде

,

показывает, что понятия классической физики оказываются применимыми с тем большей степенью точности, чем больше масса частицы. Ввиду малости квантовой постоянной ћ, неопределенность в значениях координаты и скорости становится пренебрежительно малой у частиц макроскопически малого, но еще не атомного размера.

Пусть мы имеем тело размером 1 микрон с массой ~ 10-10г. Тогда

10-17 см2/cек.

Если, например, положение тела определено с точностью 10-6 см (1/100 его размера), то

10-11 см/cек.

Скорость броуновского движения частицы с массой 10-10 составляет ~ 10-4 см/cек. Мы видим, что погрешность в скорости, связанная с соотношением неопределенности, пренебрежимо мала уже у такого небольшого тела. Тем более она не играет роли у макроскопических тел.