Уханов - лекции

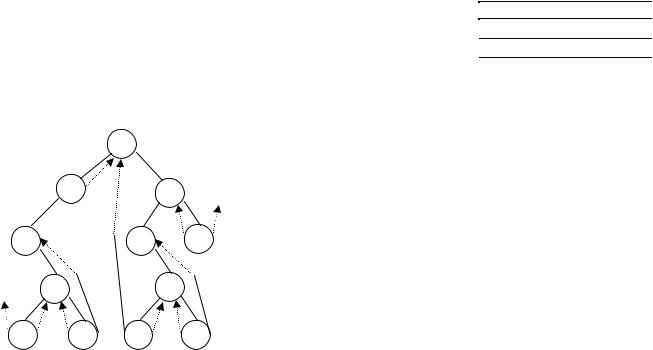
связей поместим указатели на некоторые другие узлы дерева. Эти связи будем называть “нитями” в отличие от основных. Чтобы отличать основные связи от нитей, заведем в каждом узле два однобитовых поля l и r, принимающих значения 1, если связь является нитью и 0, если связь является основной.

Обозначим *P и P* – соответственно указатели на предшественника и последователя узла P при обходе в обратном порядке.

Сопоставим обычное дерево и дерево, прошитое для обхода в обратном порядке:

Здесь вместо пустой связи будем хранить указатель на предшественника или последователя узла при обходе в обратном порядке.

a

Тогда прим обратном обходе получим последовательность: q e l d b a r s t f c g. Пунктирными линиями изображены связи-нити.

Если дерево прошито, то легко можно определить последователя для данного узла. Структура прошитого дерева:

typedef struct A {

... info; char r, l;

struct A *llink; struct A *rlink;

} UZEL;

Большое преимущество прошитых деревьев состоит в том, что упрощаются алгоритмы их прохождения. Сначала напишем функцию, возвращающую указатель на последователя в обратном порядке обхода.

UZEL* Next (UZEL *p) { if (p Æ r) {

p = p Æ rlink;

while (p Æ l) p = p Æ llink; return p;

} else {

return p Æ rlink;

}

}

Тогда обход дерева будет выглядеть очень просто.

найти узел P while (P != NULL) {

обработка (P); P = next (P);

}

Отметим, что алгоритм больше не является рекурсивным, поэтому необходимость в стеке для обхода прошитого дерева отпадает.

Для того, чтобы программы правильно работали с пустыми деревьями можно использовать голову, для которой исходное поддерево является левым поддеревом. В этом случае связи llink узла p и rlink узла g должны указывать на голову.

До сих пор представление деревьев производилось с помощью всюду прошитых или не прошитых деревьев. Существует промежуточный способ. Если отсутствует правая или левая прошивки дерева, то деревья называются соответственно право- и лево-прошитыми.

Так же можно определить прошивки для прямого и концевого обхода.

Деревья без связей

Подходящий выбор представления дерева в первую очередь определяется видом операций, выполняемых над деревьями. В частности, можно использовать методы последовательного распределения памяти. Этот способ является наиболее подходящим в случае, когда требуется компактное представление дерева, размеры и конфигурация которого в процессе выполнения программы не должны сильно изменяться. Два наиболее простых способа представления деревьев заключается в том, что опускается поле llink или rlink. Последовательное расположение узлов в памяти замечает связь одного из этих типов.

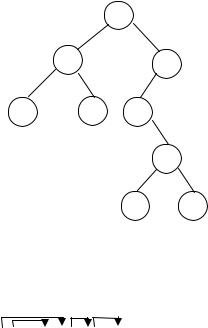
Пусть в дереве вообще не будут храниться левые связи. Левые связи отображаются с помощью физического соседства. Если узел имеет левого сына, то он лежит сразу за отцом. Рассмотрим на примере прямого обхода.

a

b f

q

s r

Прямой обход дает последовательность: a b c d f p q s r.

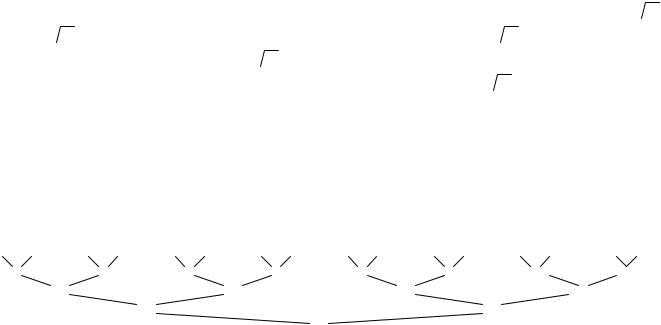
Обозначим символом отсутствие левого сына у узла, а стрелкой изобразим правую связь. Тогда дерево, не использующее поле llink можно изобразить:

a b c d f p q s r

Связь llink не нужна, так как она либо равна нулю, либо указывает на следующий элемент последовательности.

Предложенное представление дерева связано с непроизводительной тратой места, так как многие поля rlink пусты. Поэтому существует еще один способ представления дерева, основанный на последовательном использовании памяти – вообще без связей. Все узлы располагаются в

последовательной памяти (нумерация узлов ведется с единицы). Узел с номером X имеет узлы с номерами 2X и 2X+1 в качестве сыновей.

Т.е. для описанного выше дерева будем иметь следующую таблицу распределения памяти.

Преобразование дерева общего вида к бинарному

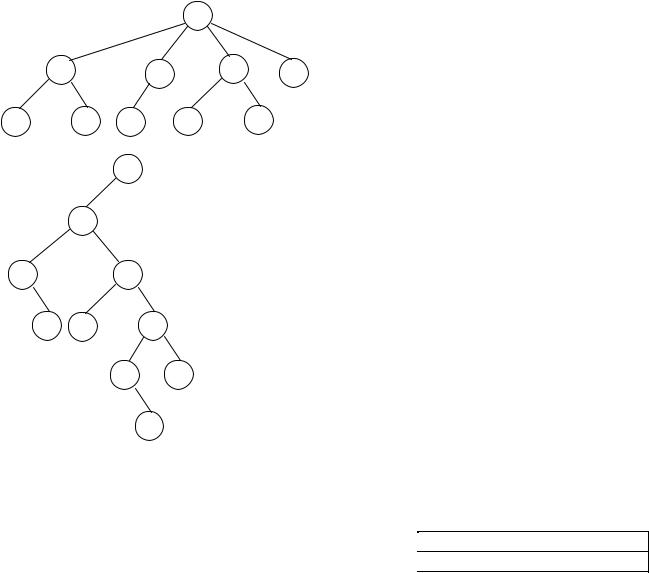
Всякое дерево можно представить в виде бинарного. Алгоритм преобразования следующий. Оставляем связь отца с самым левым сыном. Братьев свяжем правыми связями. Такой алгоритм гарантирует единственность преобразования.

Пример:

b

q e

t

Таблицы

Рассмотрим простейшую таблицу.

Одна строчка в таблице называется записью. Каждая колонка таблицы называется полем. Отличительную характеристику записи таблицы называют ключом или признаком. Все

операции над таблицами задаются по отношению к ключу, а выполняются над всей записью. Ключ – это аргумент поиска записей в таблице. Ключ может состоять из одного или

нескольких полей таблицы.

Ключ называется первичным, если поле или группа полей, составляющих ключ, уникальным образом определяют запись. Иначе поиск по первичному ключу можно определить как “найти единственную”. Первичный ключ не обязательно единственен.

Вторичный ключ не определяет запись уникальным образом, т.е. поиск “найти многие”. К типичным операциям над таблицами относят:

1.Включение: дана пара ключ-данные, требуется включить запись в таблицу так, чтобы впоследствии ее можно было найти по ключу.

2.Изменение: найти ключ, изменить данные записи.

3.Исключение: по заданному ключу исключить всю запись из таблицы.

4.Поиск: дан ключ, найти соответствующие данные.

Таблица может иметь индекс. Индексом называется таблица, состоящая из двух полей: ключа и номера записи.

Пример:

На одну таблицу можно навесить несколько индексов и сделать ее доступной. Существуют четыре способа организации таблиц:

•куча (последовательные);

•сортированные;

•древовидные;

•рассеянные.

В каждом конкретном случае следует выбирать наиболее подходящий способ, обеспечивающий эффективное выполнение требуемых операций.

Куча

Вставка.

Запись помещается либо в свободную позицию, либо в конец. Поиск.

Поиск производится последовательным перебором. Успешный поиск по первичному ключу потребует просмотра в среднем полтаблицы. Неудачный поиск (поиск того, чего в таблице нет) – просмотр всей таблицы. Поиск по вторичному ключу всегда требует просмотра всей таблицы.

Удаление.

Тут существует два способа.

1.Наивный. Запись физически удаляется. Все нижележащие записи перемещаются на позицию вверх. Эта операция требует просмотра половины всех записей таблицы.

2.Запись помечается как удаленная (* в первом байте записи рассматривается как пометка на удаление). Возникает проблема использования свободного пространства. Таким образом, помеченные на удаление записи придется рано или поздно удалять физически. Для этого используется операция упаковка (Pack). Лучше, чтобы этих операций было меньше.

Все операции над кучей требуют время, пропорциональное размеру таблицы. Следовательно, кучу целесообразно применять для небольших таблиц или когда скорость работы с таблицей не важна.

Сортированные таблицы

Вставка.

Существует два способа.

1.Наивный. Находим место вставки (например, методом дихотомии). Физически перемещаем вниз все записи от места вставки вниз. Затраченное время ~ N.

2.С каждой записью может быть ассоциирована область переполнения, которая может быть организована как куча, список, дерево. Дихотомией находится место вставки и если там не тот ключ, то обходим область переполнения, связанную с этой записью.

Поиск.

Поиск осуществляется методом дихотомии – деление отрезка пополам. Для поиска в массиве целых чисел можно предложить функцию:

//в массиве t размера n найти запись, соответствующую ключу key и вернуть ее номер. int dihot (int *t, int n, int key) {

int i, j, k; i = 0;

j = n - 1; while (i < j) {

k = (i + j) / 2;

if (t [k] < key) i = k; else j = k;

}

if (t [i] = = key) return i; else return -1;

}

Оценим время выполнения наиболее экономного алгоритма поиска. При каждом сравнении ключей ставится вопрос типа “совпадают ли ключи” или “больше-меньше”. Сравнение дает ответ “да-нет”. Таким образом, M сравнений дает 2M возможных исходов. Искомый ключ в таблице из N записей, может находиться в любом из N мест. Следовательно, требуется распознать N ситуаций,

т.е. количество исходов не должно быть меньше N: 2M ≥ N . Логарифмируя, получаем количество сравнений M ≥ log2 N .

Удаление.

Тоже два способа.

1.Наивный. Удалить физически и передвинуть следующие записи. Время выполнения ~ N.

2.Пометить запись как удаленную. Присоединить ее к списку свободного пространства нельзя, т.к. нарушится метод дихотомии. Потребуется обслуживание такой таблицы.

Оценка трудоемкости сортировки

Оценим трудоемкость процесса упорядочения массива из N ключей.

Для поиска первого элемента массива требуется M ≥ log2 N сравнений. Второй элемент будем искать уже среди N-1 элемента. Следовательно, требуется M ≥ log2 (N -1) сравнений. Чтобы найти последний элемент нужно M ≥ log21 сравнений. Таким образом, на сортировку массива потребуется следующее количество сравнений:

M ≥ log2 N +log2 (N −1) +... +log21 = log2 N (N −1) ... 1 = log2 N!.

Для вычисления N! воспользуемся формулой Стирлинга: N!= 2р N ( Ne )N .

С учетом этого, получим:

элемента использовалось время выполнения самого экономного алгоритма поиска, то данная оценка является оптимальной. На нее будем ориентироваться при рассмотрении различных методов сортировки.

Методы внутренней сортировки

Сортировка называется внутренней, если она происходит в оперативной памяти.

Простой выбор

Найти наименьшее из всех, поставить первым. От второго до конца найти наименьшее, поставить вторым и т.д.

Пример:

Сортировка целых чисел.

void SimpleChoice (int *t, int n) { int i, j, k;

for (i = 0; i < n-1; i ++) { k = i;

for (j = i+1; j < n; j ++) { if (t [j] < t [k]) k = j;

Таким образом, можно сделать вывод, что простой выбор является плохим методом, поскольку работает очень медленно (квадратичное время). Поэтому его можно применять только для небольших таблиц.

Сортировка подсчетом

Этот простой метод заключается в том, что j-й ключ упорядоченной последовательности превышает ровно j-1 ключей. Алгоритм сортирует записи по ключам, используя для подсчета числа ключей, предшествующих данному, массив счетчиков. После завершения работы j-й элемент массива счетчиков определяет окончательное положение j-й записи в таблице.

Пример:

Сортировка целых чисел.

void CalcSort (int *t, int n, int *c){ int i, j;

for (i = 0; i < n; i ++) c [i] = 0; //обнуляем массив счетчиков for (i = 0; i < n-1; i ++){

for (j = i+1; j < n; j ++){ if (t [i] < t [j]) c [j] ++; else c [i] ++;

}

}

}

Число сравнений ключей, очевидно равно N(N2 -1) , т.е. растет пропорционально N2 .

Простые вставки

Пусть первые k чисел уже отсортированы. Тогда среди этих чисел найдем место для вставки k + 1 ключа таким образом, чтобы он не нарушал порядок сортировки. Затем перейдем к

}

Оценим трудоемкость алгоритма. Ключ, находящийся в j-й позиции будет перемещаться в

Метод пузырька

Идем слева направо и сравниваем соседей. Если они стоят не по порядку, меняем их местами. Завершив один проход, начинаем новый и так до тех пор, пока в течение прохода не будет ни одного обмена местами. При выполнении этой последовательности операций запись с наибольшим ключом займет положение N, т.е. всплывет пузырек.

Пример:

Сортировка целых чисел. void Bubble (int *t, int n) {

b = 0;

for (i = 0; i < k; i ++) { if (t [i] > t [i+1]){

m = i;

b = 1;

t [i] ↔ t [i+1];

}

k = m;

}

}

Время работы алгоритма пропорционально N2.

Быстродействие можно улучшить, если просматривать массив ключей сначала слева направо (всплывают большие ключи), затем справа налево (всплывают маленькие ключи). Такой метод называется шейкер-сортировка. Время работы все равно пропорционально N2.

Квадратичный выбор

Быстродействие сортировки посредством простого выбора можно улучшить, если сделать процесс выбора более чем одноступенчатым. Пусть размер таблицы N=16. Разобьем таблицу на 4 группы по четыре элемента в каждой:

Определим наибольший элемент в каждой группе и помести м его в отдельную группу лидеров:

Наибольший среди них и есть наибольший в таблице. Поместим его в область вывода. Второй элемент и последующие отыскиваются следующим образом: среди элементов группы, из которой происходил выбранный на предыдущем шаге элемент, выбираем наибольший и помещаем вместо выбывшего в группу лидеров. Затем очередной элемент выбирается из группы лидеров.

Если количество записей N в таблице полный квадрат, то можно разделить таблицу на N групп по N элементов. Любой выбор, кроме первого, требует не более N -1 сравнений внутри группы ранее выбранного элемента и N -1 сравнений внутри группы лидеров. Таким образом,

время работы сортировки квадратичным выбором пропорционально N N , что гораздо лучше, чем N2, что получалось при сортировке простым выбором.

Эту идею можно обобщить, получив метод кубического выбора, выбора четвертой степени и т.д. Если развить эту идею до полного завершения, когда в группе на каждом уровне содержится только 2 элемента, то придем к методу, основанному на структуре бинарного дерева.

Выбор из дерева

В корень дерева попадает наибольший ключ. Чтобы выявить второй по величине ключ, нужно введенный элемент заменить на −∞, тогда в корень попадет второй ключ. Для этого следует изменить только один путь в дереве, для чего потребуется не более log2 N +1 сравнений.

Таким образом, время сортировки пропорционально N log2 N .

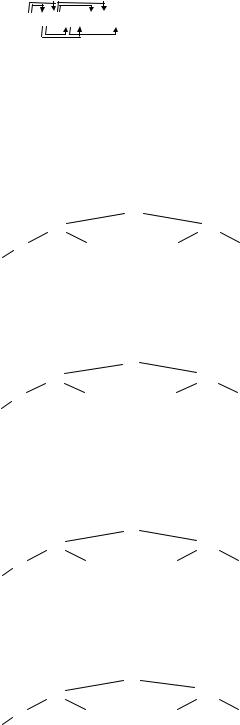
Чтобы знать, куда вставлять следующий элемент −∞, нужно помнить, откуда пришел ключ, находящийся в корне, поэтому узлы разветвления в действительности содержат указатели на позицию ключа, а не сам ключ. Отсюда следует, что необходима память для N исходных записей, N-1 указателей и N выводимых записей. Сортировку удобно проводить «восходящим методом»: выводится элемент из корня, перемещается вверх наибольший из его потомков, затем наибольший из потомков последнего и т.д. Восходящий метод позволяет избежать лишних сравнений с −∞.

Пирамидальная сортировка

Таблица располагается в последовательной памяти, на которую наложена структура бинарного дерева. Для j-й записи потомками являются записи с номерами 2j и 2j+1. Например, для некоторой последовательности ключей подразумеваемые связи бинарного дерева имеют вид

7 5 2 1 8 4 6 3

Будем называть таблицу пирамидальной, если все предки больше своих потомков, т.е.

kj > k2j, kj > k2j+1. Допустим, что это условие удалось выполнить для всех j > l. Тогда, проходя только одни путь в дереве с корнем l, можно поместить узел l в надлежащее место. Исходно

условие пирамидальности выполняется для l = N/2 + 1, так как у этого узла дерева нет потомков. Оператор означает целую часть числа.

Рассмотрим на примере процесс приведения дерева к пирамиде. Первоначально дерево

3

Условие пирамидальности выполнено для узла с ключом 8. Теперь уменьшаем l на единицу и попадаем в узел 1. Условие пирамидальности нарушено, следовательно меняем местами с 3. Получаем

1

Снова уменьшаем l на единицу и попадаем в узел 2, меняем его местами со старшим из сыновей. Следующий узел 5. Старший из его сыновей 8. После обмена местами имеем следующее состояние.

1

И наконец, последний узел 7 – корень обменивается местом со старшим из своих потомков и получаем пирамиду

1

Теперь наибольший из ключей находится в вершине. Помещаем его в последнюю позицию таблицы, а весь путь в дереве вдоль старших потомков поднимается наверх.

Алгоритм пирамидальной сортировки следующий. Записи переразмещаются на том же месте. Сначала таблица перестраивается в пирамиду, после чего вершина пирамиды многократно исключается и записывается на свое окончательное место.

Функция, выполняющая сортировку, выглядит следующим образом: void PyramidSort (int *t, int n){

int l, r, k, i, j; l = n/2 +1;

r = n;

while (l > 1 | | r > 1) { if (l > 1) {

l --;

k = t [l-1];

}else {

k = t [r-1];

t [r-1] = t [0]; r --;

if (r = = 1) { t[0] = k; continue;

}

}

j = l;

for (; ;) { i = j;

j = 2*j;

if (j <= r) { if (j < r) {

if (t [j-1] < t [j]) j ++;

}

if (k >= t [j-1]) break; t [i-1] = t [j-1];

} else break;

}

t [i-1] = k;

}

}

Быстрая сортировка Хоара

В библиотеке языка Си имеется функция qsort, выполняющая сортировку методом Хоара. Рассмотрим следующую схему сравнений и обменов. Устанавливаем указатели i и j на

первый и последний элементы последовательности ключей. 5 3 8 6 4 9 2 7

i j

Сравниваем ki и kj и, если обмен не требуется, уменьшим j на единицу, далее повторим процесс сравнения.

5 3 8 6 4 9 2 7 i j