
матан сука
.pdf
1. теорема о существовании точных граней ограниченного множества
Теорема. 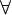 ограниченное сверху непустое числовое множество имеет верхнюю грань, а всякое ограниченное снизу непустое числовое множество имеет нижнюю грань.
ограниченное сверху непустое числовое множество имеет верхнюю грань, а всякое ограниченное снизу непустое числовое множество имеет нижнюю грань.
Доказательство. Пусть |
- ограниченное сверху непустое числовое множество. |
Обозначим |
|||||
через |
множество всех чисел, ограничивающих сверху множество |
. |
|
||||
Множество |
ограничено сверху, поэтому множество |
не пусто. Каждый |
|
||||
элемент |
|
ограничивает сверху множество |
, т.е. |
|
. |
|
|
Элементы |
и являются произвольными элементами соответственно |
множеств |
и , |
||||
поэтому, в силу свойства непрерывности действительных |
|
|
|
||||
чисел, |
|
и |
имеет место неравенство |
. |
|
||
Выполнение неравенства 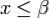 означает, что число
означает, что число 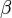 ограничивает сверху множество
ограничивает сверху множество 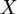 , а выполнение неравенства
, а выполнение неравенства 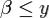 для всех
для всех 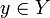 , т.е. для всех чисел, ограничивающих сверху множество
, т.е. для всех чисел, ограничивающих сверху множество 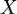 , означает, что число
, означает, что число 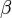 является наименьшим среди всех таких чисел, т.е. верхней гранью множества
является наименьшим среди всех таких чисел, т.е. верхней гранью множества 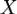 :
:  .
.
 -е верхней грани у ограниченного сверху непустого множества доказано.
-е верхней грани у ограниченного сверху непустого множества доказано.
Если теперь 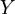 - непустое ограниченное снизу числовое множество, то отнесём к множеству
- непустое ограниченное снизу числовое множество, то отнесём к множеству 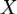 все числа, ограничивающие снизу множество
все числа, ограничивающие снизу множество 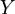 .
.
Аналогично рассмотренному случаю верхней грани, легко убеждаемся, что, в силу свойства неперрывности действительных чисел, 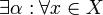 и
и 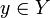 имеет место неравенство
имеет место неравенство 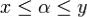 .
.
Это означает, что 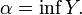 Теорема доказана.
Теорема доказана.
2. леммы о бесконечно малых
Опр. 1: Переменная |
называется бесконечно малой, если её пределом |
является |
нуль. |
ЛЕММА №1: Для того чтобы переменная  имела своим пределом постоянное число a, необходимо и достаточно выполнения равенства:
имела своим пределом постоянное число a, необходимо и достаточно выполнения равенства:
– |
бесконечно |
малая |
величина. |

Результат следует из того, что разность |
есть расстояние от точки |
до |
|
её предела , это расстояние стремится |
к нулю, т. к. |
, и наоборот: |
|
если расстояние стремиться к нулю, то |
. |
|
|
ЛЕММА №2: Алгебраическая |
сумма конечного числа бесконечно малых, |
||||
есть |
величина |
|
бесконечно |
малая. |
|
|
|
Доказательство: |
|
|
|
Рассмотрим, |
например, |
сумму |
3-х |
бесконечно |
малых. |
Возьмем любое E > 0, т. к. |
,то по определению существует |
||||
номер n такой, |
что |
будет |
выполняться |
три |
неравенства: |
|
|
|
|
(по |
лемме №2 о |
|
вещественных |
|
|
числах). |
|
Существует |
номер n, такой, что при n > |
N выполняется неравенство: |
|
|
|
для |
, это и означает, что |
, Ч. Т. Д. |
|
ЛЕММА |
|
№3:Произведение ограниченной переменной на бесконечно |
|
малую есть величина басконечно малая |
|
|||
Пусть |
|
|
|
|
Требуется доказать, что:
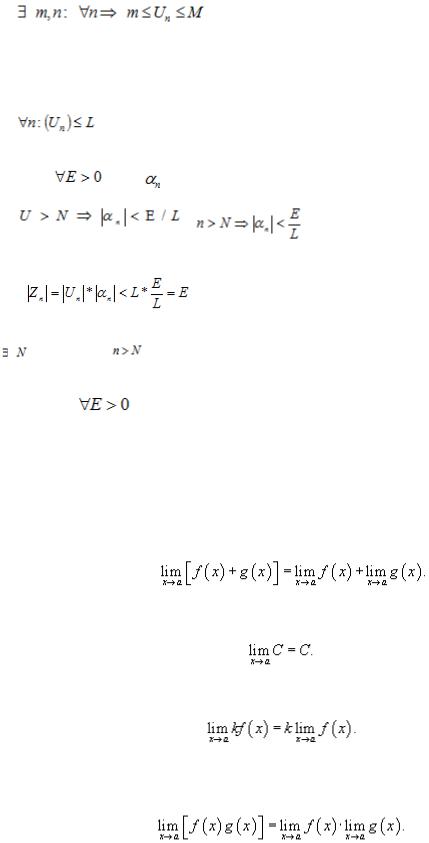
Доказательство:
Пусть 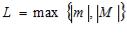
Возьмем |
, т.к. – бесконечно малая, то существует номер N такой что |
при: |
, |
Тогда |
. |
, |
при |
следовательно, |
выполняется |
неравенства: |
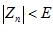 ,
,
Это и означает, что: 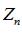 – бесконечно малая.
– бесконечно малая.
3. Арифметические свойства пределов
Предел суммы двух функций равен сумме пределов этих функций:
Предел постоянной величины
Предел постоянной величины равен самой постоянной величине:
Предел произведения функции на постоянную величину
Постоянный коэффициент можно выносить за знак предела:
Предел произведения
Предел произведения двух функций равен произведению пределов этих функций (при условии, что последние существуют):
Предел частного
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

Предел логарифмической функции
где основание a > 0.
4 лемма о вложенных отрезках
Для всякой системы вложенных отрезков
существует хотя бы одна точка  , принадлежащая всем отрезкам данной системы.
, принадлежащая всем отрезкам данной системы.
Если, кроме того, длина отрезков системы стремится к нулю:
то  — единственная общая точка всех отрезков данной системы.
— единственная общая точка всех отрезков данной системы.
1) Существование общей точки. Множество левых концов отрезков |
лежит на числовой |
прямой левее множества правых концов отрезков 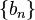 , поскольку
, поскольку
В силу аксиомы непрерывности, существует точка  , разделяющая эти два множества, то есть
, разделяющая эти два множества, то есть
в частности
Последнее неравенство означает, что  — общая точка всех отрезков данной системы.
— общая точка всех отрезков данной системы.
2) Единственность общей точки. Пусть длина отрезков системы стремится к нулю. Покажем, что существует только одна точка, принадлежащая всем отрезкам системы. Предположим противное: пусть имеется две различные точки  и
и  , принадлежащие всем отрезкам системы:
, принадлежащие всем отрезкам системы:
Тогда для всех номеров 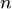 выполняются неравенства:
выполняются неравенства:
В силу условия стремления к нулю длин отрезков для любого |
для всех номеров , начиная |
с некоторого будет выполняться неравенство |
|
Взяв в этом неравенстве |
, получим |
Противоречие. Лемма доказана полностью.
5 Лемма Больцоно-Вейерштрасса

Теорема. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Доказательство. Так как последовательность ограничена, то она имеет хотя бы одну предельную точку x. В таком случае из этой последовательности можно выделить подпоследовательность, сходящуюся к точке x.
Замечание 1. Из любой ограниченной последовательности можно выделить монотонную подпоследовательность.
В самом деле, в силу теоремы Больцано-Вейерштрасса из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность, а из этой подпоследовательности можно выделить монотонную подпоследовательность.
Замечание 2. Пусть {xn} - ограниченная последовательность, элементы которой находятся в сегменте [a, b]. Тогда предел с любой сходящейся
подпоследовательности 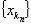 также находится на сегменте [a, b].
также находится на сегменте [a, b].
6 критерий коши
Теорема ( Критерий Коши ). Для того, чтобы последовательноссходилась,ть необходимо достаточно чтобыбылаонафундаментальной.
Доказательство.
Необходимость. Пусть сходится
Достаточность. |
Пусть - фундаментальная |
последовательнос ть. |
Докажем, |
что |
|
ограничена |
. |
|
|
|
|
Так как последовательнос ть |
|
, втокресности |
которой |
|
|
существуютвсе |
элементы |
. |
|
|
|
|
|
|
|
|
|
Положим, |
|
|
. |
|
|
Вотрезке-A][A,содержатся все элементы последовательносограниченнати,т. ..
Вследствие теоремы -БольцаноВейерштрасса () < (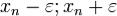 ).
).
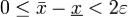 в силу произвольности
в силу произвольности

7 теорема о пределе монотонной последовательности
Определение.
Последовательность {xn} называется монотонно возрастающей, если для любого n xn+1 xn.
Теорема о существовании предела монотонной последовательности.
1. Если |
последовательность {xn} монотонно возрастает (убывает) |
и ограничена |
сверху (снизу), то у нее существует конечный предел, |
равный sup{xn} ( inf{xn} ).
2 Если последовательность {xn} монотонно возрастает (убывает), но сверху (снизу) не ограничена, то у нее существует предел, равный + ( - ).
Теорема:
1.Если последовательность 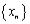 монотонно возрастает и ограниченна сверху, то она сходится к конечному пределу;
монотонно возрастает и ограниченна сверху, то она сходится к конечному пределу;
2.Если последовательность 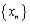 монотонно возрастает, но неограниченна сверху,
монотонно возрастает, но неограниченна сверху,
то 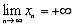 .
.
Доказательство. |
|
|
|
Часть 1. Пусть ограниченны сверху, т.е. |
такое, что |
. Тогда, |
|
согласно теореме о существовании супремума мы можем утверждать, что |
. |
||
Вспомним свойства |
. Их было два |
|
|
1. |
|
|
|
2. |
|
|
|
Но учтем теперь что |
. Это значит, что |
. Тогда имеем следующую |
|
цепочку неравенств |
|
|
|
Выбрасывая лишнее получим, что 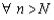
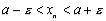 или
или 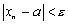 , что и говорит о том, что
, что и говорит о том, что 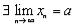 .
.
Заметьте, что предел равен как раз супремуму множества 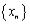 .
.

Часть 2. Пусть теперь 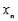 неограниченна сверху. Это значит, что
неограниченна сверху. Это значит, что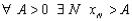 .
.
Но 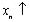 . Значит,
. Значит, 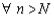
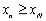 и поэтому можно записать
и поэтому можно записать 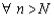
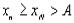 . Выбрасывая в этом неравенстве
. Выбрасывая в этом неравенстве 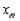 , получим окончательно
, получим окончательно
что и говорит о том, что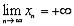 .
.
1 способы задания функции
Различают 4 способа задания фу нкции:
1. т абличный Состоит в простом перечислении элементов фу нкции f, т .е. при эт ом способе у казывается значение аргумента x и соответствующе значение функции y =f(x)
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x1 |
|
x2 |
|
x3 |
|
x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
y1 |
|
y2 |
|
y3 |
|
y4 |
|
|
|
|
|
|
|
|
|
|
|
|
Удобен, когда f --конечное множество, когда же f бесконечное, указывается лишь избранные пары
(х ,у ).
Достоинства: точность, быстрота, по т аблице значений легко найти нужное значение фу нкции.
Недостатки: неполнота, отсутствие наглядности.
2. аналит ический (формулы) Явл яется наиболее важным для МА (мат.анализа), поскольку мет оды МА (дифференциального, интегрального счисления) предполагают этот способ задания.
Одна и т а ж е фу нкция может быть задана различными формулами: y= sin(x) y=√1−
cos2(x) Иногда в разл ичных частях своих областей определяемая функция может быть задана различными формулами f(x)={f1(x),x D1 fn(x),x Dn nk=1Dk=D(f) . Част о при эт ом способе
задания фу нкции область определения не у казывается, т огда под областью определения понимается естественная область определения, т .е. множество всех значений x при кот орых фу нкция принимает действительное значение.
Част ным случаем аналитического способа задания функции является задание фу нкции
у равнением вида F(x,y)=0 (1) Если это у равнение обладает свойством, что x Д сопоставляется единст венное y, т акое, что F(x,y)=0, т о говорят, что уравнение (1) на Д неявно задает фу нкцию.
Еще один част ный случай задания фу нкции -- параметрический, при эт ом каждая пара (x,y) f задает ся с помощью пары фу нкций x=ϕ(t),y=ψ(t) где t M .

3. графический Обл асть определения -- проекция данного графика на Ох , а множ ество значений -- проекция Д(f) на Оу . Применяет ся в медицине, т ехнике.
Достоинство: наглядность.
Недостаток: неточность.
4. словестный От ношение f, по которому каждому х находящееся соответствие у описывается словесно. Например, y =[x] : x из R (Целой частью х из R называют любое целое число не превосходящее х).
Достоинство: можно воспользоваться когда первые т ри не срабатывают.
Недостаток: ненаглядность.
2 основные элементарные функции
Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий
Алгебраическая функция — элементарная функция, которая в окрестности каждой точки области определения может быть неявно задана с помощью алгебраического уравнения.
У=ф(х)
тепенная функция — функция |
, где (показатель степени) — |
|
некоторое вещественное число[1]. К степенным часто относят и функцию вида |
, |
|
где k — некоторый масштабный множитель |
|
|
Рациональная функция — функцию вида y = P(x) / Q(x), где P(x) и Q(x) – многочлены, степени выше первой.
Показательная функция — математическая функция 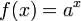 , где
, где 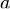 называется основанием степени, а
называется основанием степени, а 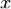 — показателем степени.
— показателем степени.
Логарифмическая функция
Тригонометрические функции
3 предел функции в точке. Определение гейне.
Предел функции в заданной точке — такая величина, к которой стремится функция при стремлении её аргумента к данной точке.
Определение предела по Гейне. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой
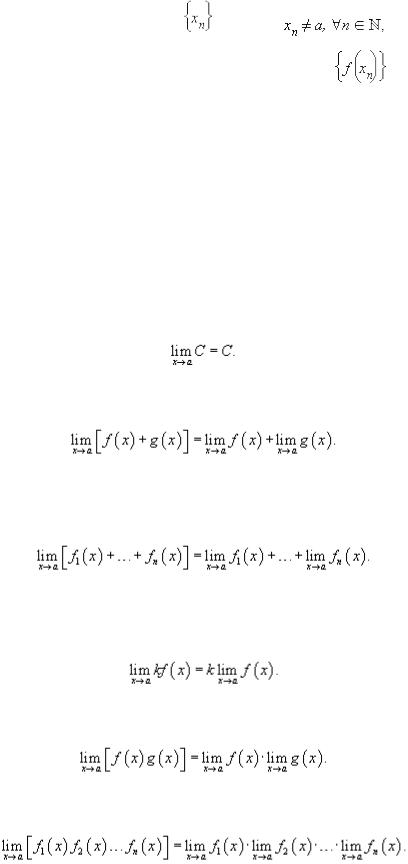
точки a, и для любой последовательности |
такой, что |
сходящейся к |
числу a, соответствующая последовательность значений функции |
сходится к числу A. |
|
4 предел функции в точке. Определение коши
Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0существует δ > 0 такое, что для всех x, удовлетворяющих
условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.
5 предел функции в точке. Основные свойства
1) Предел постоянной величины
Предел постоянной величины равен самой постоянной величине:
2) Предел суммы
Предел суммы двух функций равен сумме пределов этих функций:
Аналогично предел разности двух функций равен разности пределов этих функций.
Расширенное свойство предела суммы:
Предел суммы нескольких функций равен сумме пределов этих функций:
Аналогично предел разности нескольких функций равен разности пределов этих функций.
3) Предел произведения функции на постоянную величину
Постоянный коэффициэнт можно выносить за знак предела:
4) Предел произведения
Предел произведения двух функций равен произведению пределов этих функций:
Расширенное свойство предела произведения
Предел произведения нескольких функций равен произведению пре делов этих функций:
5) Предел частного
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
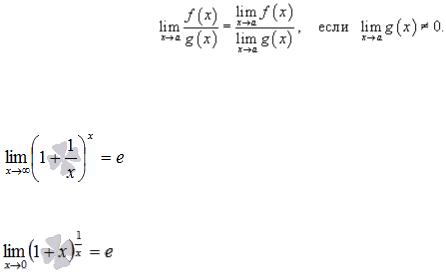
6 второй замечательный предел
Второй замечательный предел имеет вид:
или в другой записи
В случае второго замечательного предела имеем дело с неопределенностью вида единица в степени бесконечность  .
.
7 Теорема о пределе монотонной функции.
Предел монотонной функции
Определение. Функция 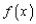 называется
называется
-монотонно возрастающей, если из 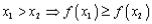
-строго монотонно возрастающей, если из 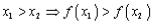
-монотонно убывающей, если из 
-строго монотонно убывающей, если из  .
.
Докажем одну из возможных здесь теорем.
Теорема. Если  монотонно возрастает и ограниченна сверху при
монотонно возрастает и ограниченна сверху при 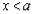 , то существует конечный предел слева
, то существует конечный предел слева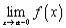 .
.
Доказательство. Рассмотрим множество 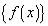 значений функции
значений функции 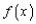 при
при . По
. По
условию теоремы, это множество ограниченно сверху, т.е. 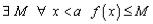 . По теореме о существовании супремума отсюда следует, что существует
. По теореме о существовании супремума отсюда следует, что существует
конечный 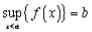 .
.
Покажем, что 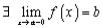 . По свойствам супремума
. По свойствам супремума
